要深入了解正則表達式,必須首先理解有窮自動機。
有窮自動機(Finite Automate)是用來模擬實物系統的數學模型,它包括如下五個部分:
- 有窮狀態集States
- 輸入字符集Input symbols
- 轉移函數Transitions
- 起始狀態Start state
- 接受狀態Accepting state(s)
下圖為一臺有窮自動機
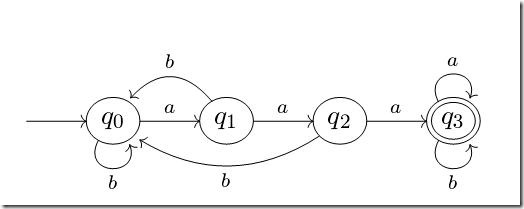
可以看到,該自動機包含四個狀態q0, q1, q2, q3,兩個輸入字符a, b,轉移函數如圖所示,起始狀態為q0,接受狀態為q3。
有窮自動機,按照轉移函數的不同,又可分為確定型有窮自動機(Determinism Finite Automate, DFA),與非確定型有窮自動機(Non-determinism Finite Automate, NFA)。
非確定有窮自動機容許轉移函數不確定,換句話說,對任意狀態,輸入任意一個字符,可以轉移到0個,1個或者多個狀態。
下圖是一臺非確定有窮自動機,可以看到,對狀態q0輸入字符a,既可以轉移到q0,也可以轉移到q1,這就是“非確定”的意義所在。
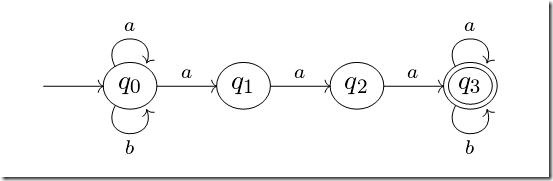
對某個自動機來說,如果從起始狀態,接受一系列輸入字符,可以轉移到接受狀態,即認為這一系列字符可以被自動機接受。
如果兩臺自動機能夠接受的輸入字符串(或者叫做“正則語言”Regular Language)完全相同,則這兩臺自動機是等價的。
可以證明,對于每一個非確定有窮自動機,都存在與之等價的確定型有窮自動機(證明略)。
正則表達式就是建立在自動機的理論基礎上的:用戶寫完正則表達式之后,正則引擎會按照這個表達式構建相應的自動機(可能是NFA,也可能是DFA,但它們必定是等價的),若輸入一串文本之后,自動機抵達了接受狀態,則這串文本可以“匹配”用戶指定的正則表達式。
下面是同一個正則表達式 a|ab 對應的NFA和DFA
NFA
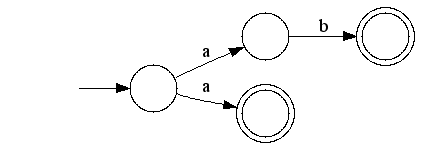
DFA

在Mastering Regular Expression中,Friedl首先分析了NFA和DFA的區別,DFA比較快,但不提供Backtrack(回溯)功能,NFA比較慢,但提供了Backtrack功能。
在分析兩種引擎的匹配過程時,Friedl指出,NFA是基于表達式的(Regex-Directed),而DFA是基于文本的(Text-Directed)。
舉例來說,對于正則表達式 to(nite|knight|night),NFA在匹配最開始兩個字符(to)之后,剩下的三個組件(component)是 nite, knight 和 night,于是正則引擎會依次嘗試這三個選擇分支(每次嘗試一個);而DFA在匹配最開始兩個字符之后,會將剩下的三個選擇拆分作字符,并行嘗試,也就是說,匹配 to 之后,先匹配 k 或者 n ,如果 k 不能匹配,則放棄 knigth 所在的分支,再匹配 i ,再匹配 t 或 g ……這樣繼續下去,直到匹配結束。
不幸的是,Friedl對匹配過程的分析,是完全錯誤的——引擎的不同,是指構建的自動機的不同,而不是匹配算法的不同!
DFA引擎在任意時刻必定處于某個確定的狀態,而NFA引擎可能處于一組狀態之中的任何一個,所以,NFA引擎必須記錄所有的可能路徑(trace multiple possible routes through the NFA),NFA之所以能夠提供Backtrack的功能,原因就在這里。
傳統的NFA匹配算法是帶回溯的深度優先搜索(backtracking depth-first search,就是上文所說的Regex-Based過程),而新的PCRE算法提供了效率更高的廣度優先搜索,可以同時保持所有可能的NFA狀態(請參考http://www.cl.cam.ac.uk/Teaching/current/RLFA/,尤其是Lecture Notes的section 2.2)。
Friedl的錯誤就在這里,他混淆了應用PCRE算法的NFA與DFA的匹配過程。
需要指出的是,即使應用PCRE算法,NFA的速度仍然低于DFA,這是由NFA需要同時保存多種可能的性質決定的。從理論上說,如果我們不需要應用 Backtrack,完全可以從NFA構造出等價的DFA,再進行匹配,這樣能大大提高速度——代價是,DFA需要更多的空間。