一般來說,方陣能描述任意線性變換。線性變換保留了直線和平行線,但原點沒有移動。線性變換保留直線的同時,其他的幾何性質如長度、角度、面積和體積可能被變換改變了。從非技術意義上說,線性變換可能“拉伸”坐標系,但不會“彎曲”或“卷折”坐標系。
矩陣是怎樣變換向量的
向量在幾何上能被解釋成一系列與軸平行的位移,一般來說,任意向量v都能寫成“擴展”形式:

另一種略有差別的形式為:
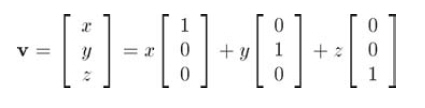
注意右邊的單位向量就是x,y,z軸,這里只是將概念數學化,向量的每個坐標都表明了平行于相應坐標軸的有向位移。
讓我們將上面的向量和重寫一遍,這次分別將p、q、r定義為指向+x,+y和+z方向的單位向量,如下所示:
v = xp + yq + zr
現在,向量v就被表示成向量p,q,r的線性變換了,向量p,q,r稱作基向量。這里基向量是笛卡爾坐標軸,但事實上,一個坐標系能用任意3個基向量定義,當然這三個基向量要線性無關(也就是不在同一平面上)。以p、q、r為行構建一個3
x 3矩陣M,可得到如下矩陣:
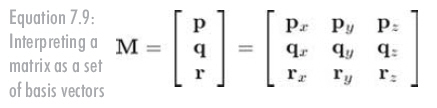
用一個向量乘以該矩陣,得到:
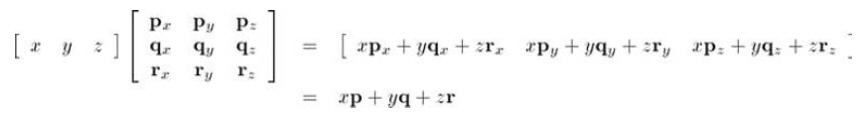
如果把矩陣的行解釋為坐標系的基向量,那么乘以該矩陣就相當于執行了一次坐標轉換,如果aM=b,我們就可以說,M將a轉換到b。
從這點看,術語“轉換”和“乘法”是等價的。
坦率地說,矩陣并不神秘,它只是用一種緊湊的方式來表達坐標轉換所需的數學運算。進一步,用線性代數操作矩陣,是一種進行簡單轉換或導出更復雜轉換的簡便方法。
矩陣的形式:
基向量[1, 0, 0], [0, 1, 0], [0, 0, 1]乘以任意矩陣M:
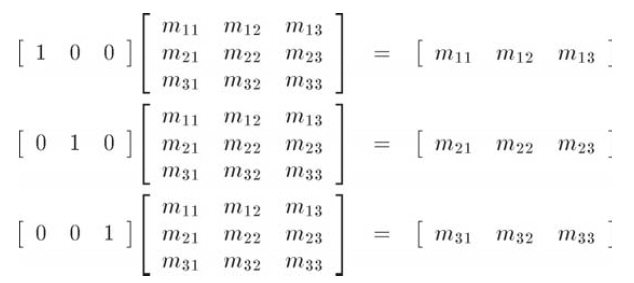
用基向量[1, 0, 0]乘以M時,結果是M的第1行。其他兩行也有同樣的結果,這是一個關鍵的發現:矩陣的每一行都能解釋為轉換后的基向量。
這個強有力的概念有兩條重要性質:
1、有了一種簡單的方法來形象化解釋矩陣所代表的變換。
2、有了反向建立矩陣的可能 ----
給出一個期望的變換(如旋轉、縮放等),能夠構造一個矩陣代表此變換。我們所要做的一切就是計算基向量的變換,然后將變換后的基向量填入矩陣。
首先來看看2D例子,一個2 x 2矩陣:

這個矩陣代表的變換是什么?首先,從矩陣中抽出基向量p和q:
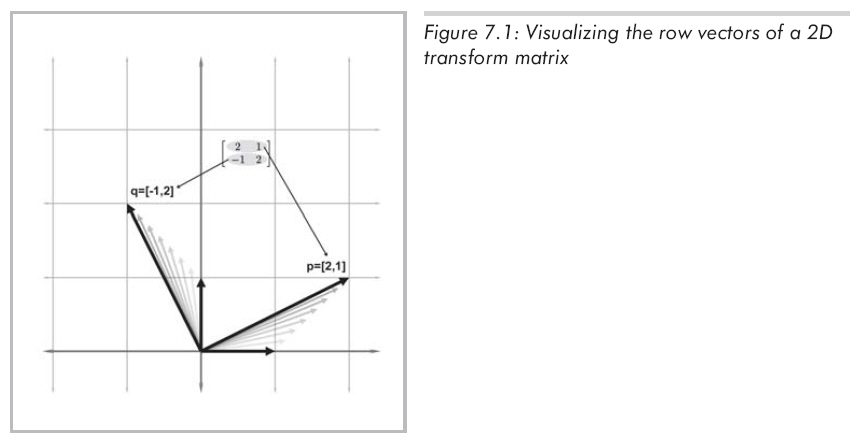
p = [2 1]
q = [-1 2]
圖7.1以“原”基向量(x軸,y軸)為參考,在笛卡爾平面中展示了這些向量。
 、
、
如圖7.1所示,x基向量變換至上面的p向量,y基向量變換至q向量。所以2D中想象矩陣的方法就是想象由行向量構成的“L”形狀。這個例子中,能夠很清楚的看到,M代表的部分變換是逆時針旋轉26度。
當然,所有向量都被線性變換所影響,不只是基向量,從“L”形狀能夠得到變換最直觀的印象,把基向量構成的整個2D平行四邊形畫完整有助于進一步看到變換對其他向量的影響,如圖7.2所示:

平行四邊形稱作“偏轉盒”,在盒子中畫一個物體有助于理解,如圖 7.3
所示:
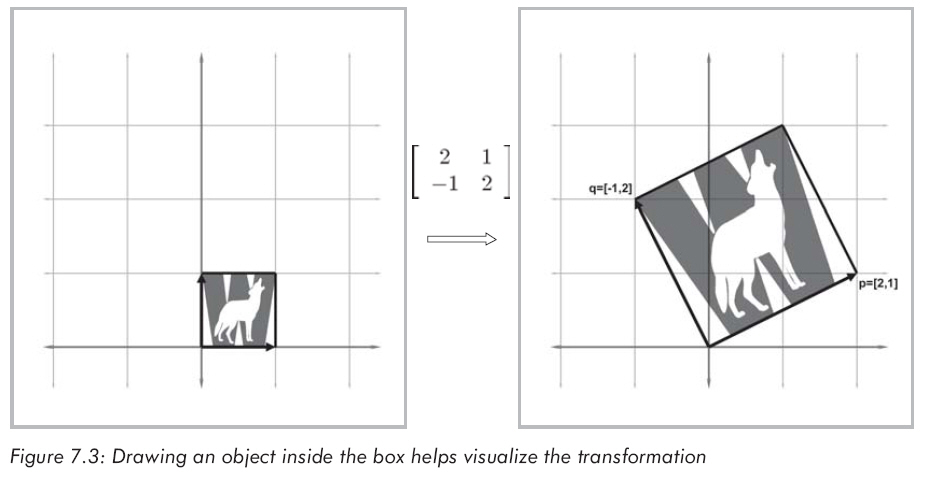
很明顯,矩陣M不僅旋轉坐標系,還會拉伸它。
這種技術也能應用到3D轉換中。2D中有兩個基向量,構成"L"型;3D中有三個基向量,它們形成一個”三腳架“。首先,讓我們展示出一個轉換前的物品。圖7.4展示了一個茶壺,一個立方體。基向量在”單位“向量處。

(為了不使圖形混亂,沒有標出z軸基向量[0, 0, 1],它被茶壺和立方體擋住了。)
現在,考慮以下3D變換矩陣:

從矩陣的行中抽出基向量,能想象出該矩陣所代表的變換。變換后的基向量、立方體、茶壺如圖7.5所示:

這個變換包含z軸順時針旋轉45度和不規則縮放,使得茶壺比以前”高“。注意,變換并沒有影響到z軸,因為矩陣的第三行是[0,
0 , 1]。