矩陣是3D數(shù)學(xué)的重要基礎(chǔ)，它主要用來描述兩個(gè)坐標(biāo)系間的關(guān)系，通過定義一種運(yùn)算而將一個(gè)坐標(biāo)系中的向量轉(zhuǎn)換到另一個(gè)坐標(biāo)系中。在線性代數(shù)中，矩陣就是以行和列形式組織的矩形數(shù)字塊，向量是標(biāo)量的數(shù)組，矩陣是向量的數(shù)組。

矩陣的維度和記法

矩陣的維度被定義為它包含了多少行多少列，一個(gè) r x c 矩陣有r行c列。用黑體大寫字母表示矩陣，如：M、A、R。需要引用矩陣的分量時(shí)，采用下標(biāo)法，常使用對應(yīng)的斜體小寫字母，如下面的3 x 3矩陣所示：

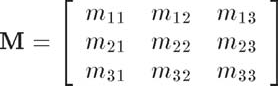
方陣

行數(shù)和列數(shù)相同的矩陣稱作方陣，方陣的對角線元素就是方陣中行號和列號相同的元素。其他元素均為非對角元素，簡單的說，方陣的對角元素就是方陣對角線上的元素。

如果所有非對角元素都為0，那么稱這種矩陣為對角矩陣。單位矩陣是一種特殊的對角矩陣，n維單位矩陣記作In，是nxn矩陣，對角線元素為1，其他元素為0.

單位矩陣非常特殊，因?yàn)樗蔷仃嚨某朔▎挝辉Ｆ浠拘再|(zhì)是用任意一個(gè)矩陣乘以單位矩陣，都將得到原矩陣。所以在某種意義上，單位矩陣對矩陣的作用就猶如1對于標(biāo)量的作用。

向量作為矩陣使用

矩陣的行數(shù)和列數(shù)可以是任意正整數(shù)，當(dāng)然也包括1。一個(gè)n維向量能被當(dāng)作 1 x n 矩陣或 n x 1 矩陣。1 x n 矩陣稱作行向量，n x 1 矩陣稱作列向量。行向量平著寫，列向量豎著寫。

轉(zhuǎn)置

考慮一個(gè) r x c 矩陣M，M的轉(zhuǎn)置記作MT，是一個(gè) c x r 矩陣，它的列由M的行組成，可以從另一方面理解，即沿著矩陣的對角線翻折。

對于向量來說，轉(zhuǎn)置將使行向量變成列向量，使列向量成為行向量，見公式7.3：

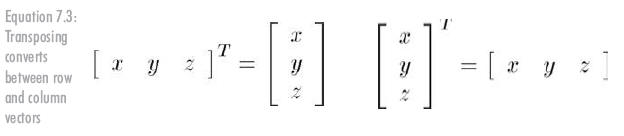
標(biāo)量和矩陣的乘法

矩陣M能和標(biāo)量k相乘，結(jié)果是一個(gè)和M維數(shù)相同的矩陣。矩陣和標(biāo)量相乘的記法如公式7.4所示，標(biāo)量經(jīng)常寫在左邊，不需要寫乘號。這種乘法法則很直觀，即用k乘以M中的每個(gè)元素。

矩陣乘法

某些情況下，兩個(gè)矩陣能夠相乘，決定矩陣能否相乘以及怎樣計(jì)算結(jié)果的法則初看起來有些奇怪。一個(gè)r x n矩陣A能夠乘以一個(gè)n x c矩陣B，結(jié)果是一個(gè)r x c矩陣，記作AB。

例如，設(shè)A為4 x 2矩陣，B為2 x 5矩陣，那么結(jié)果AB為4 x 5矩陣：

如果矩陣A的列數(shù)和B的行數(shù)不匹配，則乘法AB無意義。

矩陣乘法計(jì)算如下：記r x n矩陣A與n x c矩陣B的積r x c矩陣AB為C。C的任意元素Cij等于A的第i行向量與B的第j列向量的點(diǎn)乘結(jié)果。

正式定義為：