Description
Centuries ago, King Arthur and the Knights of the Round Table used to meet every year on New Year's Day to celebrate their fellowship. In remembrance of these events, we consider a board game for one player, on which one king and several knight pieces are placed at random on distinct squares.
The Board is an 8x8 array of squares. The King can move to any adjacent square, as shown in Figure 2, as long as it does not fall off the board. A Knight can jump as shown in Figure 3, as long as it does not fall off the board.
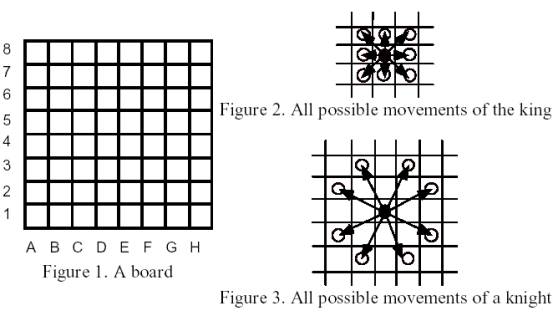
During the play, the player can place more than one piece in the same square. The board squares are assumed big enough so that a piece is never an obstacle for other piece to move freely.
The player抯 goal is to move the pieces so as to gather them all in the same square, in the smallest possible number of moves. To achieve this, he must move the pieces as prescribed above. Additionally, whenever the king and one or more knights are placed in the same square, the player may choose to move the king and one of the knights together henceforth, as a single knight, up to the final gathering point. Moving the knight together with the king counts as a single move.
Write a program to compute the minimum number of moves the player must perform to produce the gathering.
Input
Your program is to read from standard input. The input contains the initial board configuration, encoded as a character string. The string contains a sequence of up to 64 distinct board positions, being the first one the position of the king and the remaining ones those of the knights. Each position is a letter-digit pair. The letter indicates the horizontal board coordinate, the digit indicates the vertical board coordinate.
0 <= number of knights <= 63
Output
Your program is to write to standard output. The output must contain a single line with an integer indicating the minimum number of moves the player must perform to produce the gathering.
Sample Input
D4A3A8H1H8
Sample Output
10
Source
棋盤上有1個(gè)國王和若干個(gè)騎士，要把國王和每個(gè)騎士移動(dòng)到同一個(gè)格子內(nèi)，問需要移動(dòng)的最小步數(shù)是多少。如果國王和騎士走到同一個(gè)格子里，可以由騎士帶著國王一起移動(dòng)。
枚舉棋盤上的64個(gè)點(diǎn)作為終點(diǎn)，對(duì)于每一個(gè)假定的終點(diǎn)，再枚舉這64個(gè)點(diǎn)作為國王和某個(gè)騎士相遇的點(diǎn)，最后求出需要移動(dòng)的最小步數(shù)。其中根據(jù)騎士和國王移動(dòng)的特點(diǎn)可以預(yù)處理出從1個(gè)點(diǎn)到另外1個(gè)點(diǎn)所需的最小移動(dòng)次數(shù)，也可用搜索。
#include <iostream>
using namespace std;
const int inf = 100000;
char str[150];
int k[64],king[64][64],knight[64][64];
int move1[8][2]=
{-1,-1,-1,0,-1,1,0,1,1,1,1,0,1,-1,0,-1};
int move2[8][2]={-1,-2,-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2};
void init(){
int i,j,x,y,tx,ty;
for(i=0;i<64;i++)
for(j=0;j<64;j++)
if(i==j) king[i][j]=knight[i][j]=0;
else king[i][j]=knight[i][j]=inf;
for(i=0;i<64;i++){
x=i/8,y=i%8;
for(j=0;j<8;j++){
tx=x+move1[j][0],ty=y+move1[j][1];
if(tx>=0 && ty>=0 && tx<8 && ty<8)
king[i][8*tx+ty]=1;
}
}
for(i=0;i<64;i++){
x=i/8,y=i%8;
for(j=0;j<8;j++){
tx=x+move2[j][0],ty=y+move2[j][1];
if(tx>=0 && ty>=0 && tx<8 && ty<8)
knight[i][8*tx+ty]=1;
}
}
}
void floyd1(){
int i,j,k;
for(k=0;k<64;k++)
for(i=0;i<64;i++)
for(j=0;j<64;j++)
if(king[i][k]+king[k][j]<king[i][j])
king[i][j]=king[i][k]+king[k][j];
}
void floyd2(){
int i,j,k;
for(k=0;k<64;k++)
for(i=0;i<64;i++)
for(j=0;j<64;j++)
if(knight[i][k]+knight[k][j]<knight[i][j])
knight[i][j]=knight[i][k]+knight[k][j];
}
int main(){
int i,j,l,cnt,pos,sum,ans,len,t1,t2;
init();
floyd1();
floyd2();
while(scanf("%s",str)!=EOF){
len=strlen(str);
pos=(str[0]-'A')+(str[1]-'1')*8;
cnt=(len-2)/2;
if(cnt==0){
printf("0\n");
continue;
}
for(i=0,j=2;i<cnt;i++,j+=2)
k[i]=(str[j]-'A')+(str[j+1]-'1')*8;
for(ans=inf,i=0;i<64;i++){
for(sum=l=0;l<cnt;l++)
sum+=knight[k[l]][i];
for(j=0;j<64;j++){
t1=king[pos][j];
for(t2=inf,l=0;l<cnt;l++)
t2=min(t2,knight[k[l]][j]+knight[j][i]-knight[k[l]][i]);
ans=min(ans,sum+t1+t2);
}
}
printf("%d\n",ans);
}
return 0;
}