mysileng

                    程序員編程藝術：第三章、尋找最小的k個數

作者：July。
時間：二零一一年四月二十八日。
致謝：litaoye， strugglever，yansha，luuillu，Sorehead，及狂想曲創作組。
微博：http://weibo.com/julyweibo。
出處：http://blog.csdn.net/v_JULY_v。
----------------------------------

前奏 
    @July_____：1、當年明月：“我寫文章有個習慣，由于早年讀了太多學究書，所以很痛恨那些故作高深的文章，其實歷史本身很精彩，所有的歷史都可以寫得很好看，...。”2、IT技術文章，亦是如此，可以寫得很通俗，很有趣，而非故作高深。希望，我可以做到。

    下面，我試圖用最清晰易懂，最易令人理解的思維或方式闡述有關尋找最小的k個數這個問題（這幾天一直在想，除了計數排序外，這題到底還有沒有其它的O（n）的算法? ）。希望，有任何問題，歡迎不吝指正。謝謝。

尋找最小的k個數
題目描述：5.查找最小的k個元素
題目：輸入n個整數，輸出其中最小的k個。
例如輸入1，2，3，4，5，6，7和8這8個數字，則最小的4個數字為1，2，3和4。

第一節、各種思路，各種選擇

• 0、   咱們先簡單的理解，要求一個序列中最小的k個數，按照慣有的思維方式，很簡單，先對這個序列從小到大排序，然后輸出前面的最小的k個數即可。
• 1、   至于選取什么的排序方法，我想你可能會第一時間想到快速排序，我們知道，快速排序平均所費時間為n*logn，然后再遍歷序列中前k個元素輸出，即可，總的時間復雜度為O（n*logn+k）=O（n*logn）。
• 2、   咱們再進一步想想，題目并沒有要求要查找的k個數，甚至后n-k個數是有序的，既然如此，咱們又何必對所有的n個數都進行排序列?
         這時，咱們想到了用選擇或交換排序，即遍歷n個數，先把最先遍歷到得k個數存入大小為k的數組之中，對這k個數，利用選擇或交換排序，找到k個數中的最大數kmax（kmax設為k個元素的數組中最大元素），用時O（k）（你應該知道，插入或選擇排序查找操作需要O（k）的時間），后再繼續遍歷后n-k個數，x與kmax比較：如果x<kmax，則x代替kmax，并再次重新找出k個元素的數組中最大元素kmax‘（多謝kk791159796 提醒修正）；如果x>kmax，則不更新數組。這樣，每次更新或不更新數組的所用的時間為O（k）或O（0），整趟下來，總的時間復雜度平均下來為：n*O（k）=O（n*k）。
• 3、   當然，更好的辦法是維護k個元素的最大堆，原理與上述第2個方案一致，即用容量為k的最大堆存儲最先遍歷到的k個數，并假設它們即是最小的k個數，建堆費時O（k）后，有k1<k2<...<kmax（kmax設為大頂堆中最大元素）。繼續遍歷數列，每次遍歷一個元素x，與堆頂元素比較，x<kmax，更新堆（用時logk），否則不更新堆。這樣下來，總費時O（k+（n-k）*logk）=O（n*logk）。此方法得益于在堆中，查找等各項操作時間復雜度均為logk（不然，就如上述思路2所述：直接用數組也可以找出前k個小的元素，用時O（n*k））。
• 4、 按編程之美第141頁上解法二的所述，類似快速排序的劃分方法，N個數存儲在數組S中，再從數組中隨機選取一個數X（隨機選取樞紐元，可做到線性期望時間O（N）的復雜度，在第二節論述），把數組劃分為Sa和Sb倆部分，Sa<=X<=Sb，如果要查找的k個元素小于Sa的元素個數，則返回Sa中較小的k個元素，否則返回Sa中k個小的元素+Sb中小的k-|Sa|個元素。像上述過程一樣，這個運用類似快速排序的partition的快速選擇SELECT算法尋找最小的k個元素，在最壞情況下亦能做到O（N）的復雜度。不過值得一提的是，這個快速選擇SELECT算法是選取數組中“中位數的中位數”作為樞紐元，而非隨機選取樞紐元。
• 5、   RANDOMIZED-SELECT，每次都是隨機選取數列中的一個元素作為主元，在0（n）的時間內找到第k小的元素，然后遍歷輸出前面的k個小的元素。 如果能的話，那么總的時間復雜度為線性期望時間：O（n+k）=O（n）（當k比較小時）。

         Ok，稍后第二節中，我會具體給出RANDOMIZED-SELECT(A, p, r, i)的整體完整偽碼。在此之前，要明確一個問題：我們通常所熟知的快速排序是以固定的第一個或最后一個元素作為主元，每次遞歸劃分都是不均等的，最后的平均時間復雜度為：O（n*logn）,但RANDOMIZED-SELECT與普通的快速排序不同的是，每次遞歸都是隨機選擇序列從第一個到最后一個元素中任一一個作為主元。

• 6、   線性時間的排序，即計數排序，時間復雜度雖能達到O（n），但限制條件太多，不常用。
• 7、   updated： huaye502在本文的評論下指出：“可以用最小堆初始化數組，然后取這個優先隊列前k個值。復雜度O(n)+k*O(log n)”。huaye502的意思是針對整個數組序列建最小堆，建堆所用時間為O（n）（算法導論一書上第6章第6.3節已經論證，在線性時間內，能將一個無序的數組建成一個最小堆），然后取堆中的前k個數，總的時間復雜度即為：O（n+k*logn）。

    關于上述第7點思路的繼續闡述：至于思路7的O（n+k*logn）是否小于上述思路3的O（n*logk），即O（n+k*logn）?< O（n*logk）。粗略數學證明可參看如下第一幅圖，我們可以這么解決：當k是常數，n趨向于無窮大時，求（n*logk）/（n+k*logn）的極限T，如果T>1，那么可得O（n*logk）>O（n+k*logn），也就是O（n+k*logn）< O（n*logk）。雖然這有違我們慣常的思維，然事實最終證明的確如此，這個極值T=logk>1，即采取建立n個元素的最小堆后取其前k個數的方法的復雜度小于采取常規的建立k個元素最大堆后通過比較尋找最小的k個數的方法的復雜度。但，最重要的是，如果建立n個元素的最小堆的話，那么其空間復雜度勢必為O（N），而建立k個元素的最大堆的空間復雜度為O（k）。所以，綜合考慮，我們一般還是選擇用建立k個元素的最大堆的方法解決此類尋找最小的k個數的問題。

    也可以如gbb21所述粗略證明：要證原式k+n*logk-n-k*logn>0，等價于證（logk-1）n-k*logn+k>0。當when n -> +/inf（n趨向于正無窮大）時，logk-1-0-0>0，即只要滿足logk-1>0即可。原式得證。即O（k+n*logk）>O（n+k*logn） =>O（n+k*logn）< O（n*logk），與上面得到的結論一致。

    事實上，是建立最大堆還是建立最小堆，其實際的程序運行時間相差并不大，運行時間都在一個數量級上。因為后續，我們還專門寫了個程序進行測試，即針對1000w的數據尋找其中最小的k個數的問題，采取兩種實現，一是采取常規的建立k個元素最大堆后通過比較尋找最小的k個數的方案，一是采取建立n個元素的最小堆，然后取其前k個數的方法，發現兩相比較，運行時間實際上相差無幾。結果可看下面的第二幅圖。

  

• 8、   @lingyun310：與上述思路7類似，不同的是在對元素數組原地建最小堆O(n)后，然后提取K次，但是每次提取時，換到頂部的元素只需要下移頂多k次就足夠了，下移次數逐次減少（而上述思路7每次提取都需要logn，所以提取k次，思路7需要k*logn。而本思路8只需要K^2）。此種方法的復雜度為O(n+k^2)。@July：對于這個O（n+k^2）的復雜度，我相當懷疑。因為據我所知，n個元素的堆，堆中任何一項操作的復雜度皆為logn，所以按理說，lingyun310方法的復雜度應該跟下述思路8一樣，也為O（n+k*logn），而非O（n+k*k）。ok，先放到這，待時間考證。06.02。

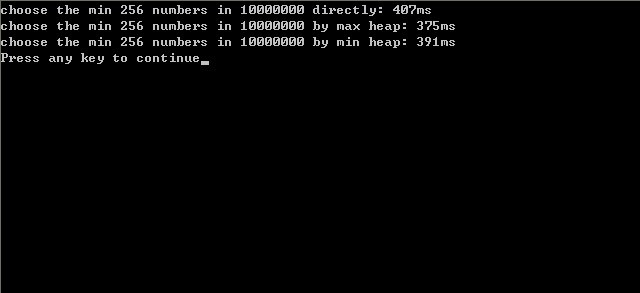
updated：
   經過和幾個朋友的討論，已經證實，上述思路7lingyun310所述的思路應該是完全可以的。下面，我來具體解釋下他的這種方法。

    我們知道，n個元素的最小堆中，可以先取出堆頂元素得到我們第1小的元素，然后把堆中最后一個元素（較大的元素）上移至堆頂，成為新的堆頂元素（取出堆頂元素之后，把堆中下面的最后一個元素送到堆頂的過程可以參考下面的第一幅圖。至于為什么是怎么做，為什么是把最后一個元素送到堆頂成為堆頂元素，而不是把原來堆頂元素的兒子送到堆頂呢?具體原因可參考相關書籍）。

    此時，堆的性質已經被破壞了，所以此后要調整堆。怎么調整呢?就是一般人所說的針對新的堆頂元素shiftdown，逐步下移（因為新的堆頂元素由最后一個元素而來，比較大嘛，既然是最小堆，當然大的元素就要下沉到堆的下部了）。下沉多少步呢?即如lingyun310所說的，下沉k次就足夠了。

    下移k次之后，此時的堆頂元素已經是我們要找的第2小的元素。然后，取出這個第2小的元素（堆頂元素），再次把堆中的最后一個元素送到堆頂，又經過k-1次下移之后（此后下移次數逐步減少，k-2，k-3,...k=0后算法中斷）....，如此重復k-1趟操作，不斷取出的堆頂元素即是我們要找的最小的k個數。雖然上述算法中斷后整個堆已經不是最小堆了，但是求得的k個最小元素已經滿足我們題目所要求的了，就是說已經找到了最小的k個數，那么其它的咱們不管了。

    我可以再舉一個形象易懂的例子。你可以想象在一個水桶中，有很多的氣泡，這些氣泡從上到下，總體的趨勢是逐漸增大的，但卻不是嚴格的逐次大（正好這也符合最小堆的性質）。ok，現在我們取出第一個氣泡，那這個氣泡一定是水桶中所有氣泡中最小的，把它取出來，然后把最下面的那個大氣泡（但不一定是最大的氣泡）移到最上面去，此時違反了氣泡從上到下總體上逐步變大的趨勢，所以，要把這個大氣泡往下沉，下沉到哪個位置呢?就是下沉k次。下沉k次后，最上面的氣泡已經肯定是最小的氣泡了，把他再次取出。然后又將最下面最后的那個氣泡移至最上面，移到最上面后，再次讓它逐次下沉，下沉k-1次...，如此循環往復，最終取到最小的k個氣泡。

    ok，所以，上面方法所述的過程，更進一步來說，其實是第一趟調整保持第0層到第k層是最小堆，第二趟調整保持第0層到第k-1層是最小堆...，依次類推。但這個思路只是下述思路8中正規的最小堆算法（因為它最終對全部元素都進行了調整，算法結束后，整個堆還是一個最小堆）的調優，時間復雜度O（n+k^2）沒有量級的提高，空間復雜度為O（N）也不會減少。

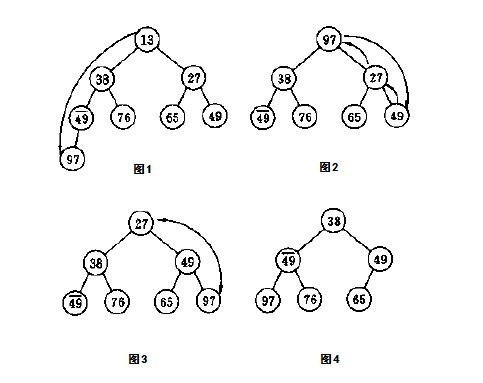
原理理解透了，那么寫代碼，就不難了，完整粗略代碼如下（有問題煩請批評指正）：

    在算法導論第6章有下面這樣一張圖，因為開始時曾一直糾結過這個問題，“取出堆頂元素之后，把堆中下面的最后一個元素送到堆頂”。因為算法導論上下面這張圖給了我一個假象，從a）->b）中，讓我誤以為是取出堆頂元素之后，是把原來堆頂元素的兒子送到堆頂。而事實上不是這樣的。因為在下面的圖中，16被刪除后，堆中最后一個元素1代替16成為根結點，然后1下沉（注意下圖所示的過程是最大堆的堆排序過程，不再是上面的最小堆了，所以小的元素當然要下移），14上移到堆頂。所以，圖中小圖圖b）是已經在小圖a）之和被調整過的最大堆了，只是調整了logn次，非上面所述的k次。

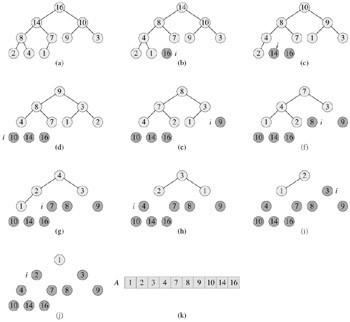
     ok，接下來，咱們再著重分析下上述思路4。或許，你不會相信上述思路4的觀點，但我馬上將用事實來論證我的觀點。這幾天，我一直在想，也一直在找資料查找類似快速排序的partition過程的分治算法（即上述在編程之美上提到的第4點思路），是否能做到O（N）的論述或證明，

     然找了三天，不但在算法導論上找到了RANDOMIZED-SELECT，在平均情況下為線性期望時間O（N）的論證（請參考本文第二節），還在mark allen weiss所著的數據結構與算法分析--c語言描述一書（還得多謝朋友sheguang提醒）中，第7章第7.7.6節（本文下面的第4節末，也有關此問題的闡述）也找到了在最壞情況下，為線性時間O（N）（是的，不含期望，是最壞情況下為O（N））的快速選擇算法（此算法，本文文末，也有闡述），請看下述文字（括號里的中文解釋為本人添加）：

    Quicksort can be modified to solve the selection problem, which we have seen in chapters 1 and 6. Recall that by using a priority queue, we can find the kth largest (or smallest) element in O(n + k log n)（即上述思路7）. For the special case of finding the median, this gives an O(n log n) algorithm.

    Since we can sort the file in O(nlog n) time, one might expect to obtain a better time bound for selection. The algorithm we present to find the kth smallest element in a set S is almost identical to quicksort. In fact, the first three steps are the same. We will call     this algorithm quickselect（叫做快速選擇）. Let |Si| denote the number of elements in Si（令|Si|為Si中元素的個數）. The steps of quickselect are（快速選擇，即上述編程之美一書上的，思路4，步驟如下）:

    1. If |S| = 1, then k = 1 and return the elements in S as the answer. If a cutoff for small files is being used and |S| <=CUTOFF, then sort S and return the kth smallest element.
    2. Pick a pivot element, v (- S.（選取一個樞紐元v屬于S）
    3. Partition S - {v} into S1 and S2, as was done with quicksort.
（將集合S-{v}分割成S1和S2，就像我們在快速排序中所作的那樣）

    4. If k <= |S1|, then the kth smallest element must be in S1. In this case, return quickselect (S1, k). If k = 1 + |S1|, then the pivot is the kth smallest element and we can return it as the answer. Otherwise, the kth smallest element lies in S2, and it is the (k - |S1| - 1)st smallest element in S2. We make a recursive call and return quickselect (S2, k - |S1| - 1).
（如果k<=|S1|，那么第k個最小元素必然在S1中。在這種情況下，返回quickselect（S1,k）。如果k=1+|S1|，那么樞紐元素就是第k個最小元素，即找到，直接返回它。否則，這第k個最小元素就在S2中，即S2中的第（k-|S1|-1）（多謝王洋提醒修正）個最小元素，我們遞歸調用并返回quickselect（S2，k-|S1|-1））。

    In contrast to quicksort, quickselect makes only one recursive call instead of two. The worst case of quickselect is identical to that of quicksort and is O(n2). Intuitively, this is because quicksort's worst case is when one of S1 and S2 is empty; thus, quickselect（快速選擇） is not really saving a recursive call. The average running time, however, is O(n)（不過，其平均運行時間為O（N）。看到了沒，就是平均復雜度為O（N）這句話）. The analysis is similar to quicksort's and is left as an exercise.

    The implementation of quickselect is even simpler than the abstract description might imply. The code to do this shown in Figure 7.16. When the algorithm terminates, the kth smallest element is in position k. This destroys the original ordering; if this is not desirable, then a copy must be made. 

并給出了代碼示例：

1. 與快速排序相比，快速選擇只做了一次遞歸調用而不是兩次。快速選擇的最壞情況和快速排序的相同，也是O（N^2），最壞情況發生在樞紐元的選取不當，以致S1，或S2中有一個序列為空。
2. 這就好比快速排序的運行時間與劃分是否對稱有關，劃分的好或對稱，那么快速排序可達最佳的運行時間O（n*logn），劃分的不好或不對稱，則會有最壞的運行時間為O（N^2）。而樞紐元的選取則完全決定快速排序的partition過程是否劃分對稱。
3. 快速選擇也是一樣，如果樞紐元的選取不當，則依然會有最壞的運行時間為O（N^2）的情況發生。那么，怎么避免這個最壞情況的發生，或者說就算是最壞情況下，亦能保證快速選擇的運行時間為O（N）列?對了，關鍵，還是看你的樞紐元怎么選取。
4. 像上述程序使用三數中值作為樞紐元的方法可以使得最壞情況發生的概率幾乎可以忽略不計。然而，稍后，在本文第四節末，及本文文末，您將看到：通過一種更好的方法，如“五分化中項的中項”，或“中位數的中位數”等方法選取樞紐元，我們將能徹底保證在最壞情況下依然是線性O（N）的復雜度。

     至于編程之美上所述：從數組中隨機選取一個數X，把數組劃分為Sa和Sb倆部分，那么這個問題就轉到了下文第二節RANDOMIZED-SELECT，以線性期望時間做選擇，無論如何，編程之美上的解法二的復雜度為O（n*logk）都是有待商榷的。至于最壞情況下一種全新的，為O（N）的快速選擇算法，直接跳轉到本文第四節末，或文末部分吧）。

     不過，為了公正起見，把編程之美第141頁上的源碼貼出來，由大家來評判：

     你已經看到，它是隨機選取數組中的任一元素為樞紐的，這就是本文下面的第二節RANDOMIZED-SELECT的問題了，只是要修正的是，此算法的平均時間復雜度為線性期望O（N）的時間。而，稍后在本文的第四節或本文文末，您還將會看到此問題的進一步闡述（SELECT算法，即快速選擇算法），此SELECT算法能保證即使在最壞情況下，依然是線性O（N）的復雜度。

updated：

   1、為了照顧手中沒編程之美這本書的friends，我拍了張照片，現貼于下供參考（提醒：1、書上為尋找最大的k個數，而我們面對的問題是尋找最小的k個數，兩種形式，一個本質（該修改的地方，上文已經全部修改）。2、書中描述與上文思路4并無原理性出入，不過，勿被圖中記的筆記所誤導，因為之前也曾被書中的這個n*logk復雜度所誤導過。ok，相信，看完本文后，你不會再有此疑惑）：

    2、同時，在編程之美原書上此節的解法五的開頭提到，“上面類似快速排序的方法平均時間復雜度是線性的”，我想上面的類似快速排序的方法，應該是指解法（即如上所述的類似快速排序partition過程的方法），但解法二得出的平均時間復雜度卻為O（N*logk），明擺著前后矛盾（參見下圖）。

    3、此文創作后的幾天，已把本人的意見反饋給鄒欣等人，下面是編程之美bop1的改版修訂地址的頁面截圖（本人也在參加其改版修訂的工作），下面的文字是我的記錄（同時，本人聲明，此狂想曲系列文章系我個人獨立創作，與其它的事不相干）：

第二節、Randomized-Select，線性期望時間
   下面是RANDOMIZED-SELECT(A, p, r)完整偽碼（來自算法導論），我給了注釋，或許能給你點啟示。在下結論之前，我還需要很多的時間去思量，以確保結論之完整與正確。

PARTITION(A, p, r)         //partition過程 p為第一個數，r為最后一個數
1  x ← A[r]               //以最后一個元素作為主元
2  i ← p - 1
3  for j ← p to r - 1
4       do if A[j] ≤ x
5             then i ← i + 1
6                  exchange A[i] <-> A[j]
7  exchange A[i + 1] <-> A[r]
8  return i + 1

RANDOMIZED-PARTITION(A, p, r)      //隨機快排的partition過程
1  i ← RANDOM(p, r)                                 //i  隨機取p到r中個一個值
2  exchange A[r] <-> A[i]                         //以隨機的 i作為主元
3  return PARTITION(A, p, r)            //調用上述原來的partition過程

RANDOMIZED-SELECT(A, p, r, i)       //以線性時間做選擇，目的是返回數組A[p..r]中的第i 小的元素
1  if p = r          //p=r，序列中只有一個元素 
2      then return A[p]
3  q ← RANDOMIZED-PARTITION(A, p, r)   //隨機選取的元素q作為主元 
4  k ← q - p + 1                     //k表示子數組 A[p…q]內的元素個數，處于劃分低區的元素個數加上一個主元元素
5  if i == k                        //檢查要查找的i 等于子數組中A[p....q]中的元素個數k
6      then return A[q]        //則直接返回A[q] 
7  else if i < k       
8      then return RANDOMIZED-SELECT(A, p, q - 1, i)   
          //得到的k 大于要查找的i 的大小，則遞歸到低區間A[p，q-1]中去查找
9  else return RANDOMIZED-SELECT(A, q + 1, r, i - k)
          //得到的k 小于要查找的i 的大小，則遞歸到高區間A[q+1，r]中去查找。  

    寫此文的目的，在于起一個拋磚引玉的作用。希望，能引起你的重視及好的思路，直到有個徹底明白的結果。

     updated：算法導論原英文版有關于RANDOMIZED-SELECT(A, p, r)為O（n）的證明。為了一個徹底明白的闡述，我現將其原文的證明自個再翻譯加工后，闡述如下：

此RANDOMIZED-SELECT最壞情況下時間復雜度為Θ(n²),即使是要選擇最小元素也是如此，因為在劃分時可能極不走運，總是按余下元素中的最大元素進行劃分，而劃分操作需要O（n）的時間。

然而此算法的平均情況性能極好，因為它是隨機化的，故沒有哪一種特別的輸入會導致其最壞情況的發生。

算法導論上，針對此RANDOMIZED-SELECT算法平均時間復雜度為O（n）的證明，引用如下，或許，能給你我多點的啟示（本來想直接引用第二版中文版的翻譯文字，但在中英文對照閱讀的情況下，發現第二版中文版的翻譯實在不怎么樣，所以，得自己一個一個字的敲，最終敲完修正如下），分4步證明：

1、當RANDOMIZED-SELECT作用于一個含有n個元素的輸入數組A[p ..r]上時，所需時間是一個隨機變量，記為T(n),我們可以這樣得到線性期望值E [T(n)]的下界：程序RANDOMIZED-PARTITION會以等同的可能性返回數組中任何一個元素為主元，因此，對于每一個k，（1 ≤k ≤n）,子數組A[p ..q]有k個元素，它們全部小于或等于主元元素的概率為1/n.對k = 1, 2,...,n,我們定指示器X_k，為：

X_k = I{子數組A[p ..q]恰有k個元素} ,

我們假定元素的值不同，因此有

          E[Xk]=1/n

當調用RANDOMIZED-SELECT并且選擇A[q]作為主元元素的時候,我們事先不知道是否會立即找到我們所想要的第i小的元素，因為，我們很有可能需要在子數組A[p ..q - 1], 或A[q + 1 ..r]上遞歸繼續進行尋找.具體在哪一個子數組上遞歸尋找，視第i小的元素與A[q]的相對位置而定.

2、假設T(n)是單調遞增的，我們可以將遞歸所需時間的界限限定在輸入數組時可能輸入的所需遞歸調用的最大時間（此句話，原中文版的翻譯也是有問題的）.換言之,我們斷定,為得到一個上界，我們假定第i小的元素總是在劃分的較大的一邊，對一個給定的RANDOMIZED-SELECT,指示器Xk剛好在一個k值上取1，在其它的k值時，都是取0.當Xk =1時，可能要遞歸處理的倆個子數組的大小分別為k-1，和n-k，因此可得到遞歸式為

         

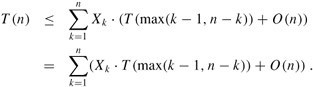
取期望值為：
        

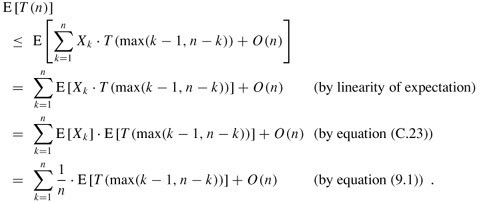
為了能應用等式(C.23),我們依賴于X_k和T(max(k - 1,n - k))是獨立的隨機變量（這個可以證明，證明此處略）。

3、下面，我們來考慮下表達式max(k - 1,n -k)的結果.我們有：

         

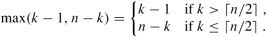
如果n是偶數，從T(⌉)到T(n - 1)每個項在總和中剛好出現倆次，T(⌋)出現一次。因此，有

         

我們可以用替換法來解上面的遞歸式。假設對滿足這個遞歸式初始條件的某個常數c，有T(n) ≤cn。我們假設對于小于某個常數c（稍后再來說明如何選取這個常數）的n，有T(n) =O(1)。 同時，還要選擇一個常數a，使得對于所有的n>0，由上式中O(n)項(用來描述這個算法的運行時間中非遞歸的部分)所描述的函數，可由an從上方限界得到（這里，原中文版的翻譯的確是有點含糊）。利用這個歸納假設，可以得到：

（此段原中文版翻譯有點問題，上述文字已經修正過來，對應的此段原英文為：We solve the recurrence by substitution. Assume thatT(n)≤cn for some constant c that satisfies the initial conditions of the recurrence. We assume thatT(n) =O(1) forn less than some constant; we shall pick this constant later. We also pick a constanta such that the function described by theO(n) term above (which describes the non-recursive component of the running time of the algorithm) is bounded from above byan for alln> 0. Using this inductive hypothesis, we have）

        

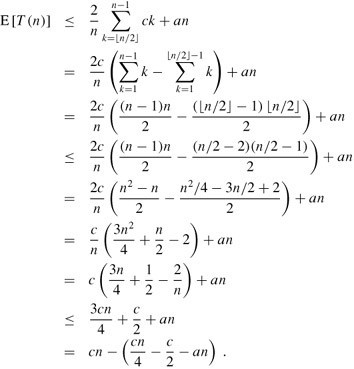
4、為了完成證明，還需要證明對足夠大的n，上面最后一個表達式最大為cn，即要證明：cn/4 -c/2 -an ≥ 0.如果在倆邊加上c/2，并且提取因子n，就可以得到n(c/4 -a) ≥c/2.只要我們選擇的常數c能滿足c/4 -a > 0, i.e.,即c > 4a,我們就可以將倆邊同時除以c/4 -a, 最終得到：

                 

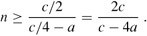
綜上，如果假設對n < 2c/(c -4a),有T(n) =O(1)，我們就能得到E[T(n)] =O(n)。所以，最終我們可以得出這樣的結論，并確認無疑：在平均情況下，任何順序統計量（特別是中位數）都可以在線性時間內得到。

      結論： 如你所見，RANDOMIZED-SELECT有線性期望時間O（N）的復雜度，但此RANDOMIZED-SELECT算法在最壞情況下有O（N^2）的復雜度。所以，我們得找出一種在最壞情況下也為線性時間的算法。稍后，在本文的第四節末，及本文文末部分，你將看到一種在最壞情況下是線性時間O（N）的復雜度的快速選擇SELECT算法。

第三節、各執己見，百家爭鳴

updated ：本文昨晚發布后，現在朋友們之間，主要有以下幾種觀點（在徹底弄清之前，最好不要下結論）：

1. luuillu：我不認為隨機快排比直接快排的時間復雜度小。使用快排處理數據前，我們是不知道數據的排列規律的，因此一般情況下，被處理的數據本來就是一組隨機數據，對于隨機數據再多進行一次隨機化處理，數據仍然保持隨機性，對排序沒有更好的效果。   對一組數據采用隨選主元的方法，在極端的情況下，也可能出現每次選出的主元恰好是從大到小排列的，此時時間復雜度為O（n^2）.當然這個概率極低。隨機選主元的好處在于，由于在現實中常常需要把一些數據保存為有序數據，因此，快速排序碰到有序數據的概率就會高一些，使用隨機快排可以提高對這些數據的處理效率。這個概率雖然高一些，但仍屬于特殊情況，不影響一般情況的時間復雜度。我覺得樓主上面提到的的思路4和思路5的時間復雜度是一樣的。
2. 571樓 得分：0 Sorehead 回復于：2011-03-09 16:29:58
   關于第五題：
   Sorehead： 這兩天我總結了一下，有以下方法可以實現：
         1、第一次遍歷取出最小的元素，第二次遍歷取出第二小的元素，依次直到第k次遍歷取出第k小的元素。這種方法最簡單，時間復雜度是O(k*n)。看上去效率很差，但當k很小的時候可能是最快的。
         2、對這n個元素進行排序，然后取出前k個數據即可，可以采用比較普遍的堆排序或者快速排序，時間復雜度是O(n*logn)。這種方法有著很大的弊端，題目并沒有要求這最小的k個數是排好序的，更沒有要求對其它數據進行排序，對這些數據進行排序某種程度上來講完全是一種浪費。而且當k=1時，時間復雜度依然是O(n*logn)。
         3、可以把快速排序改進一下，應該和樓主的kth_elem一樣，這樣的好處是不用對所有數據都進行排序。平均時間復雜度應該是O(n*logk)。（在本文最后一節，你或將看到，復雜度可能應該為O（n））
         4、使用我開始講到的平衡二叉樹或紅黑樹，樹只用來保存k個數據即可，這樣遍歷所有數據只需要一次。時間復雜度為O(n*logk)。后來我發現這個思路其實可以再改進，使用堆排序中的堆，堆中元素數量為k，這樣堆中最大元素就是頭節點，遍歷所有數據時比較次數更少，當然時間復雜度并沒有變化。
         5、使用計數排序的方法，創建一個數組，以元素值為該數組下標，數組的值為該元素在數組中出現的次數。這樣遍歷一次就可以得到這個數組，然后查詢這個數組就可以得到答案了。時間復雜度為O(n)。如果元素值沒有重復的，還可以使用位圖方式。這種方式有一定局限性，元素必須是正整數，并且取值范圍不能太大，否則就造成極大的空間浪費，同時時間復雜度也未必就是O(n)了。當然可以再次改進，使用一種比較合適的哈希算法來代替元素值直接作為數組下標。
3. litaoye：按照算法導論上所說的，最壞情況下線性時間找第k大的數。證明一下：把數組中的元素，5個分為1組排序，排序需要進行7次比較(2^7 > 5!)，這樣需要1.4 * n次比較，可以完成所有組的排序。取所有組的中位數，形成一個新的數組，有n/5個元素，5個分為1組排序，重復上面的操作，直到只剩下小于5個元素，找出中位數。根據等比數列求和公式，求出整個過程的比較次數：7/5 + 7/25 + 7/125 +...... = 7/4，用7/4 * n次比較可以找出中位數的中位數M。能夠證明，整個數組中>=M的數超過3*n / 10 - 6，<=M的數超過3*n / 10 - 6。以M為基準，執行上面的PARTITION，每次至少可以淘汰3*n / 10 - 6，約等于3/10 * n個數，也就是說是用(7/4 + 1) * n次比較之后，最壞情況下可以讓數據量變為原來的7/10，同樣根據等比數列求和公式，可以算出最壞情況下找出第k大的數需要的比較次數，1 + 7/10 + 49/100 + .... = 10/3, 10/3 * 11/4 * n = 110/12 * n，也就是說整個過程是O(n)的，盡管隱含的常數比較大 。

 總結：

      關于RANDOMIZED-SELECT(A, q + 1, r, i - k)，期望運行時間為O（n）已經沒有疑問了，更嚴格的論證在上面的第二節也已經給出來了。

         ok，現在，咱們剩下的問題是，除了此RANDOMIZED-SELECT(A, q + 1, r, i - k)方法（實用價值并不大）和計數排序，都可以做到O（n）之外，還有類似快速排序的partition過程，是否也能做到O（n）?

第四節、類似partition過程，最壞亦能做到O（n）?

   我想，經過上面的各路好漢的思路轟炸，您的頭腦和思維肯定有所混亂了。ok，下面，我盡量以通俗易懂的方式來繼續闡述咱們的問題。上面第三節的總結提出了一個問題，即類似快速排序的partition過程，是否也能做到O（n）?

    我們說對n個數進行排序，快速排序的平均時間復雜度為O（n*logn），這個n*logn的時間復雜度是如何得來的列?

   經過之前我的有關快速排序的三篇文章，相信您已經明了了以下過程：快速排序每次選取一個主元X，依據這個主元X，每次把整個序列劃分為A，B倆個部分，且有Ax<X<Bx。

   假如我們每次劃分總是產生9:1 的劃分，那么，快速排序運行時間的遞歸式為：T（n）=T（9n/10）+T（n/10）+cn。形成的遞歸樹，（注：最后同樣能推出T（n）=n*logn，即如下圖中，每一層的代價為cn，共有logn層（深度），所以，最后的時間復雜度為O（n）*logn）如下：

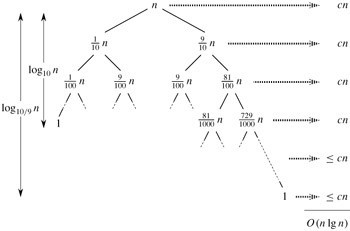
    而我們知道，如果我們每次劃分都是平衡的，即每次都劃分為均等的兩部分元素（對應上圖，第一層1/2,1/2，，第二層1/4，1/4.....），那么，此時快速排序的運行時間的遞歸式為：

    T (n) ≤ 2T (n/2) + Θ(n) ,同樣，可推導出：T (n) = O(n lg n).

    這就是快速排序的平均時間復雜度的由來。

    那么，咱們要面對的問題是什么，要尋找n個數的序列中前k個元素。如何找列?假設咱們首先第一次對n個數運用快速排序的partition過程劃分，主元為Xm，此刻找到的主元元素Xm肯定為序列中第m小的元素，此后，分為三種情況：
    1、如果m=k，即返回的主元即為我們要找的第k小的元素，那么直接返回主元Xm即可，然后直接輸出Xm前面的m-1個元素，這m個元素，即為所求的前k個最小的元素。
    2、如果m>k，那么接下來要到低區間A[0....m-1]中尋找，丟掉高區間；
    3、如果m<k，那么接下來要到高區間A[m+1...n-1]中尋找，丟掉低區間。

    當m一直>k的時候，好說，區間總是被不斷的均分為倆個區間（理想情況），那么最后的時間復雜度如luuillu所說，T(n)=n + T(n/2) = n + n/2 + n/4 + n/8 + ...+1 . 式中一共logn項。可得出：T（n）為O（n）。
    但當m<k的時候，上述情況，就不好說了。正如luuillu所述：當m<k，那么接下來要到高區間A[m+1...n-1]中尋找,新區間的長度為n-m-1, 需要尋找 k-m個數。此時可令：k=k-m, m=n-m-1, 遞歸調用原算法處理，本次執行次數為 m,當m減到1算法停止（當m<k 時 ,k=m-k.這個判斷過程實際上相當于對m取模運算，即：k=k%m;）。
    最終在高區間找到的k-m個數，加上在低區間的k個數，即可找到最小的k個數，是否也能得出T（n）=O（n），則還有待驗證（本文已經全面更新，所有的論證，都已經給出，確認無誤的是：類似快速排序的partition過程，明確的可以做到O（N））。 

 Ok，如果在評論里回復，有諸多不便，歡迎到此帖子上回復：微軟100題維護地址，我會隨時追蹤這個帖子。謝謝。

  updated：

   近日，再次在Mark Allen Weiss的數據結構與算法分析一書上，第10章，第10.2.3節看到了關于此分治算法的應用，平均時間復雜度為O（N）的闡述與證明，可能本文之前的敘述將因此而改寫（July、updated，2011.05.05）：

   The selection problem requires us to find the kth smallest element in a list S of n elements（要求我們找出含N個元素的表S中的第k個最小的元素）. Of particular interest is the special case of finding the median. This occurs when k = |-n/2-|（向上取整）.（我們對找出中間元素的特殊情況有著特別的興趣，這種情況發生在k=|-n/2-|的時候）

    In Chapters 1, 6, 7 we have seen several solutions to the selection problem. The solution in Chapter 7 uses a variation of quicksort and runs in O(n) average time（第7章中的解法，即本文上面第1節所述的思路4，用到快速排序的變體并以平均時間O（N）運行）. Indeed, it is described in Hoare's original paper on quicksort.

    Although this algorithm runs in linear average time, it has a worst case of O (n2)（但它有一個O（N^2）的最快情況）. Selection can easily be solved in O(n log n) worst-case time by sorting the elements, but for a long time it was unknown whether or not selection could be accomplished in O(n) worst-case time. The quickselect algorithm outlined in Section 7.7.6 is quite efficient in practice, so this was mostly a question of theoretical interest.

    Recall that the basic algorithm is a simple recursive strategy. Assuming that n is larger than the cutoff point where elements are simply sorted, an element v, known as the pivot, is chosen. The remaining elements are placed into two sets, S1 and S2. S1 contains elements that are guaranteed to be no larger than v, and S2 contains elements that are no smaller than v. Finally, if k <= |S1|, then the kth smallest element in S can be found by recursively computing the kth smallest element in S1. If k = |S1| + 1, then the pivot is the kth smallest element. Otherwise, the kth smallest element in S is the (k - |S1| -1 )st smallest element in S2. The main difference between this algorithm and quicksort is that there is only one subproblem to solve instead of two（這個快速選擇算法與快速排序之間的主要區別在于，這里求解的只有一個子問題，而不是兩個子問題）。

定理10.9
The running time of quickselect using median-of-median-of-five partitioning is O(n)。

    The basic idea is still useful. Indeed, we will see that we can use it to improve the expected number of comparisons that quickselect makes. To get a good worst case, however, the key idea is to use one more level of indirection. Instead of finding the median from a sample of random elements, we will find the median from a sample of medians.

The basic pivot selection algorithm is as follows:
    1. Arrange the n elements into |_n/5_| groups of 5 elements, ignoring the (at most four) extra elements.
    2. Find the median of each group. This gives a list M of |_n/5_| medians.
    3. Find the median of M. Return this as the pivot, v.

 We will use the term median-of-median-of-five partitioning to describe the quickselect algorithm that uses the pivot selection rule given above. （我們將用術語“五分化中項的中項”來描述使用上面給出的樞紐元選擇法的快速選擇算法）。We will now show that median-of-median-of-five partitioning guarantees that each recursive subproblem is at most roughly 70 percent as large as the original（現在我們要證明，“五分化中項的中項”，得保證每個遞歸子問題的大小最多為原問題的大約70%）. We will also show that the pivot can be computed quickly enough to guarantee an O (n) running time for the entire selection algorithm（我們還要證明，對于整個選擇算法，樞紐元可以足夠快的算出，以確保O（N）的運行時間。看到了沒，這再次佐證了我們的類似快速排序的partition過程的分治方法為O（N）的觀點）。
   ..........
    證明從略，更多，請參考Mark Allen Weiss的數據結構與算法分析--c語言描述一書上，第10章，第10.2.3節。

updated again：

        為了給讀者一個徹徹底底、明明白白的論證，我還是決定把書上面的整個論證過程全程貼上來，下面，接著上面的內容，然后直接從其中文譯本上截兩張圖來說明好了（更清晰明了）：

 

關于上圖提到的定理10.8，如下圖所示，至于證明，留給讀者練習（可參考本文第二節關于RANDOMIZED-SELECT為線性時間的證明）：

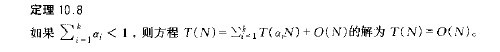
 ok，第四節，有關此問題的更多論述，請參見下面的本文文末updated again部分。

第五節、堆結構實現，處理海量數據

    文章，可不能這么完了，咱們還得實現一種靠譜的方案，從整個文章來看，處理這個尋找最小的k個數，最好的方案是第一節中所提到的思路3：當然，更好的辦法是維護k個元素的最大堆，原理與上述第2個方案一致，即用容量為k的最大堆存儲最小的k個數，此時，k1<k2<...<kmax（kmax設為大頂堆中最大元素）。遍歷一次數列，n，每次遍歷一個元素x，與堆頂元素比較，x<kmax，更新堆（用時logk），否則不更新堆。這樣下來，總費時O（n*logk）。

    為什么?道理很簡單，如果要處理的序列n比較小時，思路2（選擇排序）的n*k的復雜度還能說得過去，但當n很大的時候列?同時，別忘了，如果選擇思路1（快速排序），還得在數組中存儲n個數。當面對海量數據處理的時候列?n還能全部存放于電腦內存中么?（或許可以，或許很難）。

    ok，相信你已經明白了我的意思，下面，給出借助堆（思路3）這個數據結構，來尋找最小的k個數的完整代碼，如下：

    咱們用比較大量的數據文件測試一下，如這個數據文件：

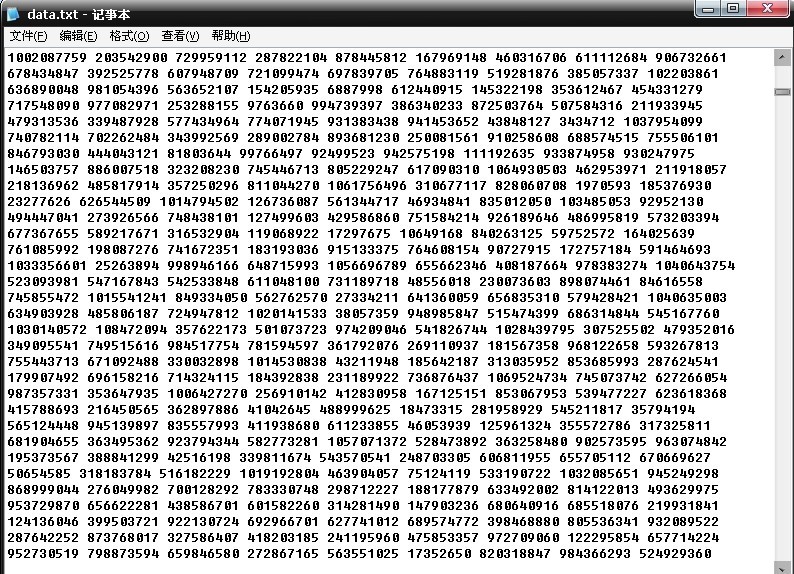
    輸入k=4，即要從這大量的數據中尋找最小的k個數，可得到運行結果，如下圖所示：

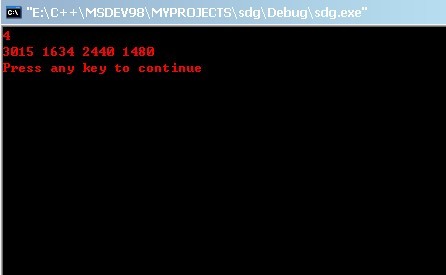
至于，這4個數，到底是不是上面大量數據中最小的4個數，這個，咱們就無從驗證了，非人力之所能及也。畢。

第六節、stl之_nth_element ，逐步實現

    以下代碼摘自stl中_nth_element的實現，且逐步追蹤了各項操作，其完整代碼如下：

第七節、再探Selection_algorithm，類似partition方法O（n）再次求證

網友反饋：
    stupidcat：用類似快排的partition的方法，只求2邊中的一邊，在O(N)時間得到第k大的元素v； 
弄完之后，vector<int> &data的前k個元素，就是最小的k個元素了。 
時間復雜度是O(N)，應該是最優的算法了。并給出了代碼示例：

    這個算法，其實就是在本人這篇文章：當今世界最受人們重視的十大經典算法里提到的：第三名：BFPRT 算法：

A worst-case linear algorithm for the general case of selecting the kth largest element was published by Blum,
Floyd, Pratt, Rivest and Tarjan in their 1973 paper "Time bounds for selection", 
sometimes called BFPRT after the last names of the authors. 
It is based on the quickselect algorithm and is also known as the median-of-medians algorithm.

    同時據維基百科上指出，若能選取一個好的pivot，則此算法能達到O（n）的最佳時間復雜度。

The median-calculating recursive call does not exceed worst-case linear behavior 
because the list of medians is 20% of the size of the list, 
while the other recursive call recurs on at most 70% of the list, making the running time
 
T(n) ≤ T(n/5) + T(7n/10) + O(n)

The O(n) is for the partitioning work (we visited each element a constant number of times，
in order to form them into O(n) groups and take each median in O(1) time). 
From this, one can then show that T(n) ≤ c*n*(1 + (9/10) + (9/10)2 + ...) = O(n).

    當然，上面也提到了用堆這個數據結構，掃描一遍數組序列，建k個元素的堆O（k）的同時，調整堆（logk），然后再遍歷剩下的n-k個元素，根據其與堆頂元素的大小比較，決定是否更新堆，更新一次logk，所以，最終的時間復雜度為O（k*logk+(n-k)*logk）=O（n*logk）。

Another simple method is to add each element of the list into an ordered set data structure,
such as a heap or self-balancing binary search tree, with at most k elements. 
Whenever the data structure has more than k elements, we remove the largest element,
which can be done in O(log k) time. Each insertion operation also takes O(log k) time,
resulting in O(nlog k) time overall.

    而如果上述類似快速排序的partition過程的BFPRT 算法成立的話，則將最大限度的優化了此尋找第k個最小元素的算法復雜度（經過第1節末+第二節+第4節末的updated，以及本節的論證，現最終確定，運用類似快速排序的partition算法尋找最小的k個元素能做到O（N）的復雜度，并確認無疑。July、updated，2011.05.05.凌晨）。

updated again：

   為了再次佐證上述論證之不可懷疑的準確性，我再原文引用下第九章第9.3節全部內容（最壞情況線性時間的選擇），如下（我酌情對之參考原中文版做了翻譯，下文中括號內的中文解釋，為我個人添加）：

9.3 Selection in worst-case linear time（最壞情況下線性時間的選擇算法）

    We now examine a selection algorithm whose running time isO(n) in the worst case（現在來看，一個最壞情況運行時間為O（N）的選擇算法SELECT）. Like RANDOMIZED-SELECT, the algorithm SELECT finds the desired element by recursively partitioning the input array. The idea behind the algorithm, however, is toguarantee a good split when the array is partitioned. SELECT uses the deterministic partitioning algorithm PARTITION from quicksort (seeSection 7.1), modified to take the element to partition around as an input parameter（像RANDOMIZED-SELECT一樣，SELECTT通過輸入數組的遞歸劃分來找出所求元素，但是，該算法的基本思想是要保證對數組的劃分是個好的劃分。SECLECT采用了取自快速排序的確定性劃分算法partition，并做了修改，把劃分主元元素作為其參數）.

    The SELECT algorithm determines theith smallest of an input array ofn > 1 elements by executing the following steps. (Ifn = 1, then SELECT merely returns its only input value as theith smallest.)（算法SELECT通過執行下列步驟來確定一個有n>1個元素的輸入數組中的第i小的元素。（如果n=1，則SELECT返回它的唯一輸入數值作為第i個最小值。））

1. Divide then elements of the input array into⌋ groups of 5 elements each and at most one group made up of the remainingn mod 5 elements.
2. Find the median of each of the⌉ groups by first insertion sorting the elements of each group (of which there are at most 5) and then picking the median from the sorted list of group elements.
3. Use SELECT recursively to find the medianx of the⌉ medians found in step 2. (If there are an even number of medians, then by our convention,x is the lower median.)
4. Partition the input array around the median-of-mediansx using the modified version of PARTITION. Letk be one more than the number of elements on the low side of the partition, so thatx is thekth smallest element and there aren-k elements on the high side of the partition.（利用修改過的partition過程，按中位數的中位數x對輸入數組進行劃分，讓k比劃低去的元素數目多1，所以，x是第k小的元素，并且有n-k個元素在劃分的高區）
5. Ifi =k, then returnx. Otherwise, use SELECT recursively to find theith smallest element on the low side ifi <k, or the (i -k)th smallest element on the high side ifi >k.（如果要找的第i小的元素等于程序返回的k，即i=k，則返回x。否則，如果i<k，則在低區遞歸調用SELECT以找出第i小的元素，如果i>k，則在高區間找第（i-k）個最小元素）

（以上五個步驟，即本文上面的第四節末中所提到的所謂“五分化中項的中項”的方法。）

 

    To analyze the running time of SELECT, we first determine a lower bound on the number of elements that are greater than the partitioning element x. （為了分析SELECT的運行時間，先來確定大于劃分主元元素x的的元素數的一個下界）Figure 9.1 is helpful in visualizing this bookkeeping. At least half of the medians found in step 2 are greater than^[1] the median-of-medians x. Thus, at least half of the ⌉ groupscontribute 3 elements that are greater than x, except for the one group that has fewer than 5 elements if 5 does not dividen exactly, and the one group containingx itself. Discounting these two groups, it follows that the number of elements greater thanx is at least：

   

 

   
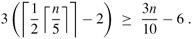
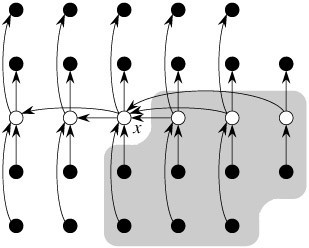
    （Figure 9.1: 對上圖的解釋或稱對SELECT算法的分析：n個元素由小圓圈來表示，并且每一個組占一縱列。組的中位數用白色表示，而各中位數的中位數x也被標出。（當尋找偶數數目元素的中位數時，使用下中位數）。箭頭從比較大的元素指向較小的元素，從中可以看出，在x的右邊，每一個包含5個元素的組中都有3個元素大于x，在x的左邊，每一個包含5個元素的組中有3個元素小于x。大于x的元素以陰影背景表示。 ）

    Similarly, the number of elements that are less thanx is at least 3n/10 - 6. Thus, in the worst case, SELECT is called recursively on at most 7n/10 + 6 elements in step 5.

    We can now develop a recurrence for the worst-case running timeT(n) of the algorithm SELECT. Steps 1, 2, and 4 take O(n) time. (Step 2 consists ofO(n) calls of insertion sort on sets of sizeO(1).) Step 3 takes timeT(⌉), and step 5 takes time at mostT(7n/10+ 6), assuming thatT is monotonically increasing. We make the assumption, which seems unmotivated at first, that any input of 140 or fewer elements requiresO(1) time; the origin of the magic constant 140 will be clear shortly. We can therefore obtain the recurrence：

         

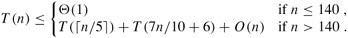
    We show that the running time is linear by substitution. More specifically, we will show thatT(n) ≤cn for some suitably large constant c and alln > 0. We begin by assuming thatT(n) ≤cn for some suitably large constantc and alln ≤ 140; this assumption holds ifc is large enough. We also pick a constanta such that the function described by theO(n) term above (which describes the non-recursive component of the running time of the algorithm) is bounded above byan for alln > 0. Substituting this inductive hypothesis into the right-hand side of the recurrence yields

 

T(n)	≤	c⌉ +c(7n/10 + 6) +an
	≤	cn/5 +c + 7cn/10 + 6c +an
	=	9cn/10 + 7c +an
	=	cn + (-cn/10 + 7c +an) ,

 

 

 

 

 

 

 

 

 

 

which is at mostcn if

              

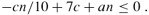
Inequality (9.2) is equivalent to the inequalityc ≥ 10a(n/(n - 70)) when n > 70. Because we assume thatn ≥ 140, we have n/(n - 70) ≤ 2, and so choosing c ≥ 20a will satisfyinequality (9.2). (Note that there is nothing special about the constant 140; we could replace it by any integer strictly greater than 70 and then choosec accordingly.) The worst-case running time of SELECT is therefore linear（因此，此SELECT的最壞情況的運行時間是線性的）.

 

    As in a comparison sort (seeSection 8.1), SELECT and RANDOMIZED-SELECT determine information about the relative order of elements only by comparing elements. Recall fromChapter 8 that sorting requiresΩ(n lgn) time in the comparison model, even on average (see Problem 8-1). The linear-time sorting algorithms in Chapter 8 make assumptions about the input. In contrast, the linear-time selection algorithms in this chapter do not require any assumptions about the input. They are not subject to the Ω(nlgn) lower bound because they manage to solve the selection problem without sorting.

（與比較排序（算法導論8.1節）中的一樣，SELECT和RANDOMIZED-SELECT僅通過元素間的比較來確定它們之間的相對次序。在算法導論第8章中，我們知道在比較模型中，即使在平均情況下，排序仍然要O（n*logn）的時間。第8章得線性時間排序算法在輸入上做了假設。相反地，本節提到的此類似partition過程的SELECT算法不需要關于輸入的任何假設，它們不受下界O（n*logn）的約束，因為它們沒有使用排序就解決了選擇問題（看到了沒，道出了此算法的本質阿））

    Thus, the running time is linear because these algorithms do not sort; the linear-time behavior is not a result of assumptions about the input, as was the case for the sorting algorithms inChapter 8. Sorting requiresΩ(n lgn) time in the comparison model, even on average (see Problem 8-1), and thus the method of sorting and indexing presented in the introduction to this chapter is asymptotically inefficient.（所以，本節中的選擇算法之所以具有線性運行時間，是因為這些算法沒有進行排序；線性時間的結論并不需要在輸入上所任何假設，即可得到。.....）  

ok，綜述全文，根據選取不同的元素作為主元（或樞紐）的情況，可簡單總結如下：
1、RANDOMIZED-SELECT，以序列中隨機選取一個元素作為主元，可達到線性期望時間O（N）的復雜度。
    這個在本文第一節有關編程之美第2.5節關于尋找最大的k個元素（但其n*logk的復雜度是嚴重錯誤的，待勘誤,應以算法導論上的為準，隨機選取主元，可達線性期望時間的復雜度），及本文第二節中涉及到的算法導論上第九章第9.2節中（以線性期望時間做選擇），都是以隨機選取數組中任一元素作為樞紐元的。

2、SELECT，快速選擇算法，以序列中“五分化中項的中項”，或“中位數的中位數”作為主元（樞紐元），則不容置疑的可保證在最壞情況下亦為O（N）的復雜度。
    這個在本文第四節末，及本文第七節，本文文末中都有所闡述，具體涉及到了算法導論一書中第九章第9.3節的最快情況線性時間的選擇，及Mark Allen Weiss所著的數據結構與算法分析--c語言描述一書的第10章第10.2.3節（選擇問題）中，都有所闡述。

       本文結論：至此，可以毫無保留的確定此問題之結論：運用類似快速排序的partition的快速選擇SELECT算法尋找最小的k個元素能做到O（N）的復雜度。RANDOMIZED-SELECT可能會有O（N^2）的最壞的時間復雜度，但上面的SELECT算法，采用如上所述的“中位數的中位數”的取元方法，則可保證此快速選擇算法在最壞情況下是線性時間O（N）的復雜度。

       最終驗證：

        1、我想，我想，是的，僅僅是我猜想，你可能會有這樣的疑問：經過上文大量嚴謹的論證之后，利用SELECT算法，以序列中“五分化中項的中項”，或“中位數的中位數”作為主元（樞紐元），的的確確在最壞情況下O（N）的時間復雜度內找到第k小的元素，但是，但是，咱們的要面對的問題是什么?咱們是要找最小的k個數阿！不是找第k小的元素，而是找最小的k個數（即不是要你找1個數，而是要你找k個數）?哈哈，問題提的非常之好阿。

        2、事實上，在最壞情況下，能在O（N）的時間復雜度內找到第k小的元素，那么，亦能保證最壞情況下在O（N）的時間復雜度內找到前最小的k個數，咱們得找到一個理論依據，即一個證明（我想，等你看到找到前k個數的時間復雜度與找第k小的元素，最壞情況下，同樣是O（N）的時間復雜度后，你便會100%的相信本文的結論了，然后可以通告全世界，你找到了這個世界上最靠譜的中文算法blog，ok，這是后話）。

        算法導論第9章第9.3節練習里，有2個題目，與我們將要做的證明是一個道理，請看：

Exercises 9.3-4: ⋆ 
Suppose that an algorithm uses only comparisons to find the ith smallest element in a set of n elements. Show that it can also find the i - 1 smaller elements and the n - i larger elements without performing any additional comparisons.（假設對一個含有n個元素的集合，某算法只需比較來確定第i小的元素。證明：無需另外的比較操作，它也能找到比i 小的i-1個元素和比i大的n-i個元素）。

Exercises 9.3-7 
Describe an O(n)-time algorithm that, given a set S of n distinct numbers and a positive integer k ≤ n, determines the k numbers in S that are closest to the median of S.（給出一個O（N）時間的算法，在給定一個有n個不同數字的集合S以及一個正整數K<=n后，它能確定出S中最接近其中位數的k個數。）

      怎么樣，能證明么?既然通過本文，咱們已經證明了上述的SELECT算法在最壞情況下O（N）的時間內找到第k小的元素，那么距離咱們確切的問題：尋找最小的k個數的證明，只差一步之遙了。

      給點提示：

      1、找到了第K小的數Xk 為O(n)，再遍歷一次數組，找出所有比k小的元素O（N）（比較Xk與數組中各數的大小，凡是比Xk小的元素，都是我們要找的元素），最終時間復雜度即為： O（N）（找到第k小的元素） + 遍歷整個數組O（N）=O（N）。這個結論非常之簡單，也無需證明（但是，正如上面的算法導論練習題9.3-7所述，能否在找到第k小的元素后，能否不需要再比較元素列?）。

      2、我們的問題是，找到 第k小的元素后Xk，是否Xk之前的元素就是我們 要找的最小 的k個數，即，Xk前面的數，是否都<=Xk?因為 那樣的話，復雜度則 變為：O（N）+O（K）（遍歷找到的第k小元素 前面的k個元素）=O（N+K）=O（N），最壞情況下，亦是線性時間。

     終極結論：證明只有一句話：因為本文我們所有的討論都是基于快速排序的partition方法，而這個方法，每次劃分之后，都保證了 樞紐元Xk的前邊元素統統小于Xk，后邊元素統統大于Xk（當然，如果你是屬于那種打破沙鍋問到底的人，你可能還想要我證明partition過程中樞紐元素為何能把整個序列分成左小右大兩個部分。但這個不屬于本文討論范疇。讀者可參考算法導論第7章第7.1節關于partition過程中循環不變式的證明）。所以，正如本文第一節思路5所述在0（n）的時間內找到第k小的元素，然后遍歷輸出前面的k個小的元素。如此，再次驗證了咱們之前得到的結論：運用類似快速排序的partition的快速選擇SELECT算法尋找最小的k個元素，在最壞情況下亦能做到O（N）的復雜度。

    5、RANDOMIZED-SELECT，每次都是隨機選取數列中的一個元素作為主元，在0（n）的時間內找到第k小的元素，然后遍歷輸出前面的k個小的元素。 如果能的話，那么總的時間復雜度為線性期望時間：O（n+k）=O（n）（當k比較小時）。

     所以列，所以，恭喜你，你找到了這個世界上最靠譜的中文算法blog。

     updated：

     我假設，你并不認為并贊同上述那句話：你找到了這個世界上最靠譜的中文算法blog。ok，我再給你一個證據：我再次在編程珠璣II上找到了SELECT算法能在平均時間O（N）內找出第k小元素的第三個證據。同時，依據書上所說，由于SELECT算法采取partition過程劃分整個數組元素，所以在找到第k小的元素Xk之后，Xk+Xk前面的k個元素即為所要查找的k個元素（下圖為編程珠璣II第15章第15.2節的截圖，同時各位還可看到，快速排序是遞歸的對倆個子序列進行操作，而選擇算法只對含有K的那一部分重復操作）。

    再多余的話，我不想說了。我知道我的確是一個庸人自擾的P民，即沒有問題的事情卻硬要弄出一堆問題出來，然后再矢志不渝的論證自己的觀點不容置疑之正確性。ok，畢。

備注：

• 快速選擇SELECT算法，雖然復雜度平均是o(n)，但這個系數比較大，與用一個最大堆0(n*logk)不見得就有優勢） 
• 當K很小時，O（N*logK）與O（N）等價，當K很大時，當然也就不能忽略掉了。也就是說，在我們這個具體尋找k個最小的數的問題中，當我們無法確定K 的具體值時（是小是大），咱們便不能簡單的從表面上忽略。也就是說：O（N*logK）就是O（N*logK），非O（N）。

1. 如果n=1024,k=n-1,最差情況下需比較2n次，而nlog(k-1)=10n，所以不相同。實際上，這個算法時間復雜度與k沒有直接關系。且只在第一次劃分的時候用到了K,后面幾次劃分，是根據實際情況確定的，與K無關了。
2. 但k=n/2時也不是nlogk,因為只在第一次劃分的時候用到了K,后面幾次劃分,是根據實際情況確定的,與K無關了。比如a[1001].k=500,第一次把把a劃分成兩部分,b和c ,不妨設b元素個數為400個,c中元素為600個,則下一步應該舍掉a,然后在c中尋找top100,此時k已經變成了100，因此與k無關。

• 所以，咱們在表述快速選擇算法的平均時間復雜度時，還是要寫成O（N）的，斷不可寫成O（N*logK）的。

參考文獻：
1、Mark Allen Weiss的數據結構與算法分析--c語言描述，第7章第7.7.6節，線性期望時間的選擇算法，第10章第10.2.3節，選擇問題
2、算法導論，第九章第9.2節，以線性期望時間做選擇，第九章第9.3節，最快情況線性時間的選擇
3、編程之美第一版，第141頁，第2.5節 尋找最大的k個數（找最大或最小，一個道理）
4、維基百科，http://en.wikipedia.org/wiki/Selection_algorithm。
5、M. Blum, R.W. Floyd, V. Pratt, R. Rivest and R. Tarjan, "Time bounds for selection,"
J. Comput. System Sci. 7 (1973) 448-461. 
6、當今世界最受人們重視的十大經典算法里提到的，BFPRT 算法。
7、編程珠璣II 第15章第15.2節程序。順便大贊此書。July、updated，2011.05.07。

    預告： 程序員面試題狂想曲、第四章（更多有關海量數據處理，及Top K 算法問題（此問題已作為第三章續），第四章，擇日發布。），五月份發布（近期內事情較多，且昨夜因修正此文足足熬到了凌晨4點（但室內并無海棠花），寫一篇文章太耗精力和時間，見諒。有關本人動態，可關注本人微博：http://weibo.com/julyweibo。謝謝。July、updated，2011.05.05）。

ok，有任何問題，歡迎隨時指出。謝謝。完。