]]>
�W�二十七章:(x��)不改变正负数之间相对��序重新排列数组.旉���O(N)�Q�空间O(1)
前言
在这���文章:(x��)�?ji��)月腾讯�Q�创新工场,淘宝�{�公司最新面试十三题�?span style="font-size: 14px;">�W?�?一个未排序整数数组�Q�有正负敎ͼ�重新排列使负数排在正数前面,�q�且要求不改变原来的正负��C��间相寚w���?�Q�自从去�q�九(ji��)月收录了此题至今�Q�一直未曄�����C�o(h��)人满意的�{�案�Q��ؓ(f��)何呢?
因�ؓ(f��)一般达不到题目所要求的:(x��)旉���复杂度O(N),�I�间O(1)�Q�且保证原来正负��C��间的相对位置不变�?/span>本编�E�艺术系列第27章就来阐�q�这个问题,若有��M��漏洞�Q�欢�q�随时不吝指正。谢谢�?/span>
重新排列使负数排在正数前�?/span>
原题是这��L(f��ng)���Q?/span>
一个未排序整数数组�Q�有正负敎ͼ�重新排列使负数排在正数前面,�q�且要求不改变原来的正负��C��间相寚w��序�?br />比如�Q?input: 1,7,-5,9,-12,15 �Q�ans: -5,-12,1,7,9,15 。且要求旉���复杂度O(N),�I�间O(1) �?/span>
OK�Q�下面咱们就来试着一步一步解�q�道题,如下5�U�思�\�Q�从复杂度O(N^2)到O(N*logN)�Q�从不符合题目条件到一步步���近于条�?�Q�:(x��)
- 最���单的�Q�如果不考虑旉���复杂度,最���单的思�\是从头扫描这个数�l�,每碰��C��个正数时�Q�拿�����个数字,�q�把位于�q�个数字后面的所有数字往前挪动一位。挪完之后在数组的末���有一个空位,�q�时把该正数攑օ��q�个�I�Z��。由于碰��C��个正�Q�需要移动O(n)个数字,因此�ȝ��旉���复杂度是O(n�Q?�?/li>
- 既然题目要求的是把负数放在数�l�的前半部分�Q�正数放在数�l�的后半部分�Q�因此所有的负数应该位于正数的前面。也���是说我们在扫描�q�个数组的时候,如果发现有正数出现在负数的前面,我们可以交换他们的顺序,交换之后���q��合要求了�?br />因此我们可以�l�护两个指针�Q�第一个指针初始化为数�l�的�W�一个数字,它只向后�U�d���Q�第二个指针初始化�ؓ(f��)数组的最后一个数字,它只向前�U�d��。在两个指针盔R��之前�Q�第一个指针��L��位于�W�二个指针的前面。如果第一个指针指向的数字是正而第二个指针指向的数字是负数�Q�我们就交换�q�两个数字�?br />但遗憄���是上�q�方法改变了原来正负��C��间的相对��序。所以,�׃��得另寻良�{?span style="font-family: SimSun; line-height: 25px; font-size: 14px;">�?/span>
首先�Q�定义这样一个过�E��ؓ(f��)“����{”�Q?a1,a2,...,am,b1,b2,...,bn) --> (b1,b2,...,bn,a1,a2,...,am)。其�ơ,对于待处理的未排序整数数�l�,从头到尾�q�行扫描�Q�寻�?正正...正负...负负)�Ԍ��每找到这样一个串�Q�则计数器加1�Q�若计数为奇敎ͼ�则对当前串做一�?#8220;����{”�Q�反复扫描,直到再也找不�?正正...正负...负负)丌Ӏ?/p>
此思�\来自朋友胡果果,�I�间复杂度虽为O(1)�Q?/span>但其旉���复杂度O(N*logN)�?/span>更多具体�l�节参看原文�Q?span style="font-size: 14px;">http://qing.weibo.com/1570303725/5d98eeed33000hcb.html。故�Q�不�W�合题目要求�Q����l�寻找�?/span>
- 我们可以�q�样�Q?/span>讄���一个�v始点j, 一个翻转点k,一个终止点L�Q�从右侧��P��起始点在�W�一个出现的负数, ����{点在起始点后�W�一个出现的正数,�l�止点在����{点后出现的第一个负�?或结�?�?/span>
如果无翻转点, 则不操作�Q�如果有����{�? 则待�l�止点出现后, 做翻�? 即ab => ba �q�样的操作。翻转后, 负数串一定在左侧, 然后从负��C��的右侧开始记录�v始点, �l�箋往下找下一个翻转点�?/p>
例子中的���是(下划�U�代表要交换��序的两个数�?�Q?/p>
1, 7, -5, 9, -12, 15
此思�\2果真解决了么?NO�Q�用下面�q�个例子试一下,我们���p��立马看出了漏�z�:(x��)
�W�一�ơ翻�? 1, 7, -5, -12,9, 15 => 1, -12, -5, 7, 9, 15
�W�二�ơ翻�? -5, -12, 1, 7, 9, 15
1, 7, -5, -6�Q?nbsp;9, -12, 15�Q�此�U�情冉|��能处理)
1 7 -5 -6 -12 9 15
1 -12 -5 -6 7 9 15
-6 -12 -5 1 7 9 15 (此时�Q�正负数之间的相寚w��序已�l�改变,本应该是-5�Q?6�Q?12�Q�而现在是-6 -12 -5) - 看来�q�个问题的确有点�ȝ���Q�不�q�我们最�l�貌��D��是找��C��另外一�U�解军_��法,正如朋友���越���所说的�Q�从后往前扫描,遇到负数�Q�开始记录负数区��_(d��)��然后遇到正数�Q�记录前面的正数区间�Q�然后把整个负数区间与前面的正数区间�q�行交换�Q�交换区间但保序的算法类��|��a,bc->bc,a�Q�的字符串原地翻转算法�?/span>交换完之后要�l�箋向前一直扫描下去,每次���到负数区间在正数区间后面,���q��转区间。下面,���详�l�阐�q�此思�\4�?/span>
思�\5之区间翻�?/span>
10、翻转句子中单词的顺序�?br />题目�Q�输入一个英文句子,����{句子中单词的��序�Q�但单词内字�W�的��序不变。句子中单词以空格符隔开。�ؓ(f��)���单�v见,标点�W�号和普通字母一样处理。例如输�?#8220;I am a student.”�Q�则输出“student. a am I”�?span style="font-family: 'Arial Black';">而此题可以在O(N)的时间复杂度内解�?/span>�Q?/p>
�׃��本题需要翻转句子,我们先颠倒句子中的所有字�W�。这�Ӟ��不但����{了句子中单词的顺序,而且单词内字�W�也被翻转了。我们再颠倒每个单词内的字�W�。由于单词内的字�W�被����{两次�Q�因此顺序仍然和输入时的��序保持一致�?br /> 以上面的输入��Z���Q�翻�?#8220;I am a student.”中所有字�W�得�?#8220;.tneduts a ma I”�Q�再����{每个单词中字�W�的��序得到“students. a am I”�Q�正是符合要求的输出(�~�码实现�Q�可以参看此文:(x��)http://zhedahht.blog.163.com/blog/static/254111742007289205219/)�?br />
对的�Q�上�q�思�\3���是�q�个意思,单词����{便相当于于区间翻转,既如此,�׃��来验证下上述思�\2中那个测试用例,如下�Q?/p>
1, 7, -5, -6�Q?nbsp;9, -12, 15
1 7 -5 -6 -12 9 15
-12 -6 -5 7 1 9 15 (借用单词����{的方法,先逐个数字����{�Q�后正负数整体原地翻�?
-5 -6 -12 1 7 9 15
思�\5再次被质�?/span>
但是�Q�我�q�想再问�Q�问题至此被解决了么?真的被KO了么?NO�Q�咱们来看这样一�U�情况,正如威士忌所��_(d��)��(x��)
看看�q�个数据�Q?-+-+-+-+------+�Q�假如Nminus �{�于 n/2�Q�由于前面都�?-+-+-�Q�区间交换需�?n/2/2 = n/4�ơ,每次交换�?T(2*(Nminus + Nplus)) >= T(n)�Q�n/4 * T(n) = T(n*n/4)=O(n^2)�?/span>
�q�有一�U�更坏的情况�Q�就�?-+-+-+-+------+�q�种数据可能�Q�后面一大堆的负敎ͼ�前面正负交替�?span style="font-size: 14px;">所以,�׃��的美梦再�ơ破灭,路�O漫其修远兮,此题仍然未找��C��个完全解决了的方案�?/span>
]]>
�W�二十五章:(x��)二分查找实现�Q�Jon Bentley�Q?0%�E�序员无法正���实玎ͼ�
作者:(x��)July
出处�Q�结构之法算法之�?/p>
引言
Jon Bentley�Q?0%以上的程序员无法正确无误的写��Z��分查找代码。也许很多�h都早已听说过�q�句话,但我�q�是惛_��用《编�E�珠玑》上的如下几�D�|��字:(x��)
“二分查找可以解决�Q?strong>预排序数�l�的查找�Q�问题:(x��)只要数组中包含T�Q�即要查扄�����|���Q�那么通过不断�~�小包含T的范��_(d��)��最�l�就可以扑ֈ�它。一开始,范围覆盖整个数组。将数组的中间项与T�q�行比较�Q�可以排除一半元素,范围�~�小一半。就�q�样反复比较�Q�反复羃?y��u)��范��_(d��)��最�l�就�?x��)在数组中找到T�Q�或者确定原以�ؓ(f��)T所在的范围实际为空。对于包含N个元素的表,整个查找�q�程大约要经�q�log(2)N�ơ比较�?nbsp;
多数�E�序员都觉得只要理解了上面的描述�Q�写��Z��码就不难了;但事实�ƈ非如此。如果你不认同这一点,最好的办法���是放下书本�Q�自己动手写一写。试试吧�?nbsp;
我在贝尔实验室和IBM的时候都������q�道考题。那些专业的�E�序员有几个���时的时��_(d��)��可以用他们选择的语�a�把上面的描述写出来;写出高��伪代码也可以。考试�l�束后,差不多所有程序员都认�����己写��Z��正确的程序。于是,我们�׃��半个钟头来看他们�~�写的代码经�q�测试用例验证的�l�果。几�ơ课�Q�一癑֤�人的�l�果相差无几�Q?0%的程序员写的�E�序中有bug�Q�我�q�不认�ؓ(f��)没有bug的代码就正确�Q��?nbsp;
我很惊讶�Q�在���_��的时间内�Q�只有大�U?0%的专业程序员可以把这个小�E�序写对。但写不对这个小�E�序的还不止�q�些人:(x��)高�d�U�_��《计���机�E�序设计的艺�?�W?�?排序和查找》第6.2.1节的“历史与参考文�?#8221;部分指出�Q�虽然早�?946�q�就有�h���二分查扄����Ҏ(gu��)��公诸于世�Q�但直到1962�q�才有�h写出没有bug的二分查扄���序�?span style="font-size: 24px;">”——乔恩·本特利,《编�E�珠玑(�W?版)》第35-36���c(di��n)�?/p>
你能正确无误的写��Z��分查找代码么�Q�不妨一试�?/p>
二分查找代码
二分查找的原理想必不用多解释了,不过有一点必���L��醒读者的是,二分查找是针对的排好序的数组。OK�Q�纸上读来终觉浅�Q�觉知此事要�w�行。我先来写一份,下面是我写的一份二分查扄���实现�Q�之前去某一家公叔R��试也曾被叫当场实��C��分查找,不过�l�果可能跟你一��P��当时���未能完整无误写出)�Q�有��M��问题或错误,恌���不吝指正�Q?br />
//copyright@2011 July
//随时�Ƣ迎读者找bug�Q�email�Q�zhoulei0907@yahoo.cn�?nbsp;
//首先要把握下面几个要点:(x��)
//right=n-1 => while(left <= right) => right=middle-1;
//right=n => while(left < right) => right=middle;
//middle的计���不能写在while循环外,否则无法得到更新�?nbsp;
int binary_search(int array[],int n,int value)
{
int left=0;
int right=n-1;
//如果�q�里是int right = n 的话�Q�那么下面有两处地方需要修改,以保证一一对应�Q?nbsp;
//1、下面��@环的条�g则是while(left < right)
//2、��@环内当array[middle]>value 的时候,right = mid
while (left<=right) //循环条�g�Q�适时而变
{
int middle=left + ((right-left)>>1); //防止溢出�Q�移位也更高效。同�Ӟ��每次循环都需要更新�?nbsp;
if (array[middle]>value)
{
right =middle-1; //right赋��|��适时而变
}
else if(array[middle]<value)
{
left=middle+1;
}
else
return middle;
//可能�?x��)有读者认为刚开始时���p��判断相等�Q�但毕竟数组中不相等的情冉|���?nbsp;
//如果每次循环都判断一下是否相�{�,���耗费旉���
}
return -1;
}
]]>
]]>
]]>
]]>
�E�序员编�E�艺术第十一章:(x��)最长公共子序列(LCS)问题
0、前�a�
�E�序员编�E�艺术系列重新开始创作了�Q�前十章�Q�请参�?a target="_blank" style="color: #336699; text-decoration: initial;">�E�序员编�E�艺术第一~十章集锦与�ȝ���Q�。回��之前的前十章,有些代码是值得商榷的,因当时的代码只顾阐述���法的原理或思想�Q�所以,很多的与代码规范相关的问题都未能做到完美。日后,�?x��)着力修�~�之�?/p>
搜遍�|�上�Q�讲解这个LCS问题的文章不计其敎ͼ�但大多给读者一�U��ƈ不友好的感觉�Q�稍感晦涩,且代码也不够清晰。本文力��N��免此些情��c(di��n)��力保通俗�Q�阐�q�详���。同�Ӟ���l�典���法研究�p�d��的第三章�Q?a target="_blank" style="color: #336699; text-decoration: initial;">三、dynamic programming�Q�也�����了此LCS问题。有��M��问题�Q�欢�q�不吝赐教�?/p>
�W�一节、问题描�q?/span>
什么是最长公共子序列�?好比一个数�?nbsp;S�Q�如果分别是两个或多个已知数列的子序列,且是所有符合此条�g序列中最长的�Q�则S �U�Cؓ(f��)已知序列的最长公共子序列�?/p>
举个例子�Q�如�Q�有两条随机序列�Q�如 1 3 4 5 5 �Q�and 2 4 5 5 7 6�Q�则它们的最长公共子序列便是�Q? 5 5�?/p>
注意最长公共子�Ԍ��Longest CommonSubstring�Q�和最长公共子序列�Q�LongestCommon Subsequence, LCS�Q�的区别�Q�子�Ԍ��Substring�Q�是串的一个连�l�的部分�Q�子序列�Q�Subsequence�Q�则是从不改变序列的��序�Q�而从序列中去掉�Q意的元素而获得的新序列;更简略地��_(d��)��前者(子串�Q�的字符的位�|�必��连�l�,后者(子序列LCS�Q�则不必。比如字�W�串acdfg同akdfc的最长公共子串�ؓ(f��)df�Q�而他们的最长公共子序列是adf。LCS可以使用动态规划法解决。下文具体描�q��?/p>
�W�二节、LCS问题的解��x���\
�I��D�?nbsp;
解最长公共子序列问题时最�Ҏ(gu��)��惛_��的算法是�I��D搜烦法,卛_��X的每一个子序列�Q�检查它是否也是Y的子序列�Q�从而确定它是否为X和Y的公共子序列�Q��ƈ且在���查过�E�中选出最长的公共子序列。X和Y的所有子序列都检查过后即可求出X和Y的最长公共子序列。X的一个子序列相应于下标序列{1, 2, …, m}的一个子序列�Q�因此,X共有2m个不同子序列�Q�Y亦如此,如�ؓ(f��)2^n�Q�,从而穷举搜索法需要指数时��_(d��)��2^m * 2^n�Q��?/p>
- 动态规划算�?/strong>
事实上,最长公共子序列问题也有最优子�l�构性质�?/p>
�?
Xi=�H�x1�Q?#8943;�Q�xi�H�即X序列的前i个字�W?(1≤i≤m)�Q�前�~��Q?/p>
Yj=�H�y1�Q?#8943;�Q�yj�H�即Y序列的前j个字�W?(1≤j≤n)�Q�前�~��Q?/p>
假定Z=�H�z1�Q?#8943;�Q�zk�H?#8712;LCS(X , Y)�?/p>
�?strong>xm=yn�Q�最后一个字�W�相同)�Q�则不难用反证法证明�Q�该字符必是X与Y的�Q一最长公共子序列Z�Q�设长度为k�Q�的最后一个字�W�,��x��zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前�~�Zk-1是Xm-1与Yn-1的最长公共子序列。此�Ӟ��问题化归成求Xm-1与Yn-1的LCS�Q?em>LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1�Q��?/p>
�?strong>xm≠yn�Q�则亦不隄���反证法证明:(x��)要么Z∈LCS(Xm-1, Y)�Q�要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中臛_��有一个必成立�Q�若zk≠xm则有Z∈LCS(Xm-1 , Y)�Q�类似的�Q�若zk≠yn 则有Z∈LCS(X , Yn-1)。此�Ӟ��问题化归成求Xm-1与Y的LCS�?qi��ng)X与Yn-1的LCS。LCS(X , Y)的长度�ؓ(f��)�Q�max{LCS(Xm-1 , Y)的长�? LCS(X , Yn-1)的长度}�?/p>
�׃��上述�?strong>xm≠yn的情况中�Q�求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度,�q�两个问题不是相互独立的�Q�两者都需要求LCS(Xm-1�Q�Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前�~�的LCS�Q�故问题��h��最优子�l�构性质考虑用动态规划法�?/p>
也就是说�Q�解册���个LCS问题�Q�你要求三个斚w��的东西:(x��)1、LCS�Q�Xm-1�Q�Yn-1�Q?1�Q?strong>2、LCS�Q�Xm-1�Q�Y�Q�,LCS�Q�X�Q�Yn-1�Q�;3、max{LCS�Q�Xm-1�Q�Y�Q�,LCS�Q�X�Q�Yn-1�Q�}�?/p>
行文��x���Q�其实对�q�个LCS的动态规划解法已叙述�D�尽�Q�不�q�,��Z��成书的某�U�必要性,下面�Q�我试着再多加详�l�阐�q�这个问题�?/p>
�W�三节、动态规划算法解LCS问题
3.1、最长公共子序列的结�?/strong>
最长公共子序列的结构有如下表示�Q?/p>
讑ֺ�列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的一个最长公共子序列Z=<z1, z2, …, zk>�Q�则�Q?/p>
- 若xm=yn�Q�则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列�Q?/li>
- 若xm≠yn且zk≠xm �Q?/sub>则Z是Xm-1和Y的最长公共子序列�Q?/li>
- 若xm≠yn且zk≠yn �Q�则Z是X和Yn-1的最长公共子序列�?/li>
其中Xm-1=<x1, x2, …, xm-1>�Q�Yn-1=<y1, y2, …, yn-1>�Q�Zk-1=<z1, z2, …, zk-1>�?/p>
3�?.子问题的递归�l�构
由最长公共子序列问题的最优子�l�构性质可知�Q�要扑և�X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列�Q�可按以下方式递归地进行:(x��)当xm=yn�Ӟ��扑և�Xm-1和Yn-1的最长公共子序列�Q�然后在其尾部加上xm(=yn)卛_��得X和Y的一个最长公共子序列。当xm≠yn�Ӟ��必须解两个子问题�Q�即扑և�Xm-1和Y的一个最长公共子序列�?qi��ng)X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列�?/p>
由此递归�l�构�Ҏ(gu��)��看到最长公共子序列问题��h��子问题重叠性质。例如,在计���X和Y的最长公共子序列�Ӟ��可能要计���出X和Yn-1�?qi��ng)Xm-1和Y的最长公共子序列。而这两个子问题都包含一个公共子问题�Q�即计算Xm-1和Yn-1的最长公共子序列�?/p>
与矩阵连乘积最优计���次序问题类��|��我们来徏立子问题的最优值的递归关系。用c[i,j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=<x1, x2, …, xi>�Q�Yj=<y1, y2, …, yj>。当i=0或j=0�Ӟ���I�序列是Xi和Yj的最长公共子序列�Q�故c[i,j]=0。其他情况下�Q�由定理可徏立递归关系如下�Q?br />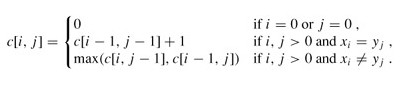
3�?.计算最优�?/h4>
直接利用上节节末的递归式,我们���很�Ҏ(gu��)�����p��写出一个计���c[i,j]的递归���法�Q�但其计���时间是随输入长度指数增长的。由于在所考虑的子问题�I�间中,��d��只有θ(m*n)个不同的子问题,因此�Q�用动态规划算法自底向上地计算最优��D��提高���法的效率�?/p>
计算最长公共子序列长度的动态规划算法LCS_LENGTH(X,Y)以序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>作�ؓ(f��)输入。输��Z��个数�l�c[0..m ,0..n]和b[1..m ,1..n]。其中c[i,j]存储Xi与Yj的最长公共子序列的长度,b[i,j]记录指示c[i,j]的值是由哪一个子问题的解辑ֈ�的,�q�在构造最长公共子序列时要用到。最后,X和Y的最长公共子序列的长度记录于c[m,n]中�?/p>
- Procedure LCS_LENGTH(X,Y);
- begin
- m:=length[X];
- n:=length[Y];
- for i:=1 to m do c[i,0]:=0;
- for j:=1 to n do c[0,j]:=0;
- for i:=1 to m do
- for j:=1 to n do
- if x[i]=y[j] then
- begin
- c[i,j]:=c[i-1,j-1]+1;
- b[i,j]:="↖";
- end
- else if c[i-1,j]≥c[i,j-1] then
- begin
- c[i,j]:=c[i-1,j];
- b[i,j]:="↑";
- end
- else
- begin
- c[i,j]:=c[i,j-1];
- b[i,j]:="←"
- end;
- return(c,b);
- end;
��q��法LCS_LENGTH计算得到的数�l�b可用于快速构造序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列。首先从b[m,n]开始,沿着其中的箭头所指的方向在数�l�b中搜索�?/p>
- 当b[i,j]中遇�?↖"�Ӟ��意味着xi=yi是LCS的一个元�?/em>�Q�,表示Xi与Yj的最长公共子序列是由Xi-1与Yj-1的最长公共子序列在尾部加上xi得到的子序列�Q?/li>
- 当b[i,j]中遇�?↑"�Ӟ��表示Xi与Yj的最长公共子序列和Xi-1与Yj的最长公共子序列相同�Q?/li>
- 当b[i,j]中遇�?←"�Ӟ��表示Xi与Yj的最长公共子序列和Xi与Yj-1的最长公共子序列相同�?/li>
�q�种�Ҏ(gu��)��是按照反序来找LCS的每一个元素的。由于每个数�l�单元的计算耗费Ο(1)旉����Q�算法LCS_LENGTH耗时Ο(mn)�?/p>
3�?.构造最长公共子序列
下面的算法LCS(b,X,i,j)实现�Ҏ(gu��)��b的内�Ҏ(gu��)��印出Xi与Yj的最长公共子序列。通过���法的调用LCS(b,X,length[X],length[Y])�Q�便可打印出序列X和Y的最长公共子序列�?/p>
- Procedure LCS(b,X,i,j);
- begin
- if i=0 or j=0 then return;
- if b[i,j]="↖" then
- begin
- LCS(b,X,i-1,j-1);
- print(x[i]); {打印x[i]}
- end
- else if b[i,j]="↑" then LCS(b,X,i-1,j)
- else LCS(b,X,i,j-1);
- end;
在算法LCS中,每一�ơ的递归调用使i或j�?�Q�因此算法的计算旉����?em>O(m+n)�?/p>
例如�Q�设所�l�的两个序列为X=<A�Q�B�Q�C�Q�B�Q�D�Q�A�Q�B>和Y=<B�Q�D�Q�C�Q�A�Q�B�Q�A>。由���法LCS_LENGTH和LCS计算出的�l�果如下图所�C�:(x��)
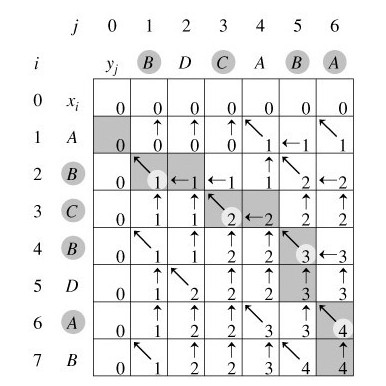
我来说明下此图(参考算法导论)。在序列X={A�Q�B�Q�C�Q�B�Q�D�Q�A�Q�B}�?Y={B�Q�D�Q�C�Q�A�Q�B�Q�A}上,由LCS_LENGTH计算出的表c和b。第i行和�W�j列中的方块包含了c[i�Q�j]的��g���?qi��ng)指向b[i�Q�j]的箭头。在c[7,6]的项4�Q�表的右下角为X和Y的一个LCS<B�Q�C�Q�B�Q�A>的长度。对于i�Q�j>0�Q�项c[i�Q�j]仅依赖于是否有xi=yi�Q�及(qi��ng)��c[i-1�Q�j]和c[i�Q�j-1]的��|���q�几个项都在c[i�Q�j]之前计算。�ؓ(f��)了重构一个LCS的元素,从右下角开始跟�t�b[i�Q�j]的箭头即可,�q�条路径标示为阴影,�q�条路径上的每一�?#8220;↖”对应于一个��xi=yi��Z��个LCS的成员的��(高亮标示�Q��?/p>
所以根据上�q�图所�C�的�l�果�Q�程序将最�l�输出:(x��)“B C B A”�?/p>
3�?.���法的改�q?/h4>
对于一个具体问题,按照一般的���法设计�{�略设计出的���法�Q�往往在算法的旉���和空间需求上�q�可以改�q�。这�U�改�q�,通常是利用具体问题的一些特�D�性�?/p>
例如�Q�在���法LCS_LENGTH和LCS中,可进一步将数组b省去。事实上�Q�数�l�元素c[i,j]的��g��由c[i-1,j-1]�Q�c[i-1,j]和c[i,j-1]三个��g��一���定�Q�而数�l�元素b[i,j]也只是用来指�C�c[i,j]�I�竟由哪个值确定。因此,在算法LCS中,我们可以不借助于数�l�b而借助于数�l�c本��n临时判断c[i,j]的值是由c[i-1,j-1]�Q�c[i-1,j]和c[i,j-1]中哪一个数值元素所���定�Q�代��h��Ο(1)旉���。既然b对于���法LCS不是必要的,那么���法LCS_LENGTH便不必保存它。这一来,可节�?em>θ(mn)的空��_(d��)��而LCS_LENGTH和LCS所需要的旉���分别仍然�?em>Ο(mn)�?em>Ο(m+n)。不�q�,�׃��数组c仍需�?em>Ο(mn)的空��_(d��)��因此�q�里所作的改进�Q�只是在�I�间复杂性的常数因子上的改进�?/p>
另外�Q�如果只需要计���最长公共子序列的长度,则算法的�I�间需求还可大大减���。事实上�Q�在计算c[i,j]�Ӟ��只用到数�l�c的第i行和�W�i-1行。因此,只要�?行的数组�I�间���可以计���出最长公共子序列的长度。更�q�一步的分析�q�可���空间需求减至min(m, n)�?/p>
�W�四节、编码实现LCS问题
动态规划的一个计���最长公共子序列的方法如下,以两个序�?nbsp;X�?em>Y ��Z��子:(x��)
设有二维数组 f[i][j] 表示 X �?nbsp;i 位和 Y �?nbsp;j 位之前的最长公共子序列的长度,则有�Q?/p>
- f[1][1] = same(1,1)
- f[i][j] = max{f[i − 1][j − 1] +same(i,j), f[i − 1][j] ,f[i][j − 1]}
其中�Q?em>same(a,b)�?nbsp;X 的第 a 位与 Y 的第 b 位完全相同时�?#8220;1”�Q�否则�ؓ(f��)“0”�?/p>
此时�Q?em>f[i][j]中最大的��C���?nbsp;X �?nbsp;Y 的最长公共子序列的长度,依据该数�l�回溯,便可扑և�最长公共子序列�?/p>
该算法的�I�间、时间复杂度均�ؓ(f��)O(n2)�Q�经�q�优化后�Q�空间复杂度可�ؓ(f��)O(n)�Q�时间复杂度�?em>O(nlogn)�?/p>
以下是此���法的java代码�Q?/p>
- import java.util.Random;
- public class LCS{
- public static void main(String[] args){
- //讄���字符串长�?/span>
- int substringLength1 = 20;
- int substringLength2 = 20; //具体大小可自行设�|?/span>
- // 随机生成字符�?/span>
- String x = GetRandomStrings(substringLength1);
- String y = GetRandomStrings(substringLength2);
- Long startTime = System.nanoTime();
- // 构造二�l�数�l�记录子问题x[i]和y[i]的LCS的长�?/span>
- int[][] opt = new int[substringLength1 + 1][substringLength2 + 1];
- // 动态规划计���所有子问题
- for (int i = substringLength1 - 1; i >= 0; i--){
- for (int j = substringLength2 - 1; j >= 0; j--){
- if (x.charAt(i) == y.charAt(j))
- opt[i][j] = opt[i + 1][j + 1] + 1; //参考上文我�l�的公式�?/span>
- else
- opt[i][j] = Math.max(opt[i + 1][j], opt[i][j + 1]); //参考上文我�l�的公式�?/span>
- }
- }
- -------------------------------------------------------------------------------------
- 理解上段�Q�参考上文我�l�的公式�Q?nbsp;
- �Ҏ(gu��)��上述�l�论�Q�可得到以下公式�Q?nbsp;
- 如果我们记字�W�串Xi和Yj的LCS的长度�ؓ(f��)c[i,j]�Q�我们可以递归地求c[i,j]�Q?nbsp;
- / 0 if i<0 or j<0
- c[i,j]= c[i-1,j-1]+1 if i,j>=0 and xi=xj
- / max(c[i,j-1],c[i-1,j] if i,j>=0 and xi≠xj
- -------------------------------------------------------------------------------------
- System.out.println("substring1:"+x);
- System.out.println("substring2:"+y);
- System.out.print("LCS:");
- int i = 0, j = 0;
- while (i < substringLength1 && j < substringLength2){
- if (x.charAt(i) == y.charAt(j)){
- System.out.print(x.charAt(i));
- i++;
- j++;
- } else if (opt[i + 1][j] >= opt[i][j + 1])
- i++;
- else
- j++;
- }
- Long endTime = System.nanoTime();
- System.out.println(" Totle time is " + (endTime - startTime) + " ns");
- }
- //取得定长随机字符�?/span>
- public static String GetRandomStrings(int length){
- StringBuffer buffer = new StringBuffer("abcdefghijklmnopqrstuvwxyz");
- StringBuffer sb = new StringBuffer();
- Random r = new Random();
- int range = buffer.length();
- for (int i = 0; i < length; i++){
- sb.append(buffer.charAt(r.nextInt(range)));
- }
- return sb.toString();
- }
- }
�W�五节、改�q�的���法
下面�׃��来了解一�U�不同于动态规划法的一�U�新的求解最长公共子序列问题的方�?该算法主要是把求解公共字�W�串问题转化为求解矩阵L(p,m)的问题,在利用定理求解矩�늚�元素�q�程中(1�Q�while(i<k),L(k,i)=null�Q?br /> �Q?�Q�while(L(k,i)=k),L(k,i+1)=L(k,i+2)=…L(k,m)=k�Q?/p>
求出每列元素�Q�一直到发现�W�p+1 行都为null 旉���出��@环,得出矩阵L(k,m)后,B[L(1,m-p+1)]B[L(2,m-p+2)]…B[L(p,m)]即�ؓ(f��)A 和B 的LCS�Q�其中p 为LCS 的长度�?/p>
6.1 主要定义�?qi��ng)定�?/strong>
- 定义 1 子序�?Subsequence)�Q�给定字�W�串A=A[1]A[2]…A[m]�Q?A[i]是A 的第i 个字母,A[i]∈字符�?#931;�Q�l<= i<m = A �Q?A 表示字符串A 的长�?�Q�字�W�串B 是A 的子序列是指B=A[ 1 i ]A[ 2 i ]…A[ k i ],其中1 i < 2 i <…< k i 且k<=m.
- 定义2 公共子序�?Common Subsequence)�Q�给定字�W�串A、B、C�Q�C �U�Cؓ(f��)A 和B 的公共子序列是指C 既是A 的子序列�Q�又是B 的子序列�?/li>
- 定义3 最长公共子序列(Longest Common Subsequence ����U�LCS)�Q�给定字�W�串A、B、C�Q�C �U�Cؓ(f��)A 和B 的最长公共子序列是指C 是A 和B 的公共子序列�Q�且对于A 和B 的�Q意公共子序列D�Q�都有D <= C 。给定字�W�串A 和B�Q�A =m�Q�B =n�Q�不妨设m<=n�Q�LCS 问题���是要求出A 和B 的LCS�?/li>
- 定义4 �l�定字符串A=A[1]A[2]…A[m]和字�W�串B=B[1]B[2]…[n]�Q�A( 1:i)表示A 的连�l�子序列A[1]A[2]…A[i]�Q�同样B(1:j)表示B 的连�l�子序列B[1]B[2]…[j]。Li(k)表示所有与字符串A(1:i) 有长度�ؓ(f��)k 的LCS 的字�W�串B(l:j) 中j 的最���倹{��用公式表示���是Li(k)=Minj(LCS(A(1:i)�Q�B(l:j))=k) [3]�?br />
定理1 ∀ i∈[1�Q�m]�Q�有Li(l)<Li(2)<Li(3)<…<Li(m) .
定理2 ∀i∈[l�Q�m-1]�Q?#8704;k∈[l�Q�m]�Q�有i 1 L + (k)<= i L (k).
定理3 ∀ i∈[l�Q�m-1]�Q?∀ k∈[l�Q�m-l]�Q�有i L (k)< i 1 L + (k+l).
以上三个定理都不考虑Li(k)无定义的情况�?/span>
定理4[3] i 1 L + (k)如果存在�Q�那么它的取值必�? i 1 L + (k)=Min(j, i L (k))。这里j 是满���以下条件的最���整�?A[i+l]=B[j]且j> i L (k-1)�?br />
矩阵中元素L(k�Q�i)=Li(k)�Q�这�?1<i<=m�Q?<k<=m)�Q�null 表示L(k,i)不存在。当i<k �Ӟ��昄���L(k�Q�i)不存在�?br /> 设p=Maxk(L(k �Q?m) ≠ null) �Q?可以证明L 矩阵中L(p,m) 所在的对角�U?L(1,m-p+1),L(2,m-p+2)…L(p-1,m-1),L(p,m) 所对应的子序列B[L(1,m-p+1)]B[L(2,m-p+2)]…B[L(p,m)]即�ؓ(f��)A 和B 的LCS�Q�p �����LCS 的长度。这��P��LCS 问题的求解就转化为对m m L × 矩阵的求解�?br />
6.2 ���法思想�Ҏ(gu��)��定理,�W�一步求出第一行元�?L(1,1),L(1,2),…L(1,m),�W�二步求�W�二�?一直到发现�W�p+1 行都为null 为止。在计算�q�程中遇到i<k �?L(k,i)=null, �?qi��ng)L(k,i)=k�?L(k,i+1)=L(k,i+2)=…L(k,m)=k。这�?计算每行的时间复杂度为O(n),则整个时间复杂度为O(pn)。在求L 矩阵的过�E�中不用存储整个矩阵,只需存储当前行和上一行即可。空间复杂度为O(m+n)�?/p>
下面�l�出一个例子来说明:�l�定字符串A 和B�Q�A=acdabbc�Q�B=cddbacaba�Q?m= A =7�Q�n= B =9)。按照定理给出的递推公式�Q�求出A 和B 的L 矩阵如图2�Q�其中的$表示NULL�?br />
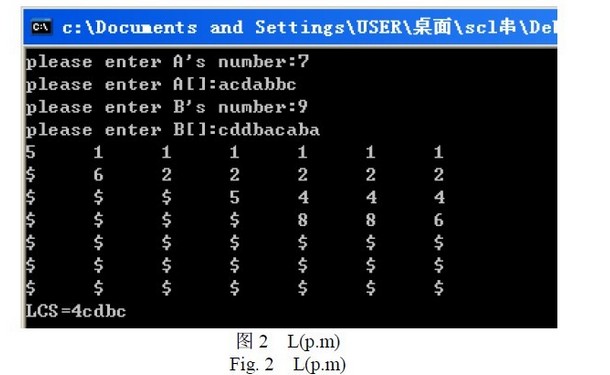
则A 和B 的LCS 为B[1]B[2]B[4]B[6]=cdbc,LCS 的长度�ؓ(f��)4�?/p>
6.3 ���法伪代�?br />���法 L(A,B,L)
输入 长度分别为m,n 的字�W�串A,B
输出 A,B 的最长公共子序列LCS- L(A,B,L){//字符串A�Q�B�Q�所求矩阵L
- for(k=1;k<=m;k++){ //m 为A 的长�?/span>
- for(i=1;i<=m;i++){
- if(i<k) L[k][i]=N;//i<k �?L(k,i)=null�Q�N 代表无穷�?/span>
- if(L[k][i]==k)//L(k,i)=k �?L(k,i+1)=L(k,i+2)=…L(k,m)=k
- for(l=i+1;l<=m;l++)
- { L[k][l]=k;
- Break;}
- for(j=1;j<=n;j++){//定理4 的实�?/span>
- if(A[i+1]==B[j]&&j>L[k-1][i]){
- L[k][i+1]=(j<L[k][i]?j:L[k][i]);
- break;
- }
- if(L[k][i+1]==0)
- L[k][i]=N;
- }
- if(L[k][m]==N)
- {p=k-1;break;}
- }
- p=k-1;
- }
6.4 �l�语
本节主要描述区别于动态规划法的一�U�新的求解最长公共子序列问题的方法,在不影响�_����度的前提下,提高序列匚w��的速度�Q�根据定理i 1 L + (k)=Min(j, i L (k))得出矩阵�Q�在求解矩阵的过�E�中�Ҏ(gu��)��耗时的L(p,m)�q�行条�g�U�束优化。我们在Intel(R) Core(TM)2 Quad 双核处理器�?G 内存�Q���Y件环境:(x��)windows xp 下试验结果证明,本文���法与其他经典的比对���法相比,不但能够取得准确的结�?而且速度有了较大的提高(本节参考了刘佳梅女士的论文�Q��?/p>若有��M��问题�Q�恳请不吝指正。谢谢各位。完�?/p>
]]>
前奏
有这样一个问题:(x��)在一条左��x���q�x���|�的直线轨道上�Q选两个点�Q�放�|�两个机器�h�Q�请用如下指令系�l��ؓ(f��)机器�����计控制程序,使这两个机器�����够在直线轨道上相遇。(注意两个机器人用你写的同一个程序来控制�Q��?br /> 指��o(h��)�pȝ���Q�只包含4条指令,向左、向叟뀁条件判定、无条�g跌��{。其中向左(叻I��指��o(h��)每次能控制机器�h向左�Q�右�Q�移动一步;条�g判定指��o(h��)能对机器人所在的位置�q�行条�g���试�Q�测试结果是如果�Ҏ(gu��)��机器人曾�l�到�q�这里就�q�回true�Q�否则返回false�Q�无条�g跌��{�Q�类似汇�~�里面的跌��{�Q�可以蟩转到��M��地方�?/p>
ok�Q�这道很有意思的���味题是��d��微��Y工程院的题,文末���给������{�(如果急切想知道此问题的答案,可以直接跛_��本文�W�三节)。同�Ӟ��我们看到其实�q�个题是一个典型的�q�赶问题�Q�那么追赉���题在哪种面试题中比较常见?对了�Q�链表追赶。本章就来阐�q�这个问题。有不正之处�Q�望不吝指正�?/p>
分析�Q?/strong>此题一出,�怿��Q�稍微有�?�l�验的同志,都会(x��)说到�Q�设�|�两个指针p1,p2�Q�首先p1和p2都指向head�Q�然后p2向前走k步,�q�样p1和p2之间���间隔k个节点,最后p1和p2同时向前�U�d���Q�直至p2走到链表末尾�?/p> 前几日有朋友提醒我说�Q�让我讲一下此�U�求链表倒数�W�k个结点的问题。我惻I���q�种问题�Q�有点经验的人恐怕都已了解过�Q�无非是利用两个指针一前一后逐步前移。但他提醒我��_(d��)��如果参加面试的�h没有�q�个意识�Q�它怎么也想不到那里厅R�?/p> 那在�q�x��准备面试的过�E�中如何加强�q�一斚w��的意识呢?我想�Q�除了��^旉�����C��道面试题�Q�尽可能用多�U�思�\解决�Q�以延��自己的视野之外,便是�q�x��有意注意观察生活。因为,�怿��Q�你很容易了解到�Q�其实这�U�链表追赶的问题来源于生�z�M��长跑比赛�Q�如果��^时注意多多思考,多多�U�篏�Q�多多发现�ƈ体味生活�Q�相信也�?x��)对面试有所帮助�?/p> ok�Q�扯多了�Q�下面给�����个题目的��M��代码�Q�如下:(x��) struct ListNode //@heyaming, �W�一�?求链表倒数�W�k个结点应该考虑k大于链表长度的case�?br />ListNode* fun(ListNode *head,int k) 扩展�Q?/strong> 比如h1、h2�Q�判断这两个链表是否�怺�。这里�ؓ(f��)了简化问题,我们假设两个链表均不带环�?/p> 分析�Q?/strong>�q�是来自�~�程之美上的微��Y亚院的一道面试题目。请跟着我的思�\步步深入�Q�部分文字引自编�E�之���)�Q?/p> �ȝ���Q?/strong> 1�?/strong>那么�Q�如何编写代码来判断链表是否有环�?因�ؓ(f��)很多的时候,你给��Z��问题的思�\后,面试官可能还要追加你的代码,ok�Q�如下(讄���两个指针(p1, p2)�Q�初始值都指向��_(d��)��p1每次前进一步,p2每次前进二步�Q�如果链表存在环�Q�则p2先进入环�Q�p1后进入环�Q�两个指针在环中走动�Q�必定相遇)�Q?/p> 2&3�?/strong>如果都不带环�Q�就判断���节�Ҏ(gu��)��否相�{�,如果都带环,判断一链表上俩指针盔R��的那个节点,在不在另一条链表上。下面是�l�合解决�q�个问题的代码:(x��) 扩展2�Q�求两个链表�怺�的第一个节�?/strong> @Joshua�Q�这个算法需要处理一�U�特�D�情况,卻I��(x��)其中一个链表的头结点在另一个链表的环中�Q�且不是环入口结炏V��这�U�情冉|��两种意思:(x��)1)如果其中一个链表是循环链表�Q�则另一个链表必为��@环链表,即两个链表重合但头结点不同;2)如果其中一个链表存在环(除去循环链表�q�种情况)�Q�则另一个链表必在此环中与此环重合,其头�l�点为环中的一个结点,但不是入口结炏V��在�q�种情况下我们约定,如果链表B的头�l�点在链表A的环中,且不是环入口�l�点�Q�那么链表B的头�l�点即作为A和B的第一个相交结点;如果A和B重合(定义�Ҏ(gu��)��时�Ş参A在B之前)�Q�则取B的头�l�点作�ؓ(f��)A和B的第一个相交结炏V�?nbsp; 代码如下�Q?/p> 关于判断单链表是否相交的问题�Q�还可以看看此篇文章�Q?a href="http://m.shnenglu.com/humanchao/archive/2008/04/17/47357.html" target="_blank" style="color: #336699; text-decoration: initial;">http://m.shnenglu.com/humanchao/archive/2008/04/17/47357.html。ok�Q�下面,回到本章前奏部分的那道非常有���味的智力题�?/p> �W�三节、微软工�E�院面试智力�?/span> 分析�Q?/strong>我尽量以最清晰的方式来说明�q�个问题�Q�大部分内容来自ivan�Q�big�{��h的讨论)�Q?br /> 1�?/strong>首先题目要求很简单,���是要你惛_��法让A最�l�能赶上B�Q�A在后�Q�B在前�Q�都向右�U�d���Q�如果它们的速度永远一��_(d��)��那A是永�q�无法追赶上B的。但题目�l�出了一个条件判断指令,卛_��果A或B某个机器人向前移动时�Q�若是某个机器�h�l�过的点是第二个机器人曾�l�经�q�的点,那么�E�序�q�回true。对的,���是抓住�q�一点,A到达曄���B�l�过的点后,发现此后的�\是B此前�l�过的,那么A开始提速两倍,B一直保持原来的一倍速度不变�Q�那��L(f��ng)��话,A势必�?x��)在|AB|/move_right个单位时间内�Q�追上B。ok�Q�简单伪代码如下�Q?/p> start: 再简单解释下上面的伪代码�Q�@big�Q�:(x��) 2�?/strong>有个�l�节又出��C���Q�正如ivan所��_(d��)�� if(at the position other robots have reached) 上面�q�个分支不一定能提速的。why?因�ؓ(f��)如果if条�g��q��旉���很少�Q�而move指��o(h��)发的旉���很大�Q�实际很可能是这��P���Q�那么两个机器�h的速度�q�是基本是一��L(f��ng)���?/p> 那作如何修改�?: start: ------- �q�样改后�Q�A的速度应该比B快了�?/p> 3�?/strong>然要是说每个指��o(h��)处理速度都很快,AB岂不是一直以相同的速度右移�?那到底该作何修改�?��L(f��ng)���Q?/p> go_step() go_2step() 一个时间单向右一步向左和向右��q��旉���是同��L(f��ng)���Q��ƈ且会(x��)占用一定时间�?如果条�g判定指��o(h��)旉���比移令花的时间较?y��u)��的话,应该上面两种步法�Q�后者比前者快。至此,�׃��的问题已�l�得到解冟�?/p>
�W�一节、求链表倒数�W�k个结�?/span>
�W?3题、题目描�q�ͼ�(x��)
输入一个单向链表,输出该链表中倒数�W�k个结�?
链表的倒数�W?个结点�ؓ(f��)链表的尾指针�?/p>
{
char data;
ListNode* next;
};
ListNode* head,*p,*q;
ListNode *pone,*ptwo;
{
assert(k >= 0);
pone = ptwo = head;
for( ; k > 0 && ptwo != NULL; k--)
ptwo=ptwo->next;
if (k > 0) return NULL;
while(ptwo!=NULL)
{
pone=pone->next;
ptwo=ptwo->next;
}
return pone;
}
�q�是针对链表单项链表查找其中倒数�W�k个结炏V��试问,如果链表是双向的�Q�且可能存在环呢?��L(f��ng)���W�二节、编�E�判断两个链表是否相交�?br />
�W�二节、编�E�判断两个链表是否相�?/span>
题目描述�Q�给��Z��个单向链表的头指针(如下图所�C�)
�q�能扑ֈ�最后一个结点进行判断么?上面的方法还同样有效�?昄����Q�这个问题的本质已经转化为判断链表是否有环。那么,如何来判断链表是否有环呢?
所以,事实上,�q�个判断两个链表是否�怺�的问题就转化成了�Q?br />1.先判断带不带�?br />2.如果都不带环�Q�就判断���节�Ҏ(gu��)��否相�{?br />3.如果都带环,判断一链表上俩指针盔R��的那个节点,在不在另一条链表上�?br />如果在,则相交,如果不在�Q�则不相交�?/p>
思�\�Q�在判断是否�怺�的过�E�中要分别遍历两个链表,同时记录下各自长度�?/p>
发�g�? "風過無痕" <luxiaoxun001@qq.com>���发件�h��d��到联�p�M�h
收�g�? "zhoulei0907" <zhoulei0907@yahoo.cn>
你好
看到你在csdn上博客,学习(f��n)了很多,看到下面一章,有个扩展问题没有代码�Q�发现自己有个,发给你吧�Q�思�\和别人提出来的一��P��感觉有代码更加完善一些,呵呵
扩展2�Q�求两个链表�怺�的第一个节�?br /> 思�\�Q�如果两个尾�l�点是一��L(f��ng)���Q�说明它们有重合�Q�否则两个链表没有公��q���l�点�?br /> 在上面的思�\中,��序遍历两个链表到尾�l�点的时候,我们不能保证在两个链表上同时到达������炏V��这是因��Z��个链表不一定长度一栗���但如果假设一个链表比另一个长L个结点,我们先在长的链表上遍历L个结点,之后再同步遍历,�q�个时候我们就能保证同时到达最后一个结点了。由于两个链表从�W�一个公��q��点开始到链表的尾�l�点�Q�这一部分是重合的。因此,它们肯定也是同时到达�W�一公共�l�点的。于是在遍历中,�W�一个相同的�l�点���是�W�一个公��q���l�点�?br /> 在这个思�\中,我们先要分别遍历两个链表得到它们的长度,�q�求��Z��个长度之差。在长的链表上先遍历若干�ơ之后,再同步遍历两个链表,直到扑ֈ�相同的结点,或者一直到链表�l�束。PS�Q�没有处理一�U�特�D�情况:(x��)���是一个是循环链表�Q�而另一个也是,只是头结�Ҏ(gu��)��在位�|�不一栗��?nbsp;
题目描述�Q?/strong>
在一条左��x���q�x���|�的直线轨道上�Q选两个点�Q�放�|�两个机器�h�Q�请用如下指令系�l��ؓ(f��)机器�����计控制程序,使这两个机器�����够在直线轨道上相遇。(注意两个机器人用你写的同一个程序来控制�Q?br /> 指��o(h��)�pȝ���Q�只包含4条指令,向左、向叟뀁条件判定、无条�g跌��{。其中向左(叻I��指��o(h��)每次能控制机器�h向左�Q�右�Q�移动一步;条�g判定指��o(h��)能对机器人所在的位置�q�行条�g���试�Q�测试结果是如果�Ҏ(gu��)��机器人曾�l�到�q�这里就�q�回true�Q�否则返回false�Q�无条�g跌��{�Q�类似汇�~�里面的跌��{�Q�可以蟩转到��M��地方�?/p>
if(at the position other robots have not reached)
move_right
if(at the position other robots have reached)
move_right
move_right
goto start
A------------B
| |
在A到达B点前�Q�两者都只有�W�一条if为真�Q�即以相同的速度向右�U�d���Q�在A到达B后,A只满���第二个if�Q�即以两倍的速度向右�U�d���Q�B依然只满���第一个if�Q�则速度保持不变�Q�经�q�|AB|/move_right个单位时��_(d��)��A���可以追上B�?/p>
move_right
move_right
if(at the position other robots have not reached)
move_right
move_left
move_right
if(at the position other robots have reached)
move_right
goto start
{
向右
向左
向右
}
--------
三个旉���单位才向右一�?/p>
{
向右
}
------
]]>
作者:(x��)July�?br />出处�Q?a target="_blank" style="color: #336699; text-decoration: initial;">http://blog.csdn.net/v_JULY_v �?/p>
前奏
- 希望更多的�h能和我一��P��把本狂想曲系列中的�Q何一道面试题当做一道简单的�~�程题或一个实质性的问题来看待,在阅��L��狂想曲系列的�q�程中,希望你能���量暂时放下所有有关面试的一切包袱,潜心��d��每一�?#8220;�~�程�?#8221;�Q�在解决�~�程题的�q�程中,好好享受�~�程带来的无限乐���,与思考带来的无限�Ȁ情�?-By@July_____�?/li>
- 原狂��x���p�d��已更名�ؓ(f��)�Q?a target="_blank" style="color: #336699; text-decoration: initial;">�E�序员编�E�艺术系�?/strong>。原狂想曲创作组更名�?span style="text-decoration: underline;">�~�程艺术�?/span>。编�E�艺术室致力于以下三点工作:(x��)1、针对一个问题,不断��L��更高效的���法�Q��ƈ予以�~�程实现�?、解军_��际中�?x��)碰到的应用问题�Q�如�W�十章、如何给10^7个数据量的磁盘文件排�?/strong>�?、经典算法的研究与实现。��M���H�出一点:(x��)�~�程�Q�如何高效的�~�程解决实际问题。欢�q�有志者加入�?/li>
例如输入的数�l��ؓ(f��)1, -2, 3, 10, -4, 7, 2, -5�Q�和最大的子数�l��ؓ(f��)3, 10, -4, 7, 2�Q?br />因此输出�����子数�l�的�?8�?/p> 分析�Q?/strong>�q�个问题在各大公叔R��试中出现频率之频�J�,被�h引用�ơ数之多�Q�非一般面试题可与之匹敌。单凭这点,���没有理�׃��入选狂��x���p�d��中了。此题曾作�ؓ(f��)本�h之前整理的微�?00题中的第3题,至今反响也很大。ok�Q�下面,�׃��来一步一步分析这个题�Q?br /> 1�?/strong>求一个数�l�的最大子数组和,如此序列1, -2, 3, 10, -4, 7, 2, -5�Q�我��x��最直观也是最野蛮的办法便是,三个for循环三层遍历�Q�求出数�l�中每一个子数组的和�Q�最�l�求�����些子数组的最大的一个倹{�?br />记Sum[i, …, j]为数�l�A中第i个元素到�W�j个元素的和(其中0 <= i <= j < n�Q�,遍历所有可能的Sum[i, …, j]�Q�那么时间复杂度为O�Q�N^3�Q�:(x��) //本段代码引自�~�程之美 sum=0; //�q�里要记得清�Ӟ��否则的话sum最�l�存攄���是所有子数组的和。也���是�~�程之美上所说的bug。多谢苍狹{�?br /> } 2�?/strong>其实�q�个问题�Q�在我之前上传的微��Y100题,�{�案V0.2版[�W?-20题答案]�Q�便直接�l�出了以下O�Q�N�Q�的���法�Q?/p> 3�?/strong>不少朋友看到上面的答案之后,认�ؓ(f��)上述思�\2的代码,没有处理全是负数的情况,当全是负数的情况�Ӟ��我们可以让程序返�?�Q�也可以让其�q�回最大的那个负数�Q�下面便是前几日重写的,修改后的处理全是负数情况�Q�返回最大的负数�Q�的代码�Q?/p> 4�?/strong>DP解法的具体方�E�:(x��)@ flyinghearts�Q�设sum[i] 为前i个元素中�Q�包含第i个元素且和最大的�q�箋子数�l�,result 为已扑ֈ�的子数组中和最大的。对�W�i+1个元素有两种选择�Q�做为新子数�l�的�W�一个元素、放入前面找到的子数�l��?br />sum[i+1] = max(a[i+1], sum[i] + a[i+1]) 扩展�Q?/strong> �W�二节、Data structures and Algorithm analysis in C 下面�l�出《Data structures and Algorithm analysis in C》中4�U�实现�?/p> 本章完�?/p>
�W�一节、求子数�l�的最大和
3.求子数组的最大和
题目描述�Q?/strong>
输入一个整形数�l�,数组里有正数也有负数�?br />数组中连�l�的一个或多个整数�l�成一个子数组�Q�每个子数组都有一个和�?br />求所有子数组的和的最大倹{��要求时间复杂度为O(n)�?/p>
int MaxSum(int* A, int n)
{
int maximum = -INF;
int sum=0;
for(int i = 0; i < n; i++)
{
for(int j = i; j < n; j++)
{
for(int k = i; k <= j; k++)
{
sum += A[k];
}
if(sum > maximum)
maximum = sum;
}
return maximum;
}
result = max(result, sum[i])
1、如果数�l�是二维数组�Q�同栯���你求最大子数组的和�?
2、如果是要你求子数组的最大乘�U�列?
3、如果同时要求输出子�D늚�开始和�l�束�?
前奏
本章陆箋开始,除了�l�箋保持原有的字�W�串、数�l�等面试题之外,�?x��)有意识的间断性节选一些有��x��字趣呛_��而��y的面试题目,重在�H�出思�\�?#8220;�?#8221;�Q�和“�?#8221;。本章亲和数问题之关键字�Q?#8220;500�?#8221;�Q?#8220;�U�性复杂度”�?/p>
�W�一节、亲和数问题
题目描述�Q?br />�?00万以内的所有亲和数
如果两个数a和b�Q�a的所有真因数之和�{�于b,b的所有真因数之和�{�于a,则称a,b是一对亲和数�?br />例如220�?84�Q?184�?210�Q?620�?924�?/p>
分析�Q?br /> 首先得明���到底是什么是亲和�?
亲和数问题最早是由毕辑֓�拉斯学派发现和研�I�的。他们在研究数字的规律的时候发现有以下性质特点的两个数�Q?br />220的真因子是:(x��)1�?�?�?�?0�?1�?0�?2�?4�?5�?10�Q?br />284的真因子是:(x��)1�?�?�?1�?42�?br />而这两个数恰恰等于对方的真因子各自加��h��的和�Q�sum[i]表示数i 的各个真因子的和�Q�,�?br />220=1+2+4+71+142=sum[284],
284=1+2+4+5+10+11+20+22+44+55+110=sum[220]�?br />�?84的真因子之和sum[284]=220�Q�且220的真因子之和sum[220]=284�Q�即有sum[220]=sum[sum[284]]=284�?/p>
如此�Q�是否已看出丝毫端�?
如上所�C�,考虑�?是每个整数的因子�Q�把出去整数本��n之外的所有因子叫做这个数�?#8220;真因�?#8221;。如果两个整敎ͼ�其中每一个真因子的和都恰好等于另一个数�Q�那么这两个敎ͼ����构成一�?#8220;亲和�?#8221;�Q�有关亲和数的更多讨论,可参考这�Q?a title="http://en.wikipedia.org/wiki/Amicable_pair" target="_blank" style="color: #336699; text-decoration: initial;">http://t.cn/hesH09�Q��?/p>
求解�Q?/strong> �W�三节、程序的构造与解释 因�ؓ(f��)所有数的真因数都包�?�Q�所以,先在各个数的下方全部�|?
了解了什么是亲和敎ͼ�接下来咱们一步一步来解决上面提出的问题(以下内容大部引自水的原话�Q�同时水哥有一句原话,“在你真正弄弄懂这个范例之前,你不配说你懂数据�l�构和算�?/strong>”�Q��?/p>
�W�二节、伴随数�l�线性遍�?/span>
依据上文中的�W?�Ҏ(gu��)���\�Q�编写如下代码:(x��)
int main()
{
int i, j;
for (i = 0; i <= 5000000; i++)
sum[i] = 1; //1是所有数的真因数所以全部置1
for (i = 2; i + i <= 5000000; i++)
{
//5000000以下最大的真因数是不超�q�它的一半的
j = i + i; //因�ؓ(f��)真因敎ͼ�所以不能算本��n�Q�所以从它的2倍开�?nbsp;
while (j <= 5000000)
{
//���所有i的倍数的位�|�上加i
sum[j] += i;
j += i;
}
}
for (i = 220; i <= 5000000; i++) //扫描�Q�O�Q�N�Q��?nbsp;
{
// 一�ơ遍历,因�ؓ(f��)知道最���是220�?84因此�?20开�?nbsp;
if (sum[i] > i && sum[i] <= 5000000 && sum[sum[i]] == i)
{
//去重�Q�不���界�Q�满���亲�?nbsp;
printf("%d %d/n",i,sum[i]);
}
}
return 0;
}
我再来具体解释下上述�E�序的原理,ok�Q��D个例子,假设是求10以内的亲和数�Q�求解步骤如下:(x��)
1 2 3 4 5 6 7 8 9 10
1 1 1 1 1 1 1 1 1 1
2 2 2 2
3 3
4
5
���i对应的数下面的各个真因子加�v来得��C��个和sum[i]�Q�如果这个和sum[i]==某个i’�Q�且sum[i‘]=i�Q?br />那么�q�两个数i和i’�Q�即��Z��对亲和数�?/li>
i=3�Q�sum[6]+=3�Q�sum[9]+=3...
......
]]>
作者:(x��)July�Q�yansha�Q�zhouzhenren�?br /> 致谢�Q�微�?00题实现组�Q�编�E�艺术室�?br /> 微博�Q?a target="_blank" style="color: #336699; text-decoration: initial;">http://weibo.com/julyweibo �?br /> 出处�Q?a target="_blank" style="color: #336699; text-decoration: initial;">http://blog.csdn.net/v_JULY_v �?br /> wiki�Q?a target="_blank" style="color: #336699; text-decoration: initial;">http://tctop.wikispaces.com/�?br />------------------------------
前奏
希望此编�E�艺术系列能�l�各位带来的是一�U�方法,一�U�创造力�Q�一�U��D一反三的能力。本章依然同�W�四章一��P��选取比较���单的面试题,恭祝各位旅途愉快。同��P��有�Q何问题,�Ƣ迎不吝指正。谢谢�?/p>
分析�Q?/p> �׃��试着一步一步解册���个问题(注意阐述中数列有序无序的区别�Q�:(x��)
�W�一节、寻扑֒�为定值的两个�?/span>
�W?4题(数组�Q�:(x��)
题目�Q�输入一个数�l�和一个数字,在数�l�中查找两个敎ͼ�使得它们的和正好是输入的那个数字�?br />要求旉���复杂度是O(n)。如果有多对数字的和�{�于输入的数字,输出��L��一对即可�?br />例如输入数组1�?�?�?�?1�?5和数�?5。由�?+11=15�Q�因此输�?�?1�?/p>
�Q��?/li>
原始序列�Q?�?2�?4�?7�?1�?5 用输入数�?5减一下各个数�Q�得到对应的序列为:(x��)
对应序列�Q?4�?3�?1�?�?�?0
�W�一个数�l�以一指针i 从数�l�最左端开始向��x��描,�W�二个数�l�以一指针j 从数�l�最右端开始向左扫描,如果下面出现了和上面一��L(f��ng)��敎ͼ�即a[*i]=a[*j]�Q�就扑և��q�俩个数来了。如上,i�Q�j最�l�在�W�一个,和第二个序列中找��C��相同的数4�?1�Q�,所以符合条件的两个敎ͼ�即�ؓ(f��)4+11=15。怎么��P��两端同时查找�Q�时间复杂度瞬间�~�短��C��O�Q�N�Q�,但却同时需要O�Q�N�Q�的�I�间存储�W�二个数�l�(@飞羽�Q?span style="font-size: 12px;">要达到O(N)的复杂度�Q�第一个数�l�以一指针i 从数�l�最左端开始向��x��描,�W�二个数�l�以一指针j 从数�l�最右端开始向左扫描,首先初始i指向元素1�Q�j指向元素0�Q�谁指的元素���,谁先�U�d���Q�由�?�Q�i�Q?gt;0�Q�j�Q�,所以i不动�Q�j向左�U�d��。然后j�U�d��到元�?发现大于元素1�Q�故而停止移动j�Q�开始移动i�Q�直到i指向4�Q�这�?i指向的元素与j指向的元素相�{�,故而判�?是满���x��件的�W�一个数�Q�然后同时移动i,j再进行判断,直到它们到达边界
�ȝ���Q?/p>
- 不论原序列是有序�q�是无序�Q�解册����c�题有以下三�U�办法:(x��)1、二分(若无序,先排序后二分�Q�,旉���复杂度��Mؓ(f��)O�Q�n*logn�Q�,�I�间复杂度�ؓ(f��)O�Q?�Q�;2、扫描一遍X-S[i] 映射��C��个数�l�或构造hash表,旉���复杂度�ؓ(f��)O�Q�n�Q�,�I�间复杂度�ؓ(f��)O�Q�n�Q�;3、两个指针两端扫描(若无序,先排序后扫描�Q�,旉���复杂度最后�ؓ(f��)�Q�有序O�Q�n�Q�,无序O�Q�n*logn+n�Q?O�Q�n*logn�Q�,�I�间复杂度都为O�Q?�Q��?/li>
- 所以,要想辑ֈ�旉���O�Q�N�Q�,�I�间O�Q?�Q�的目标�Q�除非原数组是有序的�Q�指针扫描法�Q�,不然�Q�当数组无序的话�Q�就只能先排序,后指针扫描法或二分(旉���n*logn�Q�空间O�Q?�Q�)�Q�或映射或hash�Q�时间O�Q�n�Q�,�I�间O�Q�n�Q�)。时间或�I�间�Q�必��ȝ��牲一个,自个权衡吧�?/li>
- �l�g���Q�若是数�l?strong>有序的情况下�Q�优先考虑两个指针两端扫描法,以达到最佳的�Ӟ��O�Q�N�Q�)�Q�空�Q�O�Q?�Q�)效应。否则,如果要排序的话,旉���复杂度最快当然是只能辑ֈ�N*logN�Q�空间O�Q?�Q�则是不在话下�?/li>
代码�Q?/strong>
ok�Q�在�q�入�W�二节之前,�׃��先来实现思�\5�Q�这里假定数�l�已�l�是有序的)�Q�代码可以如下编写(两段代码实现�Q�:(x��)
- //代码一
- //O�Q�N�Q?/span>
- Pair findSum(int *s,int n,int x)
- {
- //sort(s,s+n); 如果数组非有序的�Q�那��׃��先排好序O�Q�N*logN�Q?nbsp;
- int *begin=s;
- int *end=s+n-1;
- while(begin<end) //俩头多w��|��或称两个指针两端扫描法,很经典的�Ҏ(gu��)���Q�O�Q�N�Q?nbsp;
- {
- if(*begin+*end>x)
- {
- --end;
- }
- else if(*begin+*end<x)
- {
- ++begin;
- }
- else
- {
- return Pair(*begin,*end);
- }
- }
- return Pair(-1,-1);
- }
- //或者如下编写,
- //代码�?/span>
- //copyright@ zhedahht && yansha
- //July、updated�Q?011.05.14�?/span>
- bool find_num(int data[], unsigned int length, int sum, int& first_num, int& second_num)
- {
- if(length < 1)
- return true;
- int begin = 0;
- int end = length - 1;
- while(end > begin)
- {
- long current_sum = data[begin] + data[end];
- if(current_sum == sum)
- {
- first_num = data[begin];
- second_num = data[end];
- return true;
- }
- else if(current_sum > sum)
- end--;
- else
- begin++;
- }
- return false;
- }
扩展�Q?/strong>
1、如果在�q�回扑ֈ�的两个数的同�Ӟ���q�要求你�q�回�q�两个数的位�|�列?
2、如果把题目中的要你��L��的两个数改�ؓ(f��)“多个�?#8221;�Q�或��L��个数�?�Q�请看下面第二节�Q?br />3、二分查找时�Q?left <= right�Q�right = middle - 1;left < right�Q�right = middle;
//���法所操作的区�?是左闭右开区间,�q�是左闭右闭区间,�q�个区间,需要在循环初始�?
//循环体是否终止的判断�?以及(qi��ng)每次修改left,right区间��D��三个地方保持一�?否则���可能出�?//二分查找实现一
int search(int array[], int n, int v)
{
int left, right, middle;
left = 0, right = n - 1;
while (left <= right)
{
middle = left + (right-left)/2;
if (array[middle] > v)
{
right = middle - 1;
}
else if (array[middle] < v)
{
left = middle + 1;
}
else
{
return middle;
}
}
return -1;
}//二分查找实现�?br />int search(int array[], int n, int v)
{
int left, right, middle;
left = 0, right = n;
while (left < right)
{
middle = left + (right-left)/2;
if (array[middle] > v)
{
right = middle;
}
else if (array[middle] < v)
{
left = middle + 1;
}
else
{
return middle;
}
}
return -1;
}
解法一 解法�?/strong> 代码�~�写如下�Q?/p> 扩展�Q?/strong> 1、从一列数中筛除尽可能���的��C��得从左往右看�Q�这些数是从���到大再从大到小的(�|�易�Q��?/p> 2、有两个序列a,b�Q�大���都为n,序列元素的��g�Q意整敎ͼ�无序�Q?br />要求�Q�通过交换a,b中的元素�Q���[序列a元素的和]与[序列b元素的和]之间的差最����?br />例如: @well�Q�[fairywell]: @yansha�Q�fairywell的程序很赞,旉���复杂度O(nlogn)�Q�这也是我能惛_��的时间复杂度最优��g��。不知能不能辑ֈ�O(n)�?/span> 扩展题第2�?/span> 当前数组a和数�l�b的和之差�?br /> A = sum(a) - sum(b) a的第i个元素和b的第j个元素交换后�Q�a和b的和之差�?br /> A' = sum(a) - a[i] + b[j] - �Q�sum(b) - b[j] + a[i]) 设x = a[i] - b[j]�Q�得 假设A > 0, 当x �?(0,A)之间�Ӟ��做这��L(f��ng)��交换才能使得交换后的a和b的和之差变小�Q�x���接�q�A/2效果���好, 所以算法大概如下:(x��) 接上�Q�@yuan�Q?br />a[i]-b[j]要接�q�A/2�Q�则可以�q�样惻I�� 查找最后一个小于等于a[k]-C的数和第一个大于等于a[k]-C的数�Q?br />然后看哪一个与a[k]-C更加接近�Q�所以T(n) = nlogn�?/span> 除此之外�Q�受本文读�?span style="color: #666666; font-family: Arial, Console, Verdana, 'Courier New'; line-height: 14px;">xiafei1987128启示�Q?/span>有朋友在stacoverflow上也问过一个类似的题,:-)�Q�见此:(x��)http://stackoverflow.com/questions/9047908/swap-the-elements-of-two-sequences-such-that-the-difference-of-the-element-sums。感兴趣的可以看看�?/span> 本章完�?/p> �E�序员面试题狂想�?tctop�Q�the crazy thinking of programers�Q�的修订wiki�Q?a target="_blank" style="color: #336699; text-decoration: initial;">http://tctop.wikispaces.com/�Q�已建立�Q�我们急切的想得到读者的反馈�Q�意见,������Q�以�?qi��ng)更好的思�\�Q�算法,和代码优化的�����。所以, •如果你发��C��狂想曲系列中的�Q何一题,��M��一章(http://t.cn/hgVPmH�Q�中的错误,问题�Q�与漏洞�Q�欢�q�告知给我们�Q�我们将感激不尽�Q�同�Ӟ��免费赠送本blog内的全部博文集锦的CHM文�g1期; 版权所有,本�h�Ҏ(gu��)��blog内所有�Q何内容��n有版权及(qi��ng)著作权。实要�{载,请以链接形式注明出处�?/strong>
�W�二节、寻扑֒�为定值的多个�?/span>
�W?1题(数组�Q?br />2010�q�中兴面试题
�~�程求解�Q?br />输入两个整数 n �?m�Q�从数列1�Q?�Q?.......n �?随意取几个数,
使其和等�?m ,要求���其中所有的可能�l�合列出来�?/p>
我想�Q�稍后给出的�E�序已经���_��清楚了,���是要注意到放n�Q�和不放n个区别,卛_���Q�代码如下:(x��)
@zhouzhenren�Q?br />�q�个问题属于子集和问题(也是背包问题�Q�。本�E�序采用 回溯�?剪枝
X数组是解向量�Q�t=∑(1,..,k-1)Wi*Xi, r=∑(k,..,n)Wi
若t+Wk+W(k+1)<=M,则Xk=true�Q�递归左儿�?X1,X2,..,X(k-1),1)�Q�否则剪枝;
若t+r-Wk>=M && t+W(k+1)<=M,则置Xk=0�Q�递归叛_���?X1,X2,..,X(k-1),0)�Q�否则剪枝;
本题中W数组���是(1,2,..,n),所以直接用k代替WK倹{�?/p>
var a=[100,99,98,1,2, 3];
var b=[1, 2, 3, 4,5,40];�Q?a target="_blank" style="color: #336699; text-decoration: initial;">微��Y100�?/span>�W?2题)�?/p>
�l�出扩展问题 1 的一个解法:(x��)
1、从一列数中筛除尽可能���的��C��得从左往右看�Q�这些数是从���到大再从大到小的(�|�易�Q��?br />双端 LIS 问题�Q�用 DP 的思想可解�Q�目标规划函�?max{ b[i] + c[i] - 1 }, 其中 b[i] ��Z��左到叻I�� 0 ~ i 个数之间满��递增的数字个敎ͼ� c[i] ��Z��叛_��左, n-1 ~ i 个数之间满��递增的数字个数。最后结果�ؓ(f��) n - max + 1。其�?DP 的时候,可以�l�护一�?inc[] 数组表示递增数字序列�Q�inc[i] ��Z�����到大第 i 大的数字�Q�然后在计算 b[i] c[i] 的时候��用二分查扑֜� inc[] 中找出区�?inc[0] ~ inc[i-1] 中小�?a[i] 的元素个敎ͼ�low�Q��?br />源代码如下:(x��)
= sum(a) - sum(b) - 2 (a[i] - b[j])
= A - 2 (a[i] - b[j])
|A| - |A'| = |A| - |A-2x|
如果找不到在(0,A)之间的x�Q�则当前的a和b���是�{�案�?/span>
在a和b中寻找��得x�?0,A)之间�q�且最接近A/2的i和j�Q�交换相应的i和j元素�Q�重新计���A后,重复前面的步骤直��x��不到(0,A)之间的x为止�?nbsp;
我们可以对于a数组的�Q意一个a[k],在数�l�b中找��Z��a[k]-C最接近的数�Q�C���是常数�Q�也���是0.5*A�Q?br />�q�个数要么就是a[k]-C�Q�要么就是比他稍大,要么比他�E�小�Q�所以可以要二分查找�?/span>
•如果你能对狂��x���p�d��的创作提供�Q何徏设性意见,或指��|���Ƣ迎反馈�l�我们,�q�真诚邀��h��加入到狂��x��的wiki修订工作中;
•如果你是�~�程高手�Q�对狂想曲的��M��一章有自己更好的思�\�Q�或���法�Q�欢�q�加入狂��x��的创作组�Q�以为千千万万的读者创造更多的价��|��更好的服务�?br />Ps�Q�狂��x��tctop的wiki修订地址为:(x��)http://tctop.wikispaces.com/。欢�q�围观,更欢�q��?zh��n)�加入到狂��x��的创作或wiki修订中�?/span>
]]>
]]>
]]>
]]>