еҚ•жәҗжңҖзҹӯиө\еҫ„й—®йўҳпјҢеҚӣ_ңЁеӣҫдёӯжұӮеҮәҫlҷе®ҡҷе¶зӮ№еҲ°е…¶е®ғд“QдёҖҷе¶зӮ№зҡ„жңҖзҹӯиө\еҫ„гҖӮеңЁеј„жё…жҘҡеҰӮдҪ•жұӮҪҺ—еҚ•жәҗжңҖзҹӯиө\еҫ„й—®йўҳд№ӢеүҚпјҢеҝ…йЎ»еј„жё…жҘҡжңҖзҹӯиө\еҫ„зҡ„жңҖдјҳеӯҗҫl“жһ„жҖ§иҙЁгҖ?/p>
дёҖ.жңҖзҹӯиө\еҫ„зҡ„жңҖдјҳеӯҗҫl“жһ„жҖ§иҙЁ
иҜҘжҖ§иҙЁжҸҸиҝ°дёәпјҡеҰӮжһңP(i,j)={Vi....Vk..Vs...Vj}жҳҜд»Һҷе¶зӮ№iеҲ°jзҡ„жңҖзҹӯиө\еҫ„пјҢkе’ҢsжҳҜиҝҷжқЎиө\еҫ„дёҠзҡ„дёҖдёӘдёӯй—ҙйЎ¶зӮ№пјҢйӮЈд№ҲP(k,s)еҝ…е®ҡжҳҜд»ҺkеҲ°sзҡ„жңҖзҹӯиө\еҫ„гҖӮдёӢйқўиҜҒжҳҺиҜҘжҖ§иҙЁзҡ„жӯЈјӢ®жҖ§гҖ?/p>
еҒҮи®ҫP(i,j)={Vi....Vk..Vs...Vj}жҳҜд»Һҷе¶зӮ№iеҲ°jзҡ„жңҖзҹӯиө\еҫ„пјҢеҲҷжңүP(i,j)=P(i,k)+P(k,s)+P(s,j)гҖӮиҖҢP(k,s)дёҚжҳҜд»ҺkеҲ°sзҡ„жңҖзҹӯи·қјӣ»пјҢйӮЈд№Ҳеҝ…е®ҡеӯҳеңЁеҸҰдёҖжқЎд»ҺkеҲ°sзҡ„жңҖзҹӯиө\еҫ„P'(k,s)еQҢйӮЈд№ҲP'(i,j)=P(i,k)+P'(k,s)+P(s,j)<P(i,j)гҖӮеҲҷдёҺP(i,j)жҳҜд»ҺiеҲ°jзҡ„жңҖзҹӯиө\еҫ„зӣёзҹӣзӣҫгҖӮеӣ жӯӨиҜҘжҖ§иҙЁеҫ—иҜҒгҖ?/p>
дә?DijkstraҪҺ—жі•
з”ЧғёҠҳq°жҖ§иҙЁеҸҜзҹҘеQҢеҰӮжһңеӯҳеңЁдёҖжқЎд»ҺiеҲ°jзҡ„жңҖзҹӯиө\еҫ?Vi.....Vk,Vj)еQҢVkжҳҜVjеүҚйқўзҡ„дёҖҷе¶зӮ№гҖӮйӮЈд№?Vi...Vk)д№ҹеҝ…е®ҡжҳҜд»ҺiеҲ°kзҡ„жңҖзҹӯиө\еҫ„гҖӮдШ“дәҶжұӮеҮәжңҖзҹӯиө\еҫ„пјҢDijkstraһ®ұжҸҗеҮЮZәҶд»ҘжңҖзҹӯиө\еҫ„й•ҝеәҰйҖ’еўһеQҢйҖҗж¬Ўз”ҹжҲҗжңҖзҹӯиө\еҫ„зҡ„ҪҺ—жі•гҖӮиӯ¬еҰӮеҜ№дәҺжәҗҷе¶зӮ№V0еQҢйҰ–е…ҲйҖүжӢ©е…¶зӣҙжҺҘзӣёйӮИқҡ„ҷе¶зӮ№дёӯй•ҝеәҰжңҖзҹӯзҡ„ҷе¶зӮ№ViеQҢйӮЈд№ҲеҪ“еүҚе·ІзҹҘеҸҜеҫ—д»ҺV0еҲ°иҫҫVjҷе¶зӮ№зҡ„жңҖзҹӯи·қјӣ»dist[j]=min{dist[j],dist[i]+matrix[i][j]}гҖӮж №жҚ®иҝҷҝUҚжҖқиө\еQ?/p>
еҒҮи®ҫеӯҳеңЁG=<V,E>еQҢжәҗҷе¶зӮ№дёәV0еQҢU={V0},dist[i]и®°еҪ•V0еҲ°iзҡ„жңҖзҹӯи·қјӣ»пјҢpath[i]и®°еҪ•д»ҺV0еҲ°iи·Ҝеҫ„дёҠзҡ„iеүҚйқўзҡ„дёҖдёӘйЎ¶зӮҸVҖ?/p>
1.д»ҺV-UдёӯйҖүжӢ©дҪҝdist[i]еҖјжңҖһ®Ҹзҡ„ҷе¶зӮ№iеQҢе°ҶiеҠ е…ҘеҲ°Uдёӯпјӣ
2.жӣҙж–°дёҺiзӣҙжҺҘзӣ”RӮ»ҷе¶зӮ№зҡ„distеҖ№{Җ?dist[j]=min{dist[j],dist[i]+matrix[i][j]})
3.зҹҘйҒ“U=VеQҢеҒңжӯўгҖ?/p>
д»Јз Ғе®һзҺ°:
#include <iostream>
#include<stack>
#define M 100
#define N 100
using namespace std;
typedef struct node
{
int matrix[N][M]; //йӮАLҺҘзҹ©йҳө
int n; //ҷе¶зӮ№ж•?nbsp;
int e; //иҫТҺ•°
}MGraph;
void DijkstraPath(MGraph g,int *dist,int *path,int v0) //v0иЎЁзӨәжәҗйЎ¶зӮ?nbsp;
{
int i,j,k;
bool *visited=(bool *)malloc(sizeof(bool)*g.n);
for(i=0;i<g.n;i++) //еҲқе§ӢеҢ?nbsp;
{
if(g.matrix[v0][i]>0&&i!=v0)
{
dist[i]=g.matrix[v0][i];
path[i]=v0; //pathи®°еҪ•жңҖзҹӯиө\еҫ„дёҠд»Һv0еҲ°iзҡ„еүҚдёҖдёӘйЎ¶зӮ?nbsp;
}
else
{
dist[i]=INT_MAX; //иӢҘiдёҚдёҺv0зӣҙжҺҘзӣ”RӮ»еQҢеҲҷжқғеҖјзҪ®дёәж— ҪI·еӨ§
path[i]=-1;
}
visited[i]=false;
path[v0]=v0;
dist[v0]=0;
}
visited[v0]=true;
for(i=1;i<g.n;i++) //еҫӘзҺҜжү©еұ•n-1ӢЖ?nbsp;
{
int min=INT_MAX;
int u;
for(j=0;j<g.n;j++) //еҜАLүҫжңӘиў«жү©еұ•зҡ„жқғеҖјжңҖһ®Ҹзҡ„ҷе¶зӮ№
{
if(visited[j]==false&&dist[j]<min)
{
min=dist[j];
u=j;
}
}
visited[u]=true;
for(k=0;k<g.n;k++) //жӣҙж–°distж•°з»„зҡ„еҖје’Ңи·Ҝеҫ„зҡ„еҖ?nbsp;
{
if(visited[k]==false&&g.matrix[u][k]>0&&min+g.matrix[u][k]<dist[k])
{
dist[k]=min+g.matrix[u][k];
path[k]=u;
}
}
}
}
void showPath(int *path,int v,int v0) //жү“еҚ°жңҖзҹӯиө\еҫ„дёҠзҡ„еҗ„дёӘйЎ¶зӮ?nbsp;
{
stack<int> s;
int u=v;
while(v!=v0)
{
s.push(v);
v=path[v];
}
s.push(v);
while(!s.empty())
{
cout<<s.top()<<" ";
s.pop();
}
}
int main(int argc, char *argv[])
{
int n,e; //иЎЁзӨәиҫ“е…Ҙзҡ„йЎ¶зӮТҺ•°е’Ңиҫ№ж•?nbsp;
while(cin>>n>>e&&e!=0)
{
int i,j;
int s,t,w; //иЎЁзӨәеӯҳеңЁдёҖжқЎиҫ№s->t,жқғеҖйgШ“w
MGraph g;
int v0;
int *dist=(int *)malloc(sizeof(int)*n);
int *path=(int *)malloc(sizeof(int)*n);
for(i=0;i<N;i++)
for(j=0;j<M;j++)
g.matrix[i][j]=0;
g.n=n;
g.e=e;
for(i=0;i<e;i++)
{
cin>>s>>t>>w;
g.matrix[s][t]=w;
}
cin>>v0; //иҫ“е…ҘжәҗйЎ¶зӮ?nbsp;
DijkstraPath(g,dist,path,v0);
for(i=0;i<n;i++)
{
if(i!=v0)
{
showPath(path,i,v0);
cout<<dist[i]<<endl;
}
}
}
return 0;
}
еӣӯеӯҗйҮҢжңүеҫҲеӨҡж·Юp—ҸдёҚжјҸзҡ„й«ҳжүӢпјҢеңЁиҝҷйҮҢиҒҠҳqҷз§Қеҹәжң¬й—®йўҳжҳҜжңүзӮ№е°Ҹе„ҝ科гҖӮдёҚҳqҮжң¬дәәеҸӘжҳҜжғіеҲҶднnдёӢиҮӘе·Юqҡ„ж–°зҡ„еQҢд»Јз ҒпјҢҪҺ—жі•жңүдёҚӯ‘ід№ӢеӨ„пјҢҳqҳиҜ·еӨ§е®¶жҢҮжӯЈеQҢе…ұеҗҢиҝӣжӯҘгҖ?/p>
ҳqҷз§Қйўҳд№ҹжҳҜдёҖйҒ“з»Ҹе…ёзҡ„йқўиҜ•йўҳпјҢдё»иҰҒиҖғеҜҹҳqӣеҲ¶иҪ¬жҚўҫlҶжғіеQҢCodingиҙЁйҮҸҪ{үгҖ?/p>
еҪ“жҲ‘们жҠҠеҚҒиҝӣеҲ¶иқ{жҲҗдәҢҳqӣеҲ¶зҡ„ж—¶еҖҷпјҢжҲ‘们йҖҡиҝҮиҫ—иқ{зӣ”RҷӨеQҢеҸ–дҪҷпјҢйҖҶзҪ®дҪҷж•°еәҸеҲ—зҡ„иҝҮҪEӢеҫ—еҲ°ж–°зҡ„иҝӣеҲ¶зҡ„ж•°гҖӮеӣ жӯӨжҲ‘们еҸҜд»ҘеҖҹеҠ©ҳqҷз§ҚжҖқжғіжҠҠMҳqӣеҲ¶иҪ¬жҲҗNҳqӣеҲ¶зҡ„ж•°гҖ?/p>
еҰӮдёӢжҳҜCзҡ„иҜҰҫlҶзҡ„е®һзҺ°ж–ТҺі•
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 |
void m2n(int m, char* mNum, int n, char* nNum) { int i = 0; char c, *p = nNum; //ҳqҷжҳҜдёҖдёӘиҖғеҜҹең°ж–№еQҢжҳҜеҗҰиғҪз”ЁжңҖһ®‘д№ҳжі•ж¬Ўж•°гҖ? while (*mNum != '\0') i = i*m + *mNum++ - '0'; //иҫ—иқ{еҸ–дҪҷ while (i) { *p++ = i % n + '0'; i /= n; } *p-- = '\0'; //йҖҶзҪ®дҪҷж•°еәҸеҲ— while (p > nNum) { c = *p; *p-- = *nNum; *nNum++ = c; } } |
и§ӮеҜҹдёҠйқўзҡ„д»Јз ҒпјҢеӯҳеңЁзқҖдј—еӨҡзҡ„дёҚӯ‘ҹлҖӮдҫӢеҰӮпјҢиҰҒеҜ№иҫ“е…ҘеҸӮж•°еҒҡжЈҖжҹҘпјҢж•°еҖјзҡ„еӨ§е°Ҹ收еҲ°intеҖјжңҖеӨ§еҖјзҡ„йҷҗеҲ¶Ҫ{үгҖӮдёҚҳqҮеҘҪеңЁдёҖзӮ№пјҢиҜҘз®—жі•зҡ„ж—үҷ—ҙеӨҚжқӮеәҰжҳҜO(n)зҡ„гҖ?/p>
жҲ‘们йңҡwӣіж— ж•Ңзҡ„иҷnеӨ§еҸ”еҸҲжҸҗдҫӣдәҶдёҖҝUҚз”ЁJavaе®һзҺ°зҡ„йҖҡз”Ёзҡ„иҝӣеҲ¶иқ{жҚўж–№жі•пјҢеҚідӢЙWindowsзҡ„и®ЎҪҺ—еҷЁд№ҹиқ{дёҚдәҶзҡ„еӨ§ж•ҺНјҢҳqҷдёӘҪҺ—жі•д№ҹеҸҜд»Ҙиқ{гҖӮз®—е’ҢдёҠйқўзҡ„ҪҺ—жі•зӣёжҜ”еQҢд»–зҡ„еҹәжң¬жҖқжғідёҚеҸҳеQҢиҝҳжҳҜиҫ—иҪ¬йҷӨеQҢдҪҶжҳҜз”ЁдәҶеӯ—ҪWҰдёІеҒҡеӨ§ж•°зӣёйҷӨпјҢеҫҲдёҚй”ҷзҡ„еҲӣж–°зӮ№пјҢиөһдёҖдёӘгҖӮд»Јз ҒеҰӮдёӢпјҡ
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69 |
package test; /** * еҠҹиғҪеQҡе°ҶдёҖдёӘж•°д»ҺMҳqӣеҲ¶иҪ¬жҚўжҲҗNҳqӣеҲ¶ * MValueеQҡMҳqӣеҲ¶ж•°зҡ„еӯ—з¬ҰдёІиЎЁҪCәж–№жі? * ShangеQҡдҝқеӯҳдёӯй—ҙиҝҗҪҺ—з»“жһ? * MеQҡMҳqӣеҲ¶ * NеQҡNҳqӣеҲ¶ */public class M2N { // еңЁиҝҷйҮҢеҜ№иҫ“е…ҘиөӢеҖ? public static String MValue = "1231412423534674574757"; public static String Shang = null; public static int M = 10; public static int N = 8; public static void main(String[] args) { String nValue = ""; Shang = MValue; while(Shang.length() > 0) { nValue = qiuyu(Shang) + nValue; } System.out.println(nValue); } /** * еҠҹиғҪеQҡеҜ№ҫlҷе®ҡзҡ„MҳqӣеҲ¶еӯ—з¬ҰдёІеҜ№nжұӮдҪҷгҖ? * * @param MTempValue * @param m * @param n * @return */ public static String qiuyu(String MTempValue) { Shang = ""; int temp = 0; while (MTempValue.length() > 0) { int t = getIntFromStr(MTempValue.substring(0, 1)); MTempValue = MTempValue.substring(1); temp = temp * M + t; Shang += getStrFromInt(temp / N); temp = temp % N; } while(Shang.length() > 0 && Shang.charAt(0) == '0'){ Shang = Shang.substring(1); } return getStrFromInt(temp); } public static int getIntFromStr(String str){ return str.charAt(0) <= '9' && str.charAt(0) >= '0'? str.charAt(0) - '0' : str.charAt(0) - 'a' + 10; } public static String getStrFromInt(int value){ String result = null; if(value>=0 && value<=9) result = String.valueOf((char)('0' + value)); else if(vlaue > 9 && value <36) { result = String.valueOf((char)('a' + value - 10)); } else { result = "-1";// еҮәй”ҷиҜҜдәҶ } return result; } } |
иөөеӨ§еҸ”зҡ„ҪҺ—жі•еҘҪдәҶдёҚе°‘еQҢйҷӨдәҶеҸӮж•°жЈҖжҹҘпјҢеӨ§е°ҸеҶҷд№ӢеӨ–йғҪеҫҲеҘҪгҖӮеҖјеҫ—жҲ‘们еҖҹйүҙгҖ?nbsp;

еҰӮдёҠеӣҫжүҖҪCәпјҢиҠӮзӮ№AеҲ°CжңүдёӨжқЎиө\еҫ„пјҢABCҳqҷжқЎи·Ҝеҫ„ҫlҸиҝҮдәҶдёҖдёӘиҠӮзӮ№пјҢиҖҢACи·Ҝеҫ„ҫlҸиҝҮдә?дёӘиҠӮзӮ№пјҢжҲ‘们зҡ„з®—жі•жүҖиҰҒеҒҡзҡ„дәӢһ®ұжҳҜиҰҒеңЁACи·Ҝеҫ„дёӯй—ҙеҠ е…ҘдёҖдёӘиҠӮзӮ№пјҢ然еҗҺABCи·Ҝеҫ„е’ҢADCи·Ҝеҫ„йғҪз»ҸҳqҮдәҶдёҖдёӘиҠӮзӮҸVҖ?br />
ҪҺ—жі•жҳҜиҝҷж пLҡ„еQҡеҜ№дәҺжҜҸдёӘиҠӮзӮ№з»ҙжҠӨдёҖҫl„дҝЎжҒҜпјҢеҢ…жӢ¬иҠӮзӮ№зҡ„еұӮж•ҺНјҲиө·е§ӢиҠӮзӮ№еҲ°иҜҘиҠӮзӮ№зҡ„иө\еҫ„й•ҝеәҰпјҢиө·е§ӢиҠӮзӮ№и®ҫдШ“0еQүд»ҘеҸҠз”ҹжҲҗиҜҘй•ҝеәҰзҡ„зҲ¶иҠӮзӮ№еQҢзӣёеҜ№дәҺеҸӣ_ӣҫеQҢиҠӮзӮ?ҫlҙжҠӨзҡ„дёҚҫlҸеӨ„зҗҶзҡ„дҝЎжҒҜһ®ұжҳҜеQҡеұӮж•?жқҘиҮӘиҠӮзӮ№3е’ҢиҠӮзӮ?еQӣиҠӮзӮ?ҫlҙжҠӨзҡ„дёҚҫlҸеӨ„зҗҶзҡ„дҝЎжҒҜһ®ұжҳҜеQҡеұӮж•?жқҘиҮӘиҠӮзӮ№5е’ҢиҠӮзӮ?д»ҘеҸҠеұӮж•°2жқҘиҮӘиҠӮзӮ№4еQӣиҠӮзӮ?зҡ„дёҚҫlҸеӨ„зҗҶзҡ„дҝЎжҒҜжҳҜпјҡеұӮж•°4жқҘиҮӘиҠӮзӮ№7еQҢеұӮж•?жқҘиҮӘиҠӮзӮ№7еQҢеұӮж•?жқҘиҮӘиҠӮзӮ№4гҖӮжҲ‘们算法жүҖиҰҒеҒҡзҡ„дәӢһ®ұжҳҜжңҖҫlҲдӢЙжҜҸдёӘиҠӮзӮ№йңҖиҰҒз»ҙжҠӨзҡ„еұӮдҝЎжҒҜеҸҳдёЮZёҖдёӘпјҢеҚПx— и®ЮZ»ҺйӮЈжқЎи·Ҝеҫ„еҲ°иҜҘиҠӮзӮ№еQҢиҜҘиҠӮзӮ№жүҖеӨ„зҡ„еұӮж•°йғҪжҳҜеӣәе®ҡзҡ„гҖӮз®—жі•еҰӮдёӢпјҡ
1гҖҒеҲқе§ӢеҢ–иө·е§ӢиҠӮзӮ№зҡ„еұӮж•оCҝЎжҒ?/span>
2гҖҒд»Һиө·е§ӢиҠӮзӮ№ејҖе§ӢйҒҚеҺҶжҜҸжқЎиө\еҫ„пјҢйҒҮеҲ°жҜҸдёӘиҠӮзӮ№з”ҹжҲҗдёҖдёӘз»ҙжҠӨдҝЎжҒ?/span>
еQ?еQүеҰӮжһңжӯӨиҠӮзӮ№дёҚеӯҳеңЁз»ҙжҠӨдҝЎжҒҜпјҢеҲӣеҫҸд№Ӣпјӣ
еQ?еQүеҰӮжһңиҜҘиҠӮзӮ№еӯҳеңЁҫlҙжҠӨдҝЎжҒҜеQҢжңүдёӨз§Қжғ…еҶөеQ?/span>
еQҲaеQүеҰӮжһңз”ҹжҲҗзҡ„ҫlҙжҠӨдҝЎжҒҜзҡ„еұӮж•°е’ҢеҺҹжқҘе·Іжңүзҡ„з»ҙжҠӨдҝЎжҒҜзҡ„еұӮж•°жҳҜзӣёеҗҢзҡ„еQҢеҲҷеҗҲеЖҲҳqҷдёӨдёӘз»ҙжҠӨдҝЎжҒҜпјҢжҜ”еҰӮеҜ№дәҺдҫӢеӯҗдёӯзҡ„еӣҫпјҢиҠӮзӮ№5еҺҹжқҘзҡ„з»ҙжҠӨдҝЎжҒҜдШ““еұӮж•°3жқҘиҮӘиҠӮзӮ№2”еQҢ然еҗҺд»ҺиҠӮзӮ№3еҲ°иҠӮзӮ?з”ҹжҲҗзҡ„з»ҙжҠӨдҝЎжҒҜдШ““еұӮж•°3жқҘиҮӘиҠӮзӮ№3”еQҢз”ұдәҺеұӮж•°зӣёеҗҢпјҢжҲ‘们еҸҜд»Ҙһ®Ҷе…¶еҗҲеЖҲдё?#8220;еұӮж•°3жқҘиҮӘиҠӮзӮ№2е’ҢиҠӮзӮ?”еQ?/span>
еQҲbеQүеҰӮжһңз”ҹжҲҗзҡ„ҫlҙжҠӨдҝЎжҒҜзҡ„еұӮж•°е’ҢеҺҹжқҘиҠӮзӮ№зҡ„з»ҙжҠӨдҝЎжҒҜзҡ„еұӮж•°дёҚдёҖиҮЯ_јҢжҲ‘们йңҖиҰҒжҜ”иҫғйӮЈдёҖдёӘзҡ„еұӮж•°иҫғеӨ§еQ?/span>
a.еҰӮжһңеҺҹжқҘҫlҙжҠӨдҝЎжҒҜзҡ„еұӮж•°иҫғеӨ§пјҢжӯӨж—¶еQҢжҲ‘们еҸӘйңҖиҰҒеңЁз”ҹжҲҗжӯӨз»ҙжҠӨдҝЎжҒҜзҡ„иҠӮзӮ№дёҺжӯӨиҠӮзӮ№д№Ӣй—ҙжҸ’е…ҘдёҖдёӘж–°зҡ„иҠӮзӮ№пјҢ然еҗҺз”ҹжҲҗж–°иҠӮзӮ№зҡ„ҫlҙжҠӨдҝЎжҒҜеQҢ然еҗҺд»Һж–°иҠӮзӮ№ејҖе§ӢпјҲ2еQүиҝҮҪE?/span>
b.еҰӮжһңж–°з”ҹжҲҗзҡ„ҫlҙжҠӨдҝЎжҒҜзҡ„еұӮж•°иҫғеӨ§пјҢһ®Ҷж–°з”ҹжҲҗзҡ„иҠӮзӮ№дҝЎжҒҜеӯҳе…ҘжӯӨиҠӮзӮ№еQҢ然еҗҺжҲ‘们йңҖиҰҒеңЁз”ҹжҲҗеҺҹжқҘҫlҙжҠӨдҝЎжҒҜзҡ„жүҖжңүиҠӮзӮ№е’ҢжӯӨиҠӮзӮ№д№Ӣй—ҙжҸ’е…Ҙж–°иҠӮзӮ№еQҢеЖҲдё”йңҖиҰҒд»ҺжүҖжңүзҡ„ж–°жҸ’е…ҘиҠӮзӮ№ејҖе§ӢпјҲ2еQүиҝҮҪE?br />
жңҖй•үKҖ’еўһеӯҗеәҸеҲ—й—®йўҳпјҡеңЁдёҖеҲ—ж•°дёӯеҜ»жүҫдёҖдәӣж•°еQҢиҝҷдәӣж•°ж»ЎиғцеQҡд“Qж„ҸдёӨдёӘж•°a[i]е’Ңa[j]еQҢиӢҘi<jеQҢеҝ…жңүa[i]<a[j]еQҢиҝҷж дhңҖй•ҝзҡ„еӯҗеәҸеҲ—з§°дёәжңҖй•үKҖ’еўһеӯҗеәҸеҲ—гҖ?/span>
и®ҫdp[i]иЎЁзӨәд»Ҙiдёәз»“һ®„Ўҡ„жңҖй•үKҖ’еўһеӯҗеәҸеҲ—зҡ„й•ҝеәҰеQҢеҲҷзҠ¶жҖҒиқ{ҝUАL–№ҪEӢдШ“еQ?/span>
dp[i] = max{dp[j]+1}, 1<=j<i,a[j]<a[i].
ҳqҷж ·ҪҺҖеҚ•зҡ„еӨҚжқӮеәҰдШ“O(n^2)еQҢе…¶е®һиҝҳжңүжӣҙеҘҪзҡ„ж–ТҺі•гҖ?/span>
иҖғиҷ‘дёӨдёӘж•°a[x]е’Ңa[y]еQҢx<yдё”a[x]<a[y],дё”dp[x]=dp[y]еQҢеҪ“a[t]иҰҒйҖүжӢ©ж—УһјҢеҲ°еә•еҸ–е“ӘдёҖдёӘжһ„жҲҗжңҖдјҳзҡ„е‘ўпјҹжҳ„Ў„¶йҖүеҸ–a[x]жӣҙжңүжҪңеҠӣеQҢеӣ дёәеҸҜиғҪеӯҳеңЁa[x]<a[z]<a[y]еQҢиҝҷж ·a[t]еҸҜд»ҘиҺ·еҫ—жӣҙдјҳзҡ„еҖ№{ҖӮеңЁҳqҷйҮҢҫlҷжҲ‘们дёҖдёӘеҗҜҪCәпјҢеҪ“dp[t]дёҖж дh—¶еQҢе°ҪйҮҸйҖүжӢ©жӣҙе°Ҹзҡ„a[x].
жҢүdp[t]=kжқҘеҲҶҫc»пјҢеҸӘйңҖдҝқз•ҷdp[t]=kзҡ„жүҖжңүa[t]дёӯзҡ„жңҖһ®ҸеҖы|јҢи®ҫd[k]и®°еҪ•ҳqҷдёӘеҖы|јҢd[k]=min{a[t],dp[t]=k}гҖ?/span>
ҳqҷж—¶жіЁж„ҸеҲ°dзҡ„дёӨдёӘзү№зӮ№пјҲйҮҚиҰҒеQүпјҡ
1. d[k]еңЁи®ЎҪҺ—иҝҮҪEӢдёӯеҚ•и°ғдёҚеҚҮеQ?nbsp;
2. dж•°з»„жҳҜжңүеәҸзҡ„еQҢd[1]<d[2]<..d[n]гҖ?/span>
еҲ©з”ЁҳqҷдёӨдёӘжҖ§иҙЁеQҢеҸҜд»ҘеҫҲж–№дҫҝзҡ„жұӮи§Јпјҡ
1. и®‘ЦҪ“еүҚе·ІжұӮеҮәзҡ„жңҖй•ҝдёҠеҚҮеӯҗеәҸеҲ—зҡ„й•ҝеәҰдШ“lenеQҲеҲқе§Ӣж—¶дё?еQүпјҢжҜҸж¬ЎиҜХd…ҘдёҖдёӘж–°е…ғзҙ xеQ?/span>
2. иӢҘx>d[len]еQҢеҲҷзӣҙжҺҘеҠ е…ҘеҲ°dзҡ„жң«һ®ҫпјҢдё”len++еQӣпјҲеҲ©з”ЁжҖ§иҙЁ2еQ?/span>
еҗҰеҲҷеQҢеңЁdдёӯдәҢеҲҶжҹҘжүҫпјҢжү‘ЦҲ°ҪW¬дёҖдёӘжҜ”xһ®Ҹзҡ„ж•°d[k]еQҢеЖҲd[k+1]=xеQҢеңЁҳqҷйҮҢx<=d[k+1]дёҖе®ҡжҲҗз«ӢпјҲжҖ§иҙЁ1,2еQүгҖ?/span>
- /**
- жңҖй•үKҖ’еўһеӯҗеәҸеҲ—O(nlogn)ҪҺ—жі•еQ?/span>
- зҠ¶жҖҒиқ{ҝUАL–№ҪEӢпјҡf[i] = max{f[i],f[j]+1},1<=j<i,a[j]<a[i].
- еҲҶжһҗеQҡеҠ е…Ҙx<y,f[x]>=f[y],еҲҷxзӣёеҜ№дәҺyжӣҙжңүжҪңеҠӣгҖ?/span>
- йҰ–е…Ҳж ТҺҚ®f[]еҖјеҲҶҫc»пјҢи®°еҪ•ж»Ўиғцf[t]=kзҡ„жңҖһ®Ҹзҡ„еҖјa[t],и®°d[k]=min{a[t]},f[t]=k.
- 1.еҸ‘зҺ°d[k]еңЁи®ЎҪҺ—иҝҮҪEӢдёӯеҚ•и°ғдёҚдёҠеҚ?/span>
- 2.d[1]<d[2]<...<d[k] (еҸҚиҜҒ) 1 2 3 8 4 7
- и§Јжі•еQ?/span>
- 1. и®‘ЦҪ“еүҚжңҖй•үKҖ’еўһеӯҗеәҸеҲ—дШ“len,иҖғиҷ‘е…ғзҙ a[i];
- 2. иӢҘd[len]<a[i],еҲҷlen++еQҢеЖҲһ®Ҷd[len]=a[i];
- еҗҰеҲҷ,еңЁd[0-len]дёӯдәҢеҲҶжҹҘжү?жү‘ЦҲ°ҪW¬дёҖдёӘжҜ”е®ғе°Ҹзҡ„е…ғзҙ d[k],тq¶d[k+1]=a[i].()
- */
- #include <iostream>
- #include <cstdio>
- #include <cstring>
- using namespace std;
- const int N = 41000;
- int a[N]; //a[i] еҺҹе§Ӣж•°жҚ®
- int d[N]; //d[i] й•ҝеәҰдёәiзҡ„йҖ’еўһеӯҗеәҸеҲ—зҡ„жңҖһ®ҸеҖ?/span>
- int BinSearch(int key, int* d, int low, int high)
- {
- while(low<=high)
- {
- int mid = (low+high)>>1;
- if(key>d[mid] && key<=d[mid+1])
- return mid;
- else if(key>d[mid])
- low = mid+1;
- else
- high = mid-1;
- }
- return 0;
- }
- int LIS(int* a, int n, int* d)
- {
- int i,j;
- d[1] = a[1];
- int len = 1; //йҖ’еўһеӯҗеәҸеҲ—й•ҝеә?/span>
- for(i = 2; i <= n; i++)
- {
- if(d[len]<a[i])
- j = ++len;
- else
- j = BinSearch(a[i],d,1,len) + 1;
- d[j] = a[i];
- }
- return len;
- }
- int main()
- {
- int t;
- int p;
- scanf("%d",&t);
- while(t--)
- {
- scanf("%d",&p);
- for(int i = 1; i <= p; i++)
- scanf("%d",&a[i]);
- printf("%d\n",LIS(a,p,d));
- }
- return 0;
- }
OJдёҠзҡ„дёҖдәӣж°ҙйў?еҸҜз”ЁжқҘз»ғжүӢе’ҢеўһеҠ иҮӘдҝЎ)
(poj3299,poj2159,poj2739,poj1083,poj2262,poj1503,poj3006,poj2255,poj3094)
еҲқжңҹ:
дёҖ.еҹәжң¬ҪҺ—жі•:
(1)жһҡдӢD. (poj1753,poj2965)
(2)иҙӘеҝғ(poj1328,poj2109,poj2586)
(3)йҖ’еҪ’е’ҢеҲҶжІАLі•.
(4)йҖ’жҺЁ.
(5)жһ„йҖ жі•.(poj3295)
(6)жЁЎжӢҹжі?(poj1068,poj2632,poj1573,poj2993,poj2996)
дә?еӣ„Ў®—жі?
(1)еӣ„Ўҡ„ж·ұеәҰдјҳе…ҲйҒҚеҺҶе’Ңе№ҝеәҰдјҳе…ҲйҒҚеҺ?
(2)жңҖзҹӯиө\еҫ„з®—жі?dijkstra,bellman-ford,floyd,heap+dijkstra)
(poj1860,poj3259,poj1062,poj2253,poj1125,poj2240)
(3)жңҖһ®Ҹз”ҹжҲҗж ‘ҪҺ—жі•(prim,kruskal)
(poj1789,poj2485,poj1258,poj3026)
(4)жӢ“жү‘жҺ’еәҸ (poj1094)
(5)дәҢеҲҶеӣ„Ўҡ„жңҖеӨ§еҢ№й…?(еҢҲзүҷеҲ©з®—жі? (poj3041,poj3020)
(6)жңҖеӨ§жөҒзҡ„еўһтqҝиө\ҪҺ—жі•(KMҪҺ—жі•). (poj1459,poj3436)
дё?ж•°жҚ®ҫl“жһ„.
(1)дё?(poj1035,poj3080,poj1936)
(2)жҺ’еәҸ(еҝ«жҺ’гҖҒеҪ’тq¶жҺ’(дёҺйҖҶеәҸж•°жңүе…?гҖҒе ҶжҺ? (poj2388,poj2299)
(3)ҪҺҖеҚ•еЖҲжҹҘйӣҶзҡ„еә”з”?
(4)е“ҲеёҢиЎЁе’ҢдәҢеҲҶжҹҘжүҫҪ{үй«ҳж•ҲжҹҘжүҫжі•(ж•°зҡ„Hash,дёІзҡ„Hash)
(poj3349,poj3274,POJ2151,poj1840,poj2002,poj2503)
(5)е“ҲеӨ«жӣјж ‘(poj3253)
(6)е ?nbsp;
(7)trieж ?йқҷжҖҒеҫҸж ‘гҖҒеҠЁжҖҒеҫҸж ? (poj2513)
еӣ?ҪҺҖеҚ•жҗңзҙ?nbsp;
(1)ж·ұеәҰдјҳе…ҲжҗңзғҰ (poj2488,poj3083,poj3009,poj1321,poj2251)
(2)тqҝеәҰдјҳе…ҲжҗңзғҰ(poj3278,poj1426,poj3126,poj3087.poj3414)
(3)ҪҺҖеҚ•жҗңзҙўжҠҖе·§е’ҢеүӘжһқ(poj2531,poj1416,poj2676,1129)
дә?еҠЁжҖҒ规еҲ?nbsp;
(1)иғҢеҢ…й—®йўҳ. (poj1837,poj1276)
(2)еһӢеҰӮдёӢиЎЁзҡ„з®ҖеҚ•DP(еҸҜеҸӮиҖғlrjзҡ„д№Ұ page149):
1.E[j]=opt{D+w(i,j)} (poj3267,poj1836,poj1260,poj2533)
2.E[i,j]=opt{D[i-1,j]+xi,D[i,j-1]+yj,D[i-1][j-1]+zij} (жңҖй•ҝе…¬е…ұеӯҗеәҸеҲ—)
(poj3176,poj1080,poj1159)
3.C[i,j]=w[i,j]+opt{C[i,k-1]+C[k,j]}.(жңҖдјҳдәҢеҲҶжЈҖзҙўж ‘й—®йўҳ)
е…?ж•°еӯҰ
(1)ҫl„еҗҲж•°еӯҰ:
1.еҠ жі•еҺҹзҗҶе’Ңд№ҳжі•еҺҹзҗ?
2.жҺ’еҲ—ҫl„еҗҲ.
3.йҖ’жҺЁе…ізі».
(POJ3252,poj1850,poj1019,poj1942)
(2)ж•°и®ә.
1.зҙ ж•°дёҺж•ҙйҷӨй—®йў?nbsp;
2.ҳqӣеҲ¶дҪ?
3.еҗҢдҪҷжЁЎиҝҗҪҺ?
(poj2635, poj3292,poj1845,poj2115)
(3)и®Ўз®—ж–ТҺі•.
1.дәҢеҲҶжі•жұӮи§ЈеҚ•и°ғеҮҪж•°зӣёе…ізҹҘиҜ?(poj3273,poj3258,poj1905,poj3122)
дё?и®Ўз®—еҮ дҪ•еӯ?
(1)еҮ дҪ•е…¬ејҸ.
(2)еҸүз§Ҝе’ҢзӮ№ҝUҜзҡ„ҳqҗз”Ё(еҰӮзәҝҢDлҠӣёдәӨзҡ„еҲӨе®ҡ,зӮ№еҲ°ҫUҝж®өзҡ„и·қјӣИқӯү). (poj2031,poj1039)
(3)еӨҡиҫ№еһӢзҡ„ҪҺҖеҚ•з®—жі?жұӮйқўҝU?е’Ңзӣёе…ӣ_ҲӨе®?зӮ№еңЁеӨҡиҫ№еһӢеҶ…,еӨҡиҫ№еһӢжҳҜеҗҰзӣёдә?
(poj1408,poj1584)
(4)еҮёеҢ…. (poj2187,poj1113)
дёӯзс”:
дёҖ.еҹәжң¬ҪҺ—жі•:
(1)C++зҡ„ж ҮеҮҶжЁЎзүҲеә“зҡ„еә”з”? (poj3096,poj3007)
(2)иҫғдШ“еӨҚжқӮзҡ„жЁЎжӢҹйўҳзҡ„и®ӯҫl?poj3393,poj1472,poj3371,poj1027,poj2706)
дә?еӣ„Ў®—жі?
(1)е·®еҲҶҫUҰжқҹҫpИқ»ҹзҡ„еҫҸз«Ӣе’ҢжұӮи§Ј. (poj1201,poj2983)
(2)жңҖһ®Ҹиҙ№з”ЁжңҖеӨ§жөҒ(poj2516,poj2195)
(3)еҸҢиҝһйҖҡеҲҶйҮ?poj2942)
(4)ејшҷҝһйҖҡеҲҶж”ҜеҸҠе…¶зҫғзӮ?(poj2186)
(5)еӣ„Ўҡ„еүІиҫ№е’ҢеүІзӮ?poj3352)
(6)жңҖһ®ҸеүІжЁЎеһӢгҖҒзҪ‘ҫlңжөҒ规зәҰ(poj3308, )
дё?ж•°жҚ®ҫl“жһ„.
(1)ҫUҝж®өж ? (poj2528,poj2828,poj2777,poj2886,poj2750)
(2)йқҷжҖҒдәҢеҸүжЈҖзҙўж ‘. (poj2482,poj2352)
(3)ж ‘зҠ¶ж ‘з»„(poj1195,poj3321)
(4)RMQ. (poj3264,poj3368)
(5)тq¶жҹҘйӣҶзҡ„й«ҳзс”еә”з”Ё. (poj1703,2492)
(6)KMPҪҺ—жі•. (poj1961,poj2406)
еӣ?жҗңзғҰ
(1)жңҖдјҳеҢ–еүӘжһқе’ҢеҸҜиЎҢжҖ§еүӘжһ?nbsp;
(2)жҗңзғҰзҡ„жҠҖе·§е’ҢдјҳеҢ– (poj3411,poj1724)
(3)и®°еҝҶеҢ–жҗңзҙ?poj3373,poj1691)
дә?еҠЁжҖҒ规еҲ?nbsp;
(1)иҫғдШ“еӨҚжқӮзҡ„еҠЁжҖҒ规еҲ?еҰӮеҠЁжҖҒ规еҲ’и§Јзү№еҲ«зҡ„ж–ҪиЎҢе•Ҷй—®йўҳҪ{?
(poj1191,poj1054,poj3280,poj2029,poj2948,poj1925,poj3034)
(2)и®°еҪ•зҠ¶жҖҒзҡ„еҠЁжҖҒ规еҲ? (POJ3254,poj2411,poj1185)
(3)ж ‘еһӢеҠЁжҖҒ规еҲ?poj2057,poj1947,poj2486,poj3140)
е…?ж•°еӯҰ
(1)ҫl„еҗҲж•°еӯҰ:
1.е®ТҺ–ҘеҺҹзҗҶ.
2.жҠҪеұүеҺҹзҗҶ.
3.ҫ|®жҚўҫҹӨдёҺPolyaе®ҡзҗҶ(poj1286,poj2409,poj3270,poj1026).
4.йҖ’жҺЁе…ізі»е’ҢжҜҚеҮҪж•°.
(2)ж•°еӯҰ.
1.й«ҳж–Ҝж¶Ҳе…ғжі?poj2947,poj1487, poj2065,poj1166,poj1222)
2.жҰӮзҺҮй—®йўҳ. (poj3071,poj3440)
3.GCDгҖҒжү©еұ•зҡ„ӢЖ§еҮ йҮҢеҜd(дёӯеӣҪеү©дҪҷе®ҡзҗҶ) (poj3101)
(3)и®Ўз®—ж–ТҺі•.
1.0/1еҲҶ数规еҲ’. (poj2976)
2.дёүеҲҶжі•жұӮи§ЈеҚ•еі?еҚ•и°·)зҡ„жһҒеҖ?
3.зҹ©йҳөжі?poj3150,poj3422,poj3070)
4.ҳqӯд»ЈйҖЖDҝ‘(poj3301)
(4)йҡҸжңәеҢ–з®—жі?poj3318,poj2454)
(5)жқӮйўҳ.
(poj1870,poj3296,poj3286,poj1095)
дё?и®Ўз®—еҮ дҪ•еӯ?
(1)еқҗж ҮјӣАL•ЈеҢ?
(2)жү«жҸҸҫUҝз®—жі?дҫӢеҰӮжұӮзҹ©еҪўзҡ„йқўз§Ҝе’Ңе‘Ёй•ҝеЖҲ,еёёе’ҢҫUҝж®өж ‘жҲ–е ҶдёҖиө·дӢЙз”?.
(poj1765,poj1177,poj1151,poj3277,poj2280,poj3004)
(3)еӨҡиҫ№еҪўзҡ„еҶ…ж ё(еҚҠег^йқўдәӨ)(poj3130,poj3335)
(4)еҮ дҪ•е·Ҙе…·зҡ„з»јеҗҲеә”з”?(poj1819,poj1066,poj2043,poj3227,poj2165,poj3429
)
й«ҳзс”:
дёҖ.еҹәжң¬ҪҺ—жі•иҰҒжұӮ:
(1)д»Јз Ғеҝ«йҖҹеҶҷжҲ?ҫ_„Ў®ҖдҪҶдёҚеӨұйЈҺж ?nbsp;
(poj2525,poj1684,poj1421,poj1048,poj2050,poj3306)
(2)дҝқиҜҒжӯЈзЎ®жҖ§е’Ңй«ҳж•ҲжҖ? poj3434
дә?еӣ„Ў®—жі?
(1)еәҰйҷҗеҲ¶жңҖһ®Ҹз”ҹжҲҗж ‘е’Ң第KжңҖзҹӯиө\. (poj1639)
(2)жңҖзҹӯиө\,жңҖһ®Ҹз”ҹжҲҗж ‘,дәҢеҲҶеӣ?жңҖеӨ§жөҒй—®йўҳзҡ„зӣёе…ізҗҶи®?дё»иҰҒжҳҜжЁЎеһӢеҫҸз«Ӣе’ҢжұӮи§Ј)
(poj3155, poj2112,poj1966,poj3281,poj1087,poj2289,poj3216,poj2446
(3)жңҖдјҳжҜ”зҺҮз”ҹжҲҗж ‘. (poj2728)
(4)жңҖһ®Ҹж ‘еҪўеӣҫ(poj3164)
(5)ӢЖЎе°Ҹз”ҹжҲҗж ?
(6)ж— еҗ‘еӣҫгҖҒжңүеҗ‘еӣҫзҡ„жңҖһ®ҸзҺҜ
дё?ж•°жҚ®ҫl“жһ„.
(1)trieеӣ„Ўҡ„е»әз«Ӣе’Ңеә”з”? (poj2778)
(2)LCAе’ҢRMQй—®йўҳ(LCA(жңҖҳq‘е…¬е…ЮqҘ–е…Ҳй—®йў? жңүзҰ»ҫUҝз®—жі?тq¶жҹҘйӣ?dfs) е’?еңЁзәҝҪҺ—жі•
(RMQ+dfs)).(poj1330)
(3)еҸҢз«ҜйҳҹеҲ—е’Ңе®ғзҡ„еә”з”?ҫlҙжҠӨдёҖдёӘеҚ•и°ғзҡ„йҳҹеҲ—,еёёеёёеңЁеҠЁжҖҒ规еҲ’дёӯиө·еҲ°дјҳеҢ–зҠ¶жҖҒиқ{ҝU?br />зҡ?nbsp;
зӣ®зҡ„). (poj2823)
(4)е·ҰеҒҸж ?еҸҜеҗҲтq¶е Ҷ).
(5)еҗҺзјҖж ?йқһеёёжңүз”Ёзҡ„ж•°жҚ®з»“жһ?д№ҹжҳҜиөӣеҢәиҖғйўҳзҡ„зғӯзӮ?.
(poj3415,poj3294)
еӣ?жҗңзғҰ
(1)иҫғйә»зғҰзҡ„жҗңзғҰйўҳзӣ®и®ӯз»ғ(poj1069,poj3322,poj1475,poj1924,poj2049,poj3426)
(2)тqҝжҗңзҡ„зҠ¶жҖҒдјҳеҢ?еҲ©з”ЁMҳqӣеҲ¶ж•°еӯҳеӮЁзҠ¶жҖҒгҖҒиқ{еҢ–дШ“дёІз”ЁhashиЎЁеҲӨйҮҚгҖҒжҢүдҪҚеҺӢҫ~©еӯҳеӮ?br />зҠ¶жҖҒгҖҒеҸҢеҗ‘е№ҝжҗңгҖҒA*ҪҺ—жі•. (poj1768,poj1184,poj1872,poj1324,poj2046,poj1482)
(3)ж·ұжҗңзҡ„дјҳеҢ?һ®ҪйҮҸз”ЁдҪҚҳqҗз®—гҖҒдёҖе®ҡиҰҒеҠ еүӘжһқгҖҒеҮҪж•°еҸӮж•°е°ҪеҸҜиғҪһ®‘гҖҒеұӮж•оCёҚжҳ“иҝҮеӨ?br />гҖҒеҸҜд»ҘиҖғиҷ‘еҸҢеҗ‘жҗңзғҰжҲ–иҖ…жҳҜиҪ®жҚўжҗңзғҰгҖҒIDA*ҪҺ—жі•. (poj3131,poj2870,poj2286)
дә?еҠЁжҖҒ规еҲ?nbsp;
(1)йңҖиҰҒз”Ёж•°жҚ®ҫl“жһ„дјҳеҢ–зҡ„еҠЁжҖҒ规еҲ?
(poj2754,poj3378,poj3017)
(2)еӣӣиҫ№еҪўдёҚҪ{үејҸзҗҶи®ә.
(3)иҫғйҡҫзҡ„зҠ¶жҖҒDP(poj3133)
е…?ж•°еӯҰ
(1)ҫl„еҗҲж•°еӯҰ.
1.MoBiusеҸҚжј”(poj2888,poj2154)
2.еҒҸеәҸе…ізі»зҗҶи®ә.
(2)еҚҡеҘ•и®?
1.жһҒеӨ§жһҒе°ҸҳqҮзЁӢ(poj3317,poj1085)
2.Nimй—®йўҳ.
дё?и®Ўз®—еҮ дҪ•еӯ?
(1)еҚҠег^йқўжұӮдә?poj3384,poj2540)
(2)еҸҜи§Ҷеӣ„Ўҡ„е»әз«Ӣ(poj2966)
(3)зӮҡwӣҶжңҖһ®ҸеңҶиҰҶзӣ–.
(4)еҜ№иёөзӮ?poj2079)
е…?ҫlјеҗҲйў?
(poj3109,poj1478,poj1462,poj2729,poj2048,poj3336,poj3315,poj2148,poj1263
)
ҪW¬еҚҒе…ӯз« гҖҒе…ЁжҺ’еҲ—й—®йўҳ
53.еӯ—з¬ҰдёІзҡ„жҺ’еҲ—гҖ?br />йўҳзӣ®еQҡиҫ“е…ҘдёҖдёӘеӯ—ҪWҰдёІеQҢжү“еҚ°еҮәиҜҘеӯ—ҪWҰдёІдёӯеӯ—ҪWҰзҡ„жүҖжңүжҺ’еҲ—гҖ?br />дҫӢеҰӮиҫ“е…Ҙеӯ—з¬ҰдёІabcеQҢеҲҷиҫ“еҮәз”ұеӯ—ҪWҰaгҖҒbгҖҒc жүҖиғҪжҺ’еҲ—еҮәжқҘзҡ„жүҖжңүеӯ—ҪWҰдёІ
abcгҖҒacbгҖҒbacгҖҒbcaгҖҒcab е’ҢcbaгҖ?/p>
еҲҶжһҗеQҡжӯӨйўҳжңҖеҲқж•ҙзҗҶдәҺеҺХd№ҙзҡ„еҫ®иҪҜйқўиҜ?00йўҳдёӯҪW?3йўҳпјҢҪW¬дәҢӢЖЎж•ҙзҗҶдәҺеҫ®иКYгҖҒGoogleҪ{үе…¬еҸ”RқһеёёеҘҪзҡ„йқўиҜ•йўҳеҸҠи§ЈҪ{”[ҪW?1-70йўҳ] ҪW?7йўҳгҖӮж— зӢ¬жңүеҒУһјҢҳqҷдёӘй—®йўҳд»Ҡе№ҙеҸҲеҮәзҺоCәҺд»Ҡе№ҙзҡ?011.10.09зҷ‘ЦәҰҪW”иҜ•йўҳдёӯгҖӮokеQҢжҺҘдёӢжқҘеQҢе’ұ们е…ҲеҘҪеҘҪеҲҶжһҗҳqҷдёӘй—®йўҳгҖ?br />
- дёҖгҖҒйҖ’еҪ’е®һзҺ°
д»ҺйӣҶеҗҲдёӯдҫқж¬ЎйҖүеҮәжҜҸдёҖдёӘе…ғзҙ пјҢдҪңдШ“жҺ’еҲ—зҡ„第дёҖдёӘе…ғзҙ пјҢ然еҗҺеҜ№еү©дҪҷзҡ„е…ғзҙ ҳqӣиЎҢе…ЁжҺ’еҲ—пјҢеҰӮжӯӨйҖ’еҪ’еӨ„зҗҶеQҢд»ҺиҖҢеҫ—еҲ°жүҖжңүе…ғзҙ зҡ„е…ЁжҺ’еҲ—гҖӮд»ҘеҜ№еӯ—ҪWҰдёІabcҳqӣиЎҢе…ЁжҺ’еҲ—дШ“дҫӢпјҢжҲ‘们еҸҜд»Ҙҳqҷд№ҲеҒҡпјҡд»ҘabcдёЮZҫӢ
еӣәе®ҡaеQҢжұӮеҗҺйқўbcзҡ„жҺ’еҲ—пјҡabcеQҢacbеQҢжұӮеҘҪеҗҺеQҢaе’ҢbдәӨжҚўеQҢеҫ—еҲ°bac
еӣәе®ҡbеQҢжұӮеҗҺйқўacзҡ„жҺ’еҲ—пјҡbacеQҢbcaеQҢжұӮеҘҪеҗҺеQҢcж”‘ЦҲ°ҪW¬дёҖдҪҚзҪ®еQҢеҫ—еҲ°cba
еӣәе®ҡcеQҢжұӮеҗҺйқўbaзҡ„жҺ’еҲ—пјҡcbaеQҢcabгҖӮд»Јз ҒеҸҜеҰӮдёӢҫ~–еҶҷжүҖҪCәпјҡ
- template <typename T>
- void CalcAllPermutation_R(T perm[], int first, int num)
- {
- if (num <= 1) {
- return;
- }
- for (int i = first; i < first + num; ++i) {
- swap(perm[i], perm[first]);
- CalcAllPermutation_R(perm, first + 1, num - 1);
- swap(perm[i], perm[first]);
- }
- }
- void Permutation(char* pStr, char* pBegin);
- void Permutation(char* pStr)
- {
- Permutation(pStr, pStr);
- }
- void Permutation(char* pStr, char* pBegin)
- {
- if(!pStr || !pBegin)
- return;
- if(*pBegin == '\0')
- {
- printf("%s\n", pStr);
- }
- else
- {
- for(char* pCh = pBegin; *pCh != '\0'; ++ pCh)
- {
- // swap pCh and pBegin
- char temp = *pCh;
- *pCh = *pBegin;
- *pBegin = temp;
- Permutation(pStr, pBegin + 1);
- // restore pCh and pBegin
- temp = *pCh;
- *pCh = *pBegin;
- *pBegin = temp;
- }
- }
- }
- дәҢгҖҒеӯ—е…ёеәҸжҺ’еҲ—
жҠҠеҚҮеәҸзҡ„жҺ’еҲ—еQҲеҪ“з„УһјҢд№ҹеҸҜд»Ҙе®һзҺоCШ“йҷҚеәҸеQүдҪңдёәеҪ“еүҚжҺ’еҲ—ејҖе§ӢпјҢ然еҗҺдҫқж¬Ўи®Ўз®—еҪ“еүҚжҺ’еҲ—зҡ„дёӢдёҖдёӘеӯ—е…ёеәҸжҺ’еҲ—гҖ?br />еҜ№еҪ“еүҚжҺ’еҲ—д»ҺеҗҺеҗ‘еүҚжү«жҸҸпјҢжү‘ЦҲ°дёҖеҜ№дШ“еҚҮеәҸзҡ„зӣёйӮХd…ғзҙ пјҢи®оCШ“iе’ҢjеQҲi < jеQүгҖӮеҰӮжһңдёҚеӯҳеңЁҳqҷж ·дёҖеҜ№дШ“еҚҮеәҸзҡ„зӣёйӮХd…ғзҙ пјҢеҲҷжүҖжңүжҺ’еҲ—еқҮе·ІжүҫеҲҺНјҢҪҺ—жі•ҫl“жқҹеQӣеҗҰеҲҷпјҢйҮҚж–°еҜ№еҪ“еүҚжҺ’еҲ—д»ҺеҗҺеҗ‘еүҚжү«жҸҸпјҢжү‘ЦҲ°ҪW¬дёҖдёӘеӨ§дәҺiзҡ„е…ғзҙ kеQҢдәӨжҚўiе’ҢkеQҢ然еҗҺеҜ№д»ҺjејҖе§ӢеҲ°ҫl“жқҹзҡ„еӯҗеәҸеҲ—еҸҚиқ{еQҢеҲҷжӯӨж—¶еҫ—еҲ°зҡ„ж–°жҺ’еҲ—һ®ЧғШ“дёӢдёҖдёӘеӯ—е…ёеәҸжҺ’еҲ—гҖӮиҝҷҝUҚж–№ејҸе®һзҺ°еҫ—еҲ°зҡ„жүҖжңүжҺ’еҲ—жҳҜжҢүеӯ—е…ёеәҸжңүеәҸзҡ„пјҢҳqҷд№ҹжҳҜC++ STLҪҺ—жі•next_permutationзҡ„жҖқжғігҖӮз®—жі•е®һзҺ°еҰӮдёӢпјҡ
- template <typename T>
- void CalcAllPermutation(T perm[], int num)
- {
- if (num < 1)
- return;
- while (true) {
- int i;
- for (i = num - 2; i >= 0; --i) {
- if (perm[i] < perm[i + 1])
- break;
- }
- if (i < 0)
- break; // е·Із»Ҹжү‘ЦҲ°жүҖжңүжҺ’еҲ?/span>
- int k;
- for (k = num - 1; k > i; --k) {
- if (perm[k] > perm[i])
- break;
- }
- swap(perm[i], perm[k]);
- reverse(perm + i + 1, perm + num);
- }
- }
иҪ¬иҮӘ http://blog.csdn.net/v_july_v/article/details/6879101
ҫUўй»‘ж ‘зҡ„тqҢҷЎЎ
ҫUўй»‘ж ‘йҰ–е…ҲжҳҜдёҖӢӮөдәҢеҸүжҹҘжүҫж ‘еQҢе®ғжҜҸдёӘҫl“зӮ№йғҪиў«ж ҮдёҠдәҶйўңиүФҢјҲҫUўиүІжҲ–й»‘иүФҢјүеQҢзәўй»‘ж ‘ж»Ўиғцд»ҘдёӢ5дёӘжҖ§иҙЁеQ?/span>
1гҖ?nbsp;жҜҸдёӘҫl“зӮ№зҡ„йўңиүІеҸӘиғҪжҳҜҫUўиүІжҲ–й»‘иүҢУҖ?/span>
2гҖ?nbsp;ж №з»“зӮТҺҳҜй»‘иүІзҡ„гҖ?/span>
3гҖ?nbsp;жҜҸдёӘеҸ¶еӯҗҫl“зӮ№йғҪеёҰжңүдёӨдёӘз©әзҡ„й»‘иүІз»“зӮ№пјҲиў«з§°дёәй»‘е“Ёе…өеQүпјҢеҰӮжһңдёҖдёӘз»“зӮ?/span>nзҡ„еҸӘжңүдёҖдёӘе·Ұеӯ©еӯҗеQҢйӮЈд№?/span>nзҡ„еҸіеӯ©еӯҗжҳҜдёҖдёӘй»‘е“Ёе…өеQӣеҰӮжһңз»“зӮ?/span>nеҸӘжңүдёҖдёӘеҸіеӯ©еӯҗеQҢйӮЈд№?/span>nзҡ„е·Ұеӯ©еӯҗжҳҜдёҖдёӘй»‘е“Ёе…өгҖ?/span>
4гҖ?nbsp;еҰӮжһңдёҖдёӘз»“зӮТҺҳҜҫUўзҡ„еQҢеҲҷе®ғзҡ„дёӨдёӘе„ҝеӯҗйғҪжҳҜй»‘зҡ„гҖӮд№ҹһ®ұжҳҜиҜҙеңЁдёҖжқЎиө\еҫ„дёҠдёҚиғҪеҮәзҺ°зӣ”RӮ»зҡ„дёӨдёӘзәўиүІз»“зӮҸVҖ?/span>
5гҖ?nbsp;еҜ№дәҺжҜҸдёӘҫl“зӮ№жқҘиҜҙеQҢд»ҺиҜҘз»“зӮ№еҲ°е…¶еӯҗеӯҷеҸ¶ҫl“зӮ№зҡ„жүҖжңүиө\еҫ„дёҠеҢ…еҗ«зӣёеҗҢж•°зӣ®зҡ„й»‘ҫl“зӮ№гҖ?/span>
ҫUўй»‘ж ‘зҡ„ҳq?/span>5дёӘжҖ§иҙЁдёӯпјҢҪW?/span>3зӮТҺҳҜжҜ”иҫғйҡ„ЎҗҶи§Јзҡ„еQҢдҪҶе®ғеҚҙйқһеёёжңүеҝ…иҰҒгҖӮжҲ‘们зңӢеӣ?/span>1дёӯзҡ„е·Ұиҫ№ҳqҷеј еӣҫпјҢеҰӮжһңдёҚдӢЙз”Ёй»‘е“Ёе…өеQҢе®ғе®Ңе…Ёж»ЎиғцҫUўй»‘ж ‘жҖ§иҙЁеQҢз»“зӮ?/span>50еҲоCёӨдёӘеҸ¶ҫl“зӮ№8е’ҢеҸ¶ҫl“зӮ№82и·Ҝеҫ„дёҠзҡ„й»‘иүІҫl“зӮ№ж•°йғҪдё?/span>2дёӘгҖӮдҪҶеҰӮжһңеҠ е…Ҙй»‘е“Ёе…өеҗҺеQҲеҰӮеӣ?/span>1еҸӣ_ӣҫдёӯзҡ„һ®Ҹй»‘еңҶзӮ№еQүпјҢеҸ¶з»“зӮ№зҡ„дёӘж•°еҸҳдШ“8дёӘй»‘е“Ёе…өеQҢж №ҫl“зӮ№50еҲ°иҝҷ8дёӘеҸ¶ҫl“зӮ№и·Ҝеҫ„дёҠзҡ„й»‘й«ҳеәҰе°ұдёҚдёҖж ·дәҶеQҢжүҖд»Ҙе®ғтq¶дёҚжҳҜдёҖӢӮлҠәўй»‘ж ‘гҖ?/span>
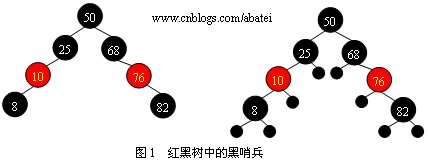
иҰҒзңӢзңҹжӯЈзҡ„зәўй»‘ж ‘иҜ·еңЁд»ҘдёҠеҠЁз”»дёӯж·»еҠ еҮ дёӘз»“зӮ№пјҢзңӢзңӢжҳҜеҗҰж»Ўиғцд»ҘдёҠжҖ§иҙЁгҖ?/span>
ҫUўй»‘ж ‘зҡ„ж—Ӣиқ{ж“ҚдҪң
ҫUўй»‘ж ‘зҡ„ж—Ӣиқ{ж“ҚдҪңе’?/span>AVLж ‘дёҖж шPјҢеҲҶдШ“LLгҖ?/span>RRгҖ?/span>LRгҖ?/span>RLеӣӣз§Қж—Ӣиқ{ҫcХdһӢеQҢе·®еҲ«еңЁдәҺж—ӢиҪ¬е®ҢжҲҗеҗҺж”№еҸҳзҡ„жҳҜҫl“зӮ№зҡ„йўңиүФҢјҢиҖҢдёҚжҳҜег^иЎЎеӣ еӯҗгҖӮж—ӢиҪ¬еҠЁз”АLј”ҪCшҷҜ·еҸӮиҖ?/span>AVLҳqҷзҜҮж–Үз« дёӯзҡ„FlashеҠЁз”»еQ?/span>
http://www.cnblogs.com/abatei/archive/2008/11/17/1335031.html
ҫUўй»‘ж ‘дёҠҫl“зӮ№зҡ„жҸ’е…?/span>
еңЁи®Ёи®әзәўй»‘ж ‘зҡ„жҸ’е…Ҙж“ҚдҪңд№ӢеүҚеҝ…ҷе»иҰҒжҳҺзҷҪеQҢд“QдҪ•дёҖдёӘеҚіһ®ҶжҸ’е…Ҙзҡ„ж–°з»“зӮ№зҡ„еҲқе§ӢйўңиүІйғҪдШ“ҫUўиүІгҖӮиҝҷдёҖзӮ№еҫҲе®ТҺҳ“зҗҶи§ЈеQҢеӣ дёәжҸ’е…Ҙй»‘зӮ№дјҡеўһеҠ жҹҗжқЎи·Ҝеҫ„дёҠй»‘ҫl“зӮ№зҡ„ж•°зӣ®пјҢд»ҺиҖҢеҜјиҮҙж•ҙӢӮү| ‘й»‘й«ҳеәҰзҡ„дёҚег^иЎЎгҖӮдҪҶеҰӮжһңж–°з»“зӮ№зҲ¶ҫl“зӮ№дёәзәўиүІж—¶еQҲеҰӮеӣ?/span>2жүҖҪCәпјүеQҢе°Ҷдјҡиҝқҳq”зәўй»‘ж ‘жҖ§иҙЁеQҡдёҖжқЎиө\еҫ„дёҠдёҚиғҪеҮәзҺ°зӣ”RӮ»зҡ„дёӨдёӘзәўиүІз»“зӮҸVҖӮиҝҷж—¶е°ұйңҖиҰҒйҖҡиҝҮдёҖҫpХdҲ—ж“ҚдҪңжқҘдӢЙҫUўй»‘ж ‘дҝқжҢҒег^иЎЎгҖ?/span>

дёЮZәҶжё…жҘҡең°иЎЁҪCәжҸ’е…Ҙж“ҚдҪңд»ҘдёӢеңЁҫl“зӮ№дёӯдӢЙз”?#8220;ж–?#8221;еӯ—иЎЁҪCЮZёҖдёӘж–°жҸ’е…Ҙзҡ„з»“зӮ№пјӣдҪҝз”Ё“зҲ?#8221;еӯ—иЎЁҪCәж–°жҸ’е…ҘзӮ№зҡ„зҲ¶з»“зӮ№пјӣдҪҝз”Ё“еҸ?#8221;еӯ—иЎЁҪC?#8220;зҲ?#8221;ҫl“зӮ№зҡ„е…„ејҹз»“зӮ№пјӣдҪҝз”Ё“јң?#8221;еӯ—иЎЁҪC?#8220;зҲ?#8221;ҫl“зӮ№зҡ„зҲ¶ҫl“зӮ№гҖӮжҸ’е…Ҙж“ҚдҪңеҲҶдёЮZ»ҘдёӢеҮ ҝUҚжғ…еҶөпјҡ
1гҖ?/span>й»‘зҲ¶
еҰӮеӣҫ3жүҖҪCәпјҢеҰӮжһңж–°зӮ№зҡ„зҲ¶ҫl“зӮ№дёәй»‘иүІз»“зӮ№пјҢйӮЈд№ҲжҸ’е…ҘдёҖдёӘзәўзӮ№е°ҶдёҚдјҡеҪұе“ҚҫUўй»‘ж ‘зҡ„тqҢҷЎЎеQҢжӯӨж—¶жҸ’е…Ҙж“ҚдҪңе®ҢжҲҗгҖӮзәўй»‘ж ‘жҜ?/span>AVLж ‘дјҳҝUҖзҡ„ең°ж–№д№ӢдёҖеңЁдәҺй»‘зҲ¶зҡ„жғ…еҶү|Ҝ”иҫғеёёи§ҒпјҢд»ҺиҖҢдӢЙҫUўй»‘ж ‘йңҖиҰҒж—ӢиҪ¬зҡ„еҮ зҺҮзӣёеҜ№AVLж ‘жқҘиҜҙдјҡһ®‘дёҖдәӣгҖ?/span>
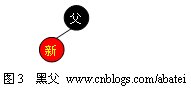
2еQҺзәўзҲ?/span>
еҰӮжһңж–°зӮ№зҡ„зҲ¶ҫl“зӮ№дёәзәўиүФҢјҢҳqҷж—¶һ®ұйңҖиҰҒиҝӣиЎҢдёҖҫpХdҲ—ж“ҚдҪңд»ҘдҝқиҜҒж•ҙӢӮү| ‘ҫUўй»‘жҖ§иҙЁгҖӮеҰӮеӣ?/span>3жүҖҪCәпјҢз”ЧғәҺзҲ¶з»“зӮ№дШ“ҫUўиүІеQҢжӯӨж—¶еҸҜд»ҘеҲӨе®ҡпјҢјң–зҲ¶ҫl“зӮ№еҝ…е®ҡдёәй»‘иүҢУҖӮиҝҷж—үҷңҖиҰҒж №жҚ®еҸ”зҲ¶з»“зӮ№зҡ„йўңиүІжқҘеҶіе®ҡеҒҡд»Җд№Ҳж ·зҡ„ж“ҚдҪңгҖӮйқ’иүІз»“зӮ№иЎЁҪCәйўңиүІжңӘзҹҘгҖӮз”ұдәҺжңүеҸҜиғҪйңҖиҰҒж №ҫl“зӮ№еҲ°ж–°зӮ№зҡ„и·Ҝеҫ„дёҠиҝӣиЎҢеӨҡӢЖЎж—ӢиҪ¬ж“ҚдҪңпјҢиҖҢжҜҸӢЖЎиҝӣиЎҢдёҚтqҢҷЎЎеҲӨж–ӯзҡ„и“vе§ӢзӮ№еQҲжҲ‘们еҸҜһ®Ҷе…¶и§ҶдШ“ж–°зӮ№еQүйғҪдёҚдёҖж —чҖӮжүҖд»ҘжҲ‘们еңЁжӯӨдӢЙз”ЁдёҖдёӘи“қиүІз®ӯеӨҙжҢҮеҗ‘иҝҷдёӘи“vе§ӢзӮ№еQҢеЖҲҝUоC№ӢдёәеҲӨе®ҡзӮ№гҖ?/span>
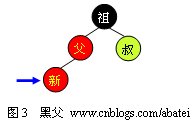
2.1 ҫUўеҸ”
еҪ“еҸ”зҲ¶з»“зӮ№дШ“ҫUўиүІж—УһјҢеҰӮеӣҫ4жүҖҪCәпјҢж— йңҖҳqӣиЎҢж—Ӣиқ{ж“ҚдҪңеQҢеҸӘиҰҒе°ҶзҲ¶е’ҢеҸ”з»“зӮ№еҸҳдёәй»‘иүФҢјҢһ®ҶзҘ–зҲ¶з»“зӮ№еҸҳдёәзәўиүІеҚіеҸҜгҖӮдҪҶз”ЧғәҺјң–зҲ¶ҫl“зӮ№зҡ„зҲ¶ҫl“зӮ№жңүеҸҜиғҪдШ“ҫUўиүІеQҢд»ҺиҖҢиҝқеҸҚзәўй»‘ж ‘жҖ§иҙЁгҖӮжӯӨж—¶еҝ…ҷеХd°Ҷјң–зҲ¶ҫl“зӮ№дҪңдШ“ж–°зҡ„еҲӨе®ҡзӮ№з‘фҫlӯеҗ‘дёҠиҝӣиЎҢег^иЎЎж“ҚдҪңгҖ?/span>
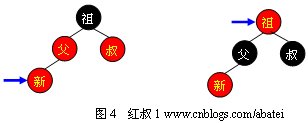
йңҖиҰҒжіЁж„ҸпјҢж— и®ә“зҲ?#8221;ең?#8220;еҸ?#8221;зҡ„е·Ұиҫ№иҝҳжҳҜеҸіиҫ№пјҢж— и®ә“ж–?#8221;жҳ?#8220;зҲ?#8221;зҡ„е·Ұеӯ©еӯҗҳqҳжҳҜеҸӣ_ӯ©еӯҗпјҢе®ғ们зҡ„ж“ҚдҪңйғҪе®Ңе…ЁдёҖж —чҖ?/span>
2.2 й»‘еҸ”
еҪ“еҸ”зҲ¶з»“зӮ№дШ“й»‘иүІж—УһјҢйңҖиҰҒиҝӣиЎҢж—ӢиҪ¬пјҢд»ҘдёӢеӣ„ЎӨәдәҶжүҖжңүзҡ„ж—Ӣиқ{еҸҜиғҪ
жғ…еЕһ1еQ?/span>
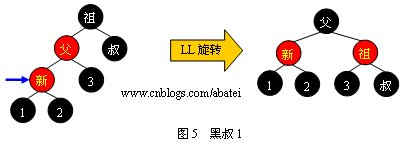
жғ…еЕһ2еQ?/span>
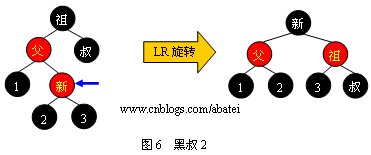
жғ…еЕһ3еQ?/span>
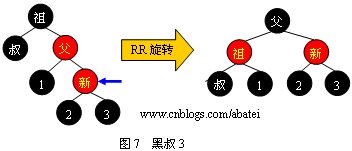
жғ…еЕһ4еQ?/span>
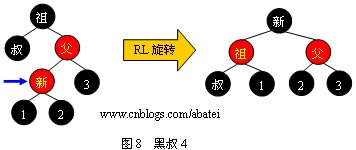
еҸҜд»Ҙи§ӮеҜҹеҲҺНјҢеҪ“ж—ӢиҪ¬е®ҢжҲҗеҗҺеQҢж–°зҡ„ж—ӢиҪ¬ж №е…ЁйғЁдёәй»‘иүФҢјҢжӯӨж—¶дёҚйңҖиҰҒеҶҚеҗ‘дёҠеӣһжәҜҳqӣиЎҢтqҢҷЎЎж“ҚдҪңеQҢжҸ’е…Ҙж“ҚдҪңе®ҢжҲҗгҖӮйңҖиҰҒжіЁж„ҸпјҢдёҠйқўеӣӣеј еӣ„Ўҡ„“еҸ?#8221;гҖ?#8220;1”гҖ?#8220;2”гҖ?#8220;3”ҫl“зӮ№жңүеҸҜиғҪдШ“й»‘е“Ёе…лҠ»“зӮҸVҖ?/span>
е…¶е®һҫUўй»‘ж ‘зҡ„жҸ’е…Ҙж“ҚдҪңдёҚжҳҜеҫҲйҡҫеQҢз”ҡиҮПxҜ”AVLж ‘зҡ„жҸ’е…Ҙж“ҚдҪңҳqҳжӣҙҪҺҖеҚ•дәӣгҖӮдҪҶеҲ йҷӨж“ҚдҪңһ®ЮpҝңҳqңжҜ”AVLж ‘еӨҚжқӮеҫ—еӨҡпјҢдёӢйқўһ®Чғ»ӢҫlҚзәўй»‘ж ‘зҡ„еҲ йҷӨж“ҚдҪңгҖ?/span>
ҫUўй»‘ж ‘дёҠҫl“зӮ№зҡ„еҲ йҷ?/span>
ҫUўй»‘ж ‘жң¬нw«жҳҜдёҖӢӮөдәҢеҸүжҹҘжүҫж ‘еQҢе®ғзҡ„еҲ йҷӨе’ҢдәҢеҸүжҹҘжүҫж ‘зҡ„еҲ йҷӨҫcЦMјјгҖӮйҰ–е…ҲиҰҒжү‘ЦҲ°зңҹжӯЈзҡ„еҲ йҷӨзӮ№еQҢеҪ“иў«еҲ йҷӨз»“зӮ?/span>nеӯҳеңЁе·ҰеҸіеӯ©еӯҗж—УһјҢзңҹжӯЈзҡ„еҲ йҷӨзӮ№еә”иҜҘжҳ?/span>nзҡ„дёӯеәҸйҒҚеңЁеүҚй©ұпјҢе…ідәҺҳqҷдёҖзӮ№иҜ·еӨҚд№ дәҢеҸүжҹҘжүҫж ‘зҡ„еҲ йҷӨгҖӮеҰӮеӣ?/span>9жүҖҪCәпјҢеҪ“еҲ йҷӨз»“зӮ?/span>20ж—УһјҢе®һйҷ…иў«еҲ йҷӨзҡ„ҫl“зӮ№еә”иҜҘдё?/span>18еQҢз»“зӮ?/span>20зҡ„ж•°жҚ®еҸҳдё?/span>18гҖ?/span>
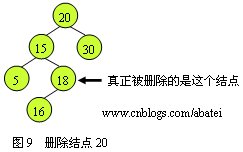
жүҖд»ҘеҸҜд»ҘжҺЁж–ӯеҮәеQҢеңЁҳqӣиЎҢеҲ йҷӨж“ҚдҪңж—УһјҢзңҹжӯЈзҡ„еҲ йҷӨзӮ№еҝ…е®ҡжҳҜеҸӘжңүдёҖдёӘеӯ©еӯҗжҲ–жІЎжңүеӯ©еӯҗзҡ„з»“зӮҸVҖӮиҖҢж №жҚ®зәўй»‘ж ‘зҡ„жҖ§иҙЁеҸҜд»Ҙеҫ—еҮәд»ҘдёӢдёӨдёӘҫl“и®әеQ?/span>
1гҖ?nbsp;еҲ йҷӨж“ҚдҪңдёӯзңҹжӯЈиў«еҲ йҷӨзҡ„еҝ…е®ҡжҳҜеҸӘжңүдёҖдёӘзәўиүІеӯ©еӯҗжҲ–жІЎжңүеӯ©еӯҗзҡ„з»“зӮ?/span>гҖ?/span>
2гҖ?nbsp;еҰӮжһңзңҹжӯЈзҡ„еҲ йҷӨзӮ№жҳҜдёҖдёӘзәўиүІз»“зӮ№пјҢйӮЈд№Ҳе®ғеҝ…е®ҡжҳҜдёҖдёӘеҸ¶еӯҗз»“зӮ?/span>гҖ?/span>
зҗҶи§ЈҳqҷдёӨзӮҡwқһеё”RҮҚиҰҒпјҢеҰӮеӣҫ10жүҖҪCәпјҢйҷӨдәҶжғ…еҶө(a)еӨ–пјҢе…¶д»–д»ЦMёҖҝUҚеҶөҫl“зӮ№NйғҪж— жі•ж»Ўӯ‘ізәўй»‘ж ‘жҖ§иҙЁгҖ?/span>
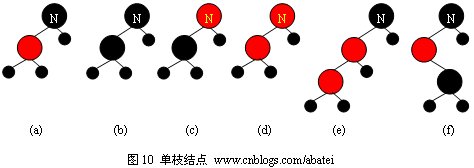
еңЁд»ҘдёӢи®Ёи®ЮZёӯеQҢжҲ‘们дӢЙз”Ёи“қиүІз®ӯеӨҙиЎЁҪCәзңҹжӯЈзҡ„еҲ йҷӨзӮ№пјҢе®ғд№ҹжҳҜж—ӢиҪ¬ж“ҚдҪңиҝҮҪEӢдёӯзҡ„第дёҖдёӘеҲӨе®ҡзӮ№еQӣзңҹжӯЈзҡ„еҲ йҷӨзӮ№дӢЙз”?#8220;ж—?#8221;ж ҮжіЁеQҢж—§зӮТҺүҖеңЁдҪҚҫ|®е°Ҷиў«е®ғзҡ„зҡ„еӯ©еӯҗҫl“зӮ№жүҖеҸ–д»ЈеQҲжңҖеӨҡеҸӘжңүдёҖдёӘеӯ©еӯҗпјүеQҢжҲ‘们дӢЙз”?#8220;ж–?#8221;иЎЁзӨәж—§зӮ№зҡ„еӯ©еӯҗз»“зӮҸVҖӮеҲ йҷӨж“ҚдҪңеҸҜеҲҶдШ“д»ҘдёӢеҮ з§Қжғ…еЕһеQ?/span>
1гҖҒж—§зӮ№дШ“ҫUўиүІҫl“зӮ№
иӢҘж—§зӮ№дШ“ҫUўиүІҫl“зӮ№еQҢеҲҷе®ғеҝ…е®ҡжҳҜеҸ¶еӯҗҫl“зӮ№еQҢзӣҙжҺҘеҲ йҷӨеҚіеҸҜгҖӮеҰӮеӣ?/span>11жүҖҪC?/span>
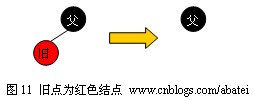
2гҖҒдёҖҫUўдёҖй»?/span>
еҪ“ж—§зӮ№дШ“й»‘иүІҫl“зӮ№еQҢж–°зӮ№дШ“ҫUўиүІҫl“зӮ№ж—УһјҢһ®Ҷж–°зӮ№еҸ–д»Јж—§зӮ№дҪҚҫ|®еҗҺеQҢе°Ҷж–°зӮ№жҹ“жҲҗй»‘иүІеҚӣ_ҸҜеQҲеҰӮеӣ?/span>12жүҖҪCәпјүгҖӮиҝҷйҮҢйңҖиҰҒжіЁж„Ҹпјҡж—§зӮ№дёәзәўиүФҢјҢж–°зӮ№дёәй»‘иүІзҡ„жғ…еҶөдёҚеҸҜиғҪеӯҳеңЁгҖ?/span>
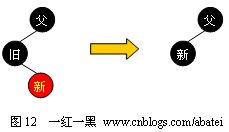
3гҖҒеҸҢй»?/span>
еҪ“ж—§зӮ№е’Ңж–°зӮ№йғҪдШ“й»‘иүІж—УһјҲж–°зӮ№дёәз©әҫl“зӮ№ж—УһјҢдәҰеұһдәҺиҝҷҝUҚжғ…еҶөпјүеQҢжғ…еҶү|Ҝ”иҫғеӨҚжқӮпјҢйңҖиҰҒж №жҚ®ж—§зӮ№е…„ејҹз»“зӮ№зҡ„йўңиүІжқҘеҶіе®ҡиҝӣиЎҢд»Җд№Ҳж ·зҡ„ж“ҚдҪңгҖӮжҲ‘们дӢЙз”?#8220;е…?#8221;жқҘиЎЁҪCәж—§зӮ№зҡ„е…„ејҹҫl“зӮ№гҖӮиҝҷйҮҢеҸҜеҲҶдШ“ҫUўе…„е’Ңй»‘е…„дёӨҝUҚжғ…еҶөпјҡ
3.1 ҫUўе…„
з”ЧғәҺе…„ејҹҫl“зӮ№дёәзәўиүФҢјҢжүҖд»ҘзҲ¶ҫl“зӮ№еҝ…е®ҡдёәй»‘иүФҢјҢиҖҢж—§зӮ№иў«еҲ йҷӨеҗҺпјҢж–°зӮ№еҸ–д»ЈдәҶе®ғзҡ„дҪҚҫ|®гҖӮдёӢеӣҫжј”ҪCЮZәҶдёӨз§ҚеҸҜиғҪзҡ„жғ…еҶөпјҡ
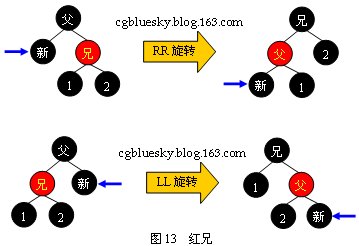
ҫUўе…„зҡ„жғ…еҶөйңҖиҰҒиҝӣиЎ?/span>RRжҲ?/span>LLеһӢж—ӢиҪ¬пјҢ然еҗҺһ®ҶзҲ¶ҫl“зӮ№жҹ“жҲҗҫUўиүІеQҢе…„ҫl“зӮ№жҹ“жҲҗй»‘иүІгҖӮ然еҗҺйҮҚж–оC»Ҙж–°зӮ№дёәеҲӨе®ҡзӮ№ҳqӣиЎҢтqҢҷЎЎж“ҚдҪңгҖӮжҲ‘们еҸҜд»Ҙи§ӮеҜҹеҲ°еQҢж—ӢиҪ¬ж“ҚдҪңе®ҢжҲҗеҗҺеQҢеҲӨе®ҡзӮ№жІЎжңүеҗ‘дёҠеӣһжәҜеQҢиҖҢжҳҜйҷҚдҪҺдәҶдёҖеұӮпјҢжӯӨж—¶еҸҳжҲҗдәҶй»‘е…„зҡ„жғ…еҶөгҖ?/span>
3.2 й»‘е…„
й»‘е…„зҡ„жғ…еҶү|ңҖдёәеӨҚжқӮпјҢйңҖиҰҒж №жҚ®й»‘е…„еӯ©еӯҗз»“зӮ№пјҲҳqҷйҮҢз”?#8220;дҫ?#8221;иЎЁзӨәеQүе’ҢзҲ¶дәІҫl“зӮ№зҡ„йўңиүІжқҘеҶӣ_®ҡеҒҡд»Җд№Ҳж ·зҡ„ж“ҚдҪңгҖ?/span>
3.2.1 й»‘е…„дәҢй»‘дҫ„зәўзҲ?/span>
еҰӮеӣҫ14жүҖҪCәпјҢҳqҷз§Қжғ…еҶөжҜ”иҫғҪҺҖеҚ•пјҢеҸӘйңҖһ®ҶзҲ¶ҫl“зӮ№еҸҳдШ“й»‘иүІеQҢе…„ҫl“зӮ№еҸҳдШ“й»‘иүІеQҢж–°ҫl“зӮ№еҸҳдШ“й»‘иүІеҚӣ_ҸҜеQҢеҲ йҷӨж“ҚдҪңеҲ°жӯӨз»“жқҹгҖ?/span>
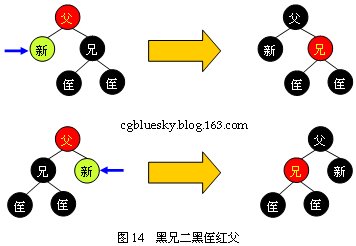
3.2.2 й»‘е…„дәҢй»‘дҫ„й»‘зҲ?/span>
еҰӮеӣҫ15жүҖҪCәпјҢжӯӨж—¶һ®ҶзҲ¶ҫl“зӮ№жҹ“жҲҗж–°з»“зӮ№зҡ„йўңиүІеQҢж–°ҫl“зӮ№жҹ“жҲҗй»‘иүІеQҢе…„ҫl“зӮ№жҹ“жҲҗҫUўиүІеҚӣ_ҸҜгҖӮеҪ“ж–°з»“зӮ№дШ“ҫUўиүІж—УһјҢзҲ¶з»“зӮ№иў«жҹ“жҲҗҫUўиүІеQҢжӯӨж—үҷңҖиҰҒд»ҘзҲ¶з»“зӮ№дШ“еҲӨе®ҡзӮ№з‘фҫlӯеҗ‘дёҠиҝӣиЎҢег^иЎЎж“ҚдҪңгҖ?/span>
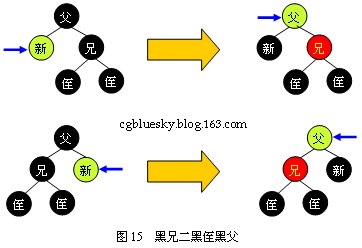
3.2.3 й»‘е…„ҫUўдҫ„
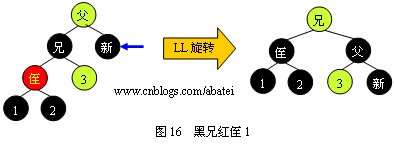
й»‘е…„ҫUўдҫ„жңүд»ҘдёӢеӣӣҝUҚжғ…еҪўпјҢдёӢйқўеҲҶеҲ«ҳqӣиЎҢеӣ„ЎӨәеQ?/span>
жғ…еЕһ1еQ?/span>
жғ…еЕһ2еQ?/span>
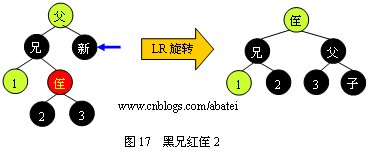
жғ…еЕһ3еQ?/span>

жғ…еЕһ4еQ?/span>
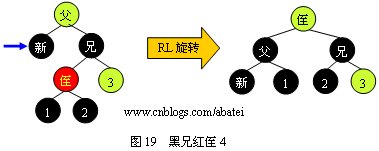
з”Чғ»ҘдёҠеӣҫдҫӢжүҖҪCәпјҢзңӢе®Ңд»ҘдёҠеӣӣеј еӣ„Ўҡ„е…„ејҹжңүеҸҜиғҪдјҡжңүдёҖдёӘз–‘й—®пјҢеҰӮжһңжғ…еЕһ1е’Ңжғ…еҪ?/span>2дёӯзҡ„дёӨдёӘдҫ„еӯҗҫl“зӮ№йғҪдШ“ҫUўиүІж—УһјҢжҳҜиҜҘҳqӣиЎҢLLж—Ӣиқ{ҳqҳжҳҜҳqӣиЎҢLRж—Ӣиқ{е‘ўпјҹҪ{”жЎҲжҳҜиҝӣиЎ?/span>LLж—Ӣиқ{гҖӮжғ…еҪ?/span>3е’Ңжғ…еҪ?/span>4еҲҷжҳҜдјҳе…ҲҳqӣиЎҢRRж—Ӣиқ{зҡ„еҲӨе®ҡгҖ?br />ҫUўй»‘ж ‘зҡ„д»Јз Ғе®һзҺ°