Mandelbrot集合是在復平面組成分形的點的集合,用復二次多項式  來定義
來定義
其中c是一個復參數。對于每一個c,從 開始對fc(z)進行迭代。
開始對fc(z)進行迭代。
序列 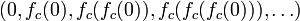 的元素的模(復數具有模的概念)或者延伸到無窮大,或者只停留在有限半徑的圓盤內。Mandelbrot集合就是使以上序列不延伸至無限大的所有c點的集合。
的元素的模(復數具有模的概念)或者延伸到無窮大,或者只停留在有限半徑的圓盤內。Mandelbrot集合就是使以上序列不延伸至無限大的所有c點的集合。
簡單來說,對于迭代式:fc(z) = z2 + c ,Mandelbrot Set 迭代過程中的z值是固定的,是使上述迭代式始終在某一范圍內而不發散于無窮大的c值的集
合;而Julia Set的迭代過程中c是固定的,上述是使上述迭代式始終在某一范圍內而不發散于無窮大的z值的集合。
從數學上來講,Mandelbrot集合是一個復數的集合。一個給定的復數c或者屬于Mandelbrot集合M,或者不屬于。比如,取c = 1,那么這個序列就是(0, 1, 2, 5, 26, ...),顯然它的值會趨于無窮大;而如果取c = i,那么序列就是(0, i, -1+i, -i, -1+i, -i,...),它的值會一直停留在有限半徑的圓盤內。
事實上,一個點屬于Mandelbrot集合當且僅當它對應的序列(由上面的二項式定義)中的任何元素的模都不大于2。這里的2就是上面提到的“有限半徑”。
在計算機上繪制Mandelbrot集合
計算機的屏幕上的像素只有有限個,而Mandelbrot集合中的點則有無限個。
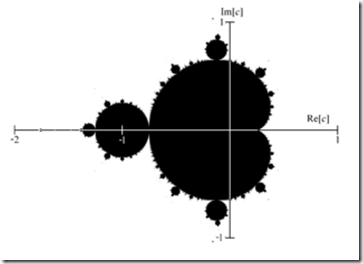
觀察上面復平面的局部,Mandelbrot集合即黑色區域,實部從-2到1,虛部從-1到1,那么將兩個點(-2, 1)和(1, -1)作為一個矩形的左上角頂點和右下角頂點,那么這個矩形就包含了整個Mandelbrot集合,該矩形的長為3,寬為2。我們可以將這個矩形與屏幕上的區域進行映射,也就是將屏幕上的一個像素映射為該矩形內的一點,如果該點屬于Mandelbrot集合,就將該像素著為黑色,這樣逐一對每個像素進行判斷和著色,就可以模擬繪制Mandelbrot集合了。該矩形的長寬比為3:2,我們在屏幕上可以取600 * 400的矩形區域。
完成映射后來考慮如何判斷一個點是否屬于該集合。其根據就是上面的結論“一個點屬于Mandelbrot集合當且僅當它對應的序列(由上面的二項式定義)中的任何元素的模都不大于2”,由于序列的的元素有無窮多個,我們只能取有限的迭代次數來模擬了,比如取100或1000次。
一個基本的Mandelbrot set的繪制<基于OpenGL>,沒有設置復雜的顏色

一個給點著色的Mandelbrot set的繪制<基于OpenGL>
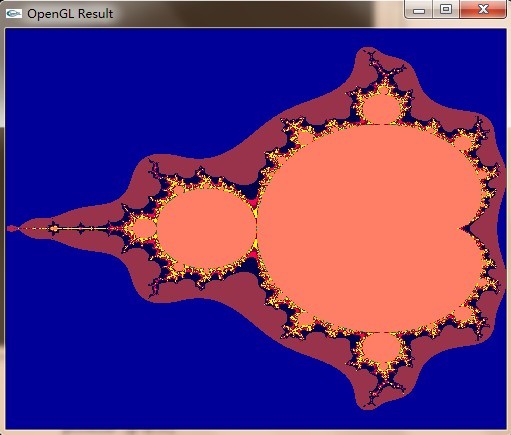
一個給點著色的Mandelbrot set的繪制 三次 <基于OpenGL>
