1 首先是傅里葉級數(shù) Fourier Series
http://en.wikipedia.org/wiki/Fourier_series
需要理解明白就好，三角函數(shù)系的正交性。其實從三角函數(shù)系的正交性可以拓展到一般線性空間中的正交陣，從正交矩陣的逆是通過轉(zhuǎn)置實現(xiàn)來考慮傅里葉變換的逆(更一般的可以考慮酋矩陣來擴展到復(fù)線性空間)
任何連續(xù)測量的時序或信號，都可以表示為不同頻率的正弦波信號的無限疊加
2 下面是傅里葉變換的意義。
The motivation for the Fourier transform comes from the study of Fourier series. In the study of Fourier series, complicated periodic functions are written as the sum of simple waves mathematically represented by sines and cosines. Due to the properties of sine and cosine it is possible to recover the amount of each wave in the sum by an integral. In many cases it is desirable to use , which states that e2πiθ = cos 2πθ + i sin 2πθ, to write Fourier series in terms of the basic wavese2πiθ. This has the advantage of simplifying many of the formulas involved and providing a formulation for Fourier series that more closely resembles the definition followed in this article. This passage from sines and cosines to complex exponentials makes it necessary for the Fourier coefficients to be complex valued. The usual interpretation of this complex number is that it gives both the amplitude (or size) of the wave present in the function and the phase (or the initial angle) of the wave. This passage also introduces the need for negative "frequencies". If θ were measured in seconds then the waves e2πiθ and e?2πiθ would both complete one cycle per second, but they represent different frequencies in the Fourier transform. Hence, frequency no longer measures the number of cycles per unit time, but is closely related.
其實傅里葉變換的關(guān)鍵是什么？頻率抽取！在我看來。。
先看一下公式吧。。：
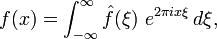
有人不明白。。為什么會引入復(fù)數(shù)。。你可以考慮一下歐拉公式。。上面的wiki上說的已經(jīng)很明白了。。
為什么說是頻率抽取，看一下公式， 如果讓自變量為1 ，把f(x)表示為三角函數(shù)形式。。那么根據(jù)三角函數(shù)正交性，則很容易得出，此時獲得的是，是經(jīng)過了e(-2PI I x )抽取之后的值，這個就是頻率抽取的意義。此時獲得的值，就是在所有的時域或者空域空間中，抽取了頻率為1 的值！！
OK，明白了這個，那么關(guān)鍵問題就解決了。。剩下的關(guān)于離散傅里葉變換，周期函數(shù)的傅里葉變換，連續(xù)的等等之類，都可類推。。可以參考下面的文章！
有下面的這篇文章，說的也不錯。。。
http://blog.chinaunix.net/u3/97043/showart_1959937.html
http://hi.baidu.com/yb223732/blog/item/a9ee11fa10ca4818a9d31147.html
1、為什么要進行傅里葉變換，其物理意義是什么？
傅立葉變換是數(shù)字信號處理領(lǐng)域一種很重要的算法。要知道傅立葉變換算法的意義，首先要了解傅立葉原理的意義。傅立葉原理表明：任何連續(xù)測量的時序或信號，都可以表示為不同頻率的正弦波信號的無限疊加。而根據(jù)該原理創(chuàng)立的傅立葉變換算法利用直接測量到的原始信號，以累加方式來計算該信號中不同正弦波信號的頻率、振幅和相位。
和傅立葉變換算法對應(yīng)的是反傅立葉變換算法。該反變換從本質(zhì)上說也是一種累加處理，這樣就可以將單獨改變的正弦波信號轉(zhuǎn)換成一個信號。
因此，可以說，傅立葉變換將原來難以處理的時域信號轉(zhuǎn)換成了易于分析的頻域信號（信號的頻譜），可以利用一些工具對這些頻域信號進行處理、加工。最后還可以利用傅立葉反變換將這些頻域信號轉(zhuǎn)換成時域信號。
從現(xiàn)代數(shù)學(xué)的眼光來看，傅里葉變換是一種特殊的積分變換。它能將滿足一定條件的某個函數(shù)表示成正弦基函數(shù)的線性組合或者積分。在不同的研究領(lǐng)域，傅里葉變換具有多種不同的變體形式，如連續(xù)傅里葉變換和離散傅里葉變換。
在數(shù)學(xué)領(lǐng)域，盡管最初傅立葉分析是作為熱過程的解析分析的工具，但是其思想方法仍然具有典型的還原論和分析主義的特征。"任意"的函數(shù)通過一定的分解，都能夠表示為正弦函數(shù)的線性組合的形式，而正弦函數(shù)在物理上是被充分研究而相對簡單的函數(shù)類：1. 傅立葉變換是線性算子,若賦予適當?shù)姆稊?shù),它還是酉算子;2. 傅立葉變換的逆變換容易求出,而且形式與正變換非常類似;3. 正弦基函數(shù)是微分運算的本征函數(shù),從而使得線性微分方程的求解可以轉(zhuǎn)化為常系數(shù)的代數(shù)方程的求解.在線性時不變雜的卷積運算為簡單的乘積運算,從而提供了計算卷積的一種簡單手段;5. 離散形式的傅立葉的物理系統(tǒng)內(nèi),頻率是個不變的性質(zhì),從而系統(tǒng)對于復(fù)雜激勵的響應(yīng)可以通過組合其對不同頻率正弦信號的響應(yīng)來獲取;４. 著名的卷積定理指出:傅立葉變換可以化復(fù)變換可以利用數(shù)字計算機快速的算出(其算法稱為快速傅立葉變換算法(FFT))。
正是由于上述的良好性質(zhì),傅里葉變換在物理學(xué)、數(shù)論、組合數(shù)學(xué)、信號處理、概率、統(tǒng)計、密碼學(xué)、聲學(xué)、光學(xué)等領(lǐng)域都有著廣泛的應(yīng)用。
2、圖像傅立葉變換的物理意義
圖像的頻率是表征圖像中灰度變化劇烈程度的指標，是灰度在平面空間上的梯度。如：大面積的沙漠在圖像中是一片灰度變化緩慢的區(qū)域，對應(yīng)的頻率值很低；而對于地表屬性變換劇烈的邊緣區(qū)域在圖像中是一片灰度變化劇烈的區(qū)域，對應(yīng)的頻率值較高。傅立葉變換在實際中有非常明顯的物理意義，設(shè)f是一個能量有限的模擬信號，則其傅立葉變換就表示f的譜。從純粹的數(shù)學(xué)意義上看，傅立葉變換是將一個函數(shù)轉(zhuǎn)換為一系列周期函數(shù)來處理的。從物理效果看，傅立葉變換是將圖像從空間域轉(zhuǎn)換到頻率域，其逆變換是將圖像從頻率域轉(zhuǎn)換到空間域。換句話說，傅立葉變換的物理意義是將圖像的灰度分布函數(shù)變換為圖像的頻率分布函數(shù)，傅立葉逆變換是將圖像的頻率分布函數(shù)變換為灰度分布函數(shù)
傅立葉變換以前，圖像（未壓縮的位圖）是由對在連續(xù)空間（現(xiàn)實空間）上的采樣得到一系列點的集合，我們習(xí)慣用一個二維矩陣表示空間上各點，則圖像可由z=f(x,y)來表示。由于空間是三維的，圖像是二維的，因此空間中物體在另一個維度上的關(guān)系就由梯度來表示，這樣我們可以通過觀察圖像得知物體在三維空間中的對應(yīng)關(guān)系。為什么要提梯度？因為實際上對圖像進行二維傅立葉變換得到頻譜圖，就是圖像梯度的分布圖，當然頻譜圖上的各點與圖像上各點并不存在一一對應(yīng)的關(guān)系，即使在不移頻的情況下也是沒有。傅立葉頻譜圖上我們看到的明暗不一的亮點，實際上圖像上某一點與鄰域點差異的強弱，即梯度的大小，也即該點的頻率的大小（可以這么理解，圖像中的低頻部分指低梯度的點，高頻部分相反）。一般來講，梯度大則該點的亮度強，否則該點亮度弱。這樣通過觀察傅立葉變換后的頻譜圖，也叫功率圖，我們首先就可以看出，圖像的能量分布，如果頻譜圖中暗的點數(shù)更多，那么實際圖像是比較柔和的（因為各點與鄰域差異都不大，梯度相對較小），反之，如果頻譜圖中亮的點數(shù)多，那么實際圖像一定是尖銳的，邊界分明且邊界兩邊像素差異較大的。對頻譜移頻到原點以后，可以看出圖像的頻率分布是以原點為圓心，對稱分布的。將頻譜移頻到圓心除了可以清晰地看出圖像頻率分布以外，還有一個好處，它可以分離出有周期性規(guī)律的干擾信號，比如正弦干擾，一副帶有正弦干擾，移頻到原點的頻譜圖上可以看出除了中心以外還存在以某一點為中心，對稱分布的亮點集合，這個集合就是干擾噪音產(chǎn)生的，這時可以很直觀的通過在該位置放置帶阻濾波器消除干擾
另外我還想說明以下幾點：
1、圖像經(jīng)過二維傅立葉變換后，其變換系數(shù)矩陣表明：
若變換矩陣Fn原點設(shè)在中心，其頻譜能量集中分布在變換系數(shù)短陣的中心附近(圖中陰影區(qū))。若所用的二維傅立葉變換矩陣Fn的原點設(shè)在左上角，那么圖像信號能量將集中在系數(shù)矩陣的四個角上。這是由二維傅立葉變換本身性質(zhì)決定的。同時也表明一股圖像能量集中低頻區(qū)域。
2 、變換之后的圖像在原點平移之前四角是低頻，最亮，平移之后中間部分是低頻，最亮，亮度大說明低頻的能量大（幅角比較大）