在計(jì)算復(fù)雜性里面，如果一個(gè)算法的時(shí)間復(fù)雜度是輸入數(shù)據(jù)的多項(xiàng)式表達(dá)，但卻是輸入長度的指數(shù)時(shí)間算法，那么稱其為偽多項(xiàng)式時(shí)間。

    如果一個(gè)NPC問題存在偽多項(xiàng)式時(shí)間算法，那么稱其為Weakly NP-Complete。否則，稱為Strongly NP-Complete.

   很明顯的一個(gè)例子是0-1背包問題，這一點(diǎn)經(jīng)常容易引起別人的誤解。其實(shí)0-1背包問題是一個(gè)NPC問題，你可以簡單的把它規(guī)約到子集和問題，但是有人經(jīng)常爭辯說0-1 kanpsack問題存在Polynomial Algorithm，那么問題就在這里，那個(gè)所謂的Polynomial Algorithm is Pseudo-Polynomial actually！

   一個(gè)經(jīng)典0-1背包問題的DP解法的時(shí)間復(fù)雜度是O(nW)，W為背包容量，但是背包容量是否需要枚舉[min(…),\sum(…)]呢？所以問題就在這里了復(fù)雜度是O(n2^n)…

   還有一個(gè)問題就是素性檢測！這個(gè)當(dāng)然也是NPC的了。。

    In the case of primality, it turns out there is a different algorithm for testing whether n is prime (discovered in 2002) which runs in time O(log⁶n).

如果仍然不是很清楚，那么需要熟悉一下NPC與P類問題區(qū)別，下面是一個(gè)不錯(cuò)的表格。。。

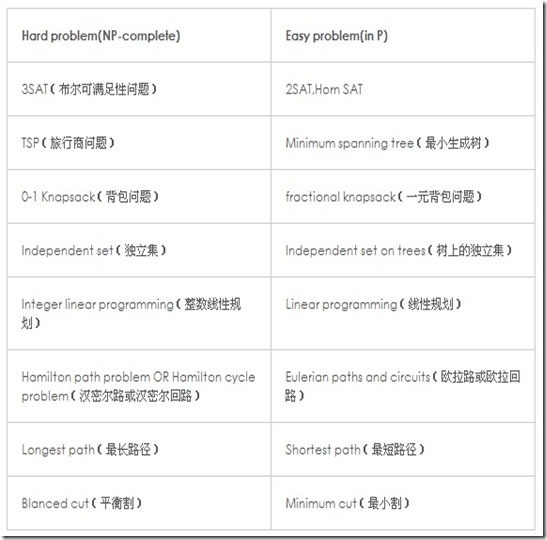
  不過貌似在源blog中有一處錯(cuò)誤。。。Linear Programming的確是P問題，但是解決這個(gè)P問題的simplex 算法卻不是Polynomial的，這個(gè)需要注意！