Cross-validation is a technique for assessing how the results of a statistical analysis will generalize to an independent data set. It is mainly used in settings where the goal is prediction, and one wants to estimate how accurately a predictive model will perform in practice. One round of cross-validation involves partitioning a sample of data into complementary subsets, performing the analysis on one subset (called the training set), and validating the analysis on the other subset (called the validation set or testing set). To reduce variability, multiple rounds of cross-validation are performed using different partitions, and the validation results are averaged over the rounds.
通俗的講，就是為了驗(yàn)證我們得到的模型在實(shí)踐當(dāng)中表現(xiàn)是否準(zhǔn)確！
Purpose of cross validation
我們?yōu)槭裁匆鼋徊骝?yàn)證？交叉驗(yàn)證的目的是什么呢？
Suppose we have a model with one or more unknown parameters, and a data set to which the model can be fit (the training data set). The fitting process optimizes the model parameters to make the model fit the training data as well as possible. If we then take an independent sample of validation data from the same population as the training data, it will generally turn out that the model does not fit the validation data as well as it fits the training data. This is called overfitting, and is particularly likely to happen when the size of the training data set is small, or when the number of parameters in the model is large. Cross-validation is a way to predict the fit of a model to a hypothetical validation set when an explicit validation set is not available.
Common types of cross-validation
交叉驗(yàn)證的通常的種類：
Repeated random sub-sampling validation (通常說(shuō)的Holdout驗(yàn)證)
This method randomly splits the dataset into training and validation data. For each such split, the model is fit to the training data, and predictive accuracy is assessed using the validation data. The results are then averaged over the splits. The advantage of this method (over k-fold cross validation) is that the proportion of the training/validation split is not dependent on the number of iterations (folds). The disadvantage of this method is that some observations may never be selected in the validation subsample, whereas others may be selected more than once. In other words, validation subsets may overlap. This method also exhibits Monte Carlo variation, meaning that the results will vary if the analysis is repeated with different random splits.
In a stratified variant of this approach, the random samples are generated in such a way that the mean response value (i.e. the dependent variable in the regression) is equal in the training and testing sets. This is particularly useful if the responses are dichotomous with an unbalanced representation of the two response values in the data.
隨機(jī)從最初的樣本中選出部分，形成交叉驗(yàn)證數(shù)據(jù)，而剩余的就當(dāng)做訓(xùn)練數(shù)據(jù)。 一般來(lái)說(shuō)，少于原本樣本三分之一的數(shù)據(jù)被選做驗(yàn)證數(shù)據(jù)。
K-fold cross-validation
In K-fold cross-validation, the original sample is randomly partitioned into K subsamples. Of the K subsamples, a single subsample is retained as the validation data for testing the model, and the remainingK ? 1 subsamples are used as training data. The cross-validation process is then repeated K times (thefolds), with each of the K subsamples used exactly once as the validation data. The K results from the folds then can be averaged (or otherwise combined) to produce a single estimation. The advantage of this method over repeated random sub-sampling is that all observations are used for both training and validation, and each observation is used for validation exactly once. 10-fold cross-validation is commonly used [5].
In stratified K-fold cross-validation, the folds are selected so that the mean response value is approximately equal in all the folds. In the case of a dichotomous classification, this means that each fold contains roughly the same proportions of the two types of class labels.
k × 2 cross-validation
This is a variation on k-fold cross-validation. For each fold, we randomly assign data points to two sets d0and d1, so that both sets are equal size (this is usually implemented as shuffling the data array and then splitting in two). We then train on d0 and test on d1, followed by training on d1 and testing on d0.
This has the advantage that our training and test sets are both large, and each data point is used for both training and validation on each fold. In general, k = 5 (resulting in 10 training/validation operations) has been shown to be the optimal value of k for this type of cross-validation[citation needed].
傳統(tǒng)的k折交叉驗(yàn)證的變種！
Leave-one-out cross-validation
As the name suggests, leave-one-out cross-validation (LOOCV) involves using a single observation from the original sample as the validation data, and the remaining observations as the training data. This is repeated such that each observation in the sample is used once as the validation data. This is the same as a K-fold cross-validation with K being equal to the number of observations in the original sample. Leave-one-out cross-validation is usually very expensive from a computational point of view because of the large number of times the training process is repeated.
留一驗(yàn)證，是只留一個(gè)observation來(lái)做驗(yàn)證，其余做訓(xùn)練，缺點(diǎn)當(dāng)然是計(jì)算代價(jià)超級(jí)大！
Measures of fit
The goal of cross-validation is to estimate the expected level of fit of a model to a data set that is independent of the data that were used to train the model. It can be used to estimate any quantitative measure of fit that is appropriate for the data and model. For example, for binary classification problems, each case in the validation set is either predicted correctly or incorrectly. In this situation the misclassification error rate can be used to summarize the fit, although other measures like positive predictive value could also be used. When the value being predicted is continuously distributed, the mean squared error, root mean squared error or median absolute deviation could be used to summarize the errors.
Limitations and misuse
Cross-validation only yields meaningful results if the validation set and test set are drawn from the same population. In many applications of predictive modeling, the structure of the system being studied evolves over time. This can introduce systematic differences between the training and validation sets. For example, if a model for predicting stock values is trained on data for a certain five year period, it is unrealistic to treat the subsequent five year period as a draw from the same population. As another example, suppose a model is developed to predict an individual's risk for being diagnosed with a particular disease within the next year. If the model is trained using data from a study involving only a specific population group (e.g. young people or males), but is then applied to the general population, the cross-validation results from the training set could differ greatly from the actual predictive performance.
If carried out properly, and if the validation set and training set are from the same population, cross-validation is nearly unbiased. However there are many ways that cross-validation can be misused. If it is misused and a true validation study is subsequently performed, the prediction errors in the true validation are likely to be much worse than would be expected based on the results of cross-validation.
These are some ways that cross-validation can be misused:
- By using cross-validation to assess several models, and only stating the results for the model with the best results.
- By performing an initial analysis to identify the most informative features using the entire data set – if feature selection or model tuning is required by the modeling procedure, this must be repeated on every training set. If cross-validation is used to decide which features to use, an inner cross-validation to carry out the feature selection on every training set must be performed.
- By allowing some of the training data to also be included in the test set – this can happen due to "twinning" in the data set, whereby some exactly identical or nearly identical samples are present in the data set.
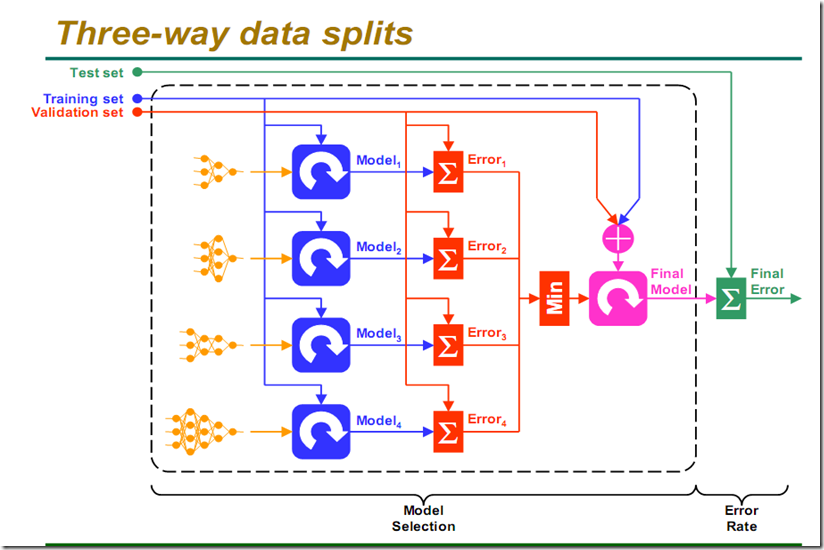
我們首先有不同復(fù)雜度的modle，然后利用training data進(jìn)行訓(xùn)練，利用validation set驗(yàn)證，Error求和，選擇error最小的，最后選擇模型輸出，計(jì)算Final Error！