Dijkstra算法:
普通實現復雜度O(n^2) BinaryHeaps優化的是O(mlogn) Fib堆優化的是O(m+nlogn) m是圖的邊數���,n是圖的點數
特點: 基本思想是貪心思想���,對于每個節點v[i]��,維護估計最短路長度最大值 每次取出一個使得該估計值最小的t,并采用與t相連的邊對其余點的估計值進行更新,更新后不再考慮t�����。在此過程中���,估計值單調遞減���,所以可以得到確切的最短路��。
使用松弛技術���,
優點: 簡單���,實現快速���! 具有貪心算法的特性:最短路徑的子路徑是最短路徑��! 相比于和他同類型的Bellman ford,它更快���,缺點是邊權值非負。
缺點: 邊的權值必須為非負,Dijkstra算法假定輸入圖中的所有邊的權值都是非負的
樸素Dijkstra算法實現:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define INF 329999 //定義此圖的最大距離
#define MaxN 100 //一個圖最大的點數
int cost[MaxN][MaxN]; //此為Dijkstra的數組實現,復雜度為O(n^2)
int pathCon[MaxN]; //記錄最短路徑獲得的時候的前向節點 路徑重建
int pathDis[MaxN]; //路徑距離
int vis[MaxN]; //標記是否結束訪問
void Dijkstra(int n, int root)
{
memset(vis, 0, sizeof(vis)); //標記vis為全部未訪問
vis[root] = 1; //標記root已訪問
for (int i=0; i<n; i++)
pathDis[i] = cost[root][i], pathCon[i] = root;
pathDis[root] = 0; pathCon[root] = -1; // 樹根的標記
int pre = root;
for (int i=1; i<n; i++) //遍歷剩下的n-1個點�����,每執行一次能夠確定一個點的最短距離
{
int Min = INF;
for (int j=0; j<n; j++)
{
if (vis[j]==0 && cost[pre][j]!=INF && pathDis[pre]+cost[pre][j]<pathDis[j])
pathDis[j] = pathDis[pre] + cost[pre][j],pathCon[j] = pre;
}
for (int j=0; j<n; j++)
{
if (vis[j] == 0 && pathDis[j] < Min)
Min = pathDis[j], pre = j;
}
vis[pre] = 1;
}
}
void init(int n) //初始化構建矩陣的時候��,不相鄰元素距離為INF,自身到自身距離為0
{
//n=4
cost[0][0]=0, cost[0][1]=5,cost[0][2]=1, cost[0][3]=4, cost[0][4]=INF;
cost[1][0]=5, cost[1][1]=0,cost[1][2]=3, cost[1][3]=1, cost[1][4]=2;
cost[2][0]=1, cost[2][1]=3,cost[2][2]=0, cost[2][3]=INF,cost[2][4]=6;
cost[3][0]=4, cost[3][1]=1,cost[3][2]=INF,cost[3][3]=0, cost[3][4]=3;
cost[4][0]=INF,cost[4][1]=2,cost[4][2]=6, cost[4][3]=3, cost[4][4]=0;
}
void reshape(int n,int root)
{
for(int i=0;i<n;i++)
{
if(pathDis[i]==INF) cout<<"node "<<root<<" to node "<<i<<"is INF"<<endl;
else cout<<"node "<<root<<" to node "<<i<<"is "<<pathDis[i]<<endl;
}
vector<int> Path[MaxN]; //構建每條最短路徑
for(int i=n-1;i>=0;i--)
{
vector<int> temp;
int j=i;temp.push_back(j);
while(pathCon[j]!=-1)
{
temp.push_back(pathCon[j]);
j=pathCon[j];
}
reverse(temp.begin(),temp.end());
Path[i]=temp;
}
for(int i=0;i<n;i++)
{
cout<<"Path "<<root<<" "<<"to "<<i<<" is ";
for(int j=0;j<Path[i].size();j++)
cout<<Path[i][j]<<" ";
cout<<endl;
}
}
int main() //n個點�����,所以n是5
{
init(5);
Dijkstra(5,0);
reshape(5,0);
}
加入優先隊列優化的Dijkstra算法:
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
// Dijkstra O(m*log n)
#define MaxN 100 //一個圖最大的點數
#define MaxM 1000 //一個圖最大的邊數
#define V MaxN
#define E MaxM
#define INF 329999 //定義此圖的最大距離
#define typec int // type of cost
typec cost[E], pathDis[V]; // cost[E] 每條邊的代價 pathDis[V]最短路徑的值
int e, pnt[E], cluster[E], head[V];
int pathCon[V], vis[V];
/*
pnt[] 保存每條邊的終點
cost[] 保存每條邊的權值
cluster[] 把邊按照起始點聚類
head[u] u號節點的邊結束邊序號
*/
struct qnode {
int v; typec c;
qnode (int vv = 0, typec cc = 0) : v(vv), c(cc) {}
bool operator < (const qnode& r) const { return c>r.c; }
};
void dijkstra(int n, const int root)
{
qnode mv;
priority_queue<qnode> que;
vis[root] = 1; pathDis[root] = 0;
que.push(qnode(root, 0));
for (int pre = root, i=1; i<n; i++) //循環n次
{
for (int j = head[pre]; j != -1; j = cluster[j]) //展開節點
{
int k = pnt[j]; //j為邊索引號
if (vis[k] == 0 &&
pathDis[pre] + cost[j] < pathDis[k])
{
pathDis[k] = pathDis[pre] + cost[j];
que.push(qnode(pnt[j], pathDis[k]));
pathCon[k] = pre;
}
}
while (!que.empty() && vis[que.top().v] == 1)
que.pop();
if (que.empty()) break;
mv = que.top(); que.pop();
vis[pre = mv.v] = 1;
}
}
inline void addedge(int u, int v, typec c){
pnt[e] = v; cost[e] = c; cluster[e] = head[u]; head[u] = e++;
}
void init(int n, int m) //n為點數, m 為邊數
{
int i, u, v; typec c;
e = 0;
memset(head, -1, sizeof(head));
memset(vis, 0, sizeof(vis));
memset(pathCon, -1, sizeof(pathCon));
for (i = 0; i < n; i++) pathDis[i] = INF;
//for (i = 0; i < n; ++i)
//{
//scanf("%d%d%d", &u, &v, &c); // %d: type of cost
//addedge(u, v, c); // 這里添加的是單向邊,如果題目描述不同��,需要加入addedge(v,u,c);
//}
addedge(0,2,1);
addedge(2,0,1);
addedge(0,1,4);
addedge(1,0,4);
addedge(1,3,1);
addedge(3,1,1);
addedge(2,3,4);
addedge(3,2,4);
addedge(2,4,2);
addedge(4,2,2);
addedge(3,5,2);
addedge(6,3,2);
addedge(4,5,3);
addedge(5,4,3);
}
void reshape(int n,int root)
{
for(int i=0;i<n;i++)
{
if(pathDis[i]==INF) cout<<"node "<<root<<" to node "<<i<<"is INF"<<endl;
else cout<<"node "<<root<<" to node "<<i<<"is "<<pathDis[i]<<endl;
}
vector<int> Path[MaxN]; //構建每條最短路徑
for(int i=n-1;i>=0;i--)
{
vector<int> temp;
int j=i;temp.push_back(j);
while(pathCon[j]!=-1)
{
temp.push_back(pathCon[j]);
j=pathCon[j];
}
reverse(temp.begin(),temp.end());
Path[i]=temp;
}
for(int i=0;i<n;i++)
{
cout<<"Path "<<root<<" "<<"to "<<i<<" is ";
for(int j=0;j<Path[i].size();j++)
cout<<Path[i][j]<<" ";
cout<<endl;
}
}
int main()
{
init(6,7); //n = 6 m = 7
dijkstra(6, 3);
reshape(6,3);
}
上述實現的圖是:
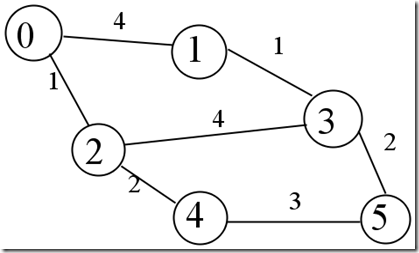
用LatexDraw 畫的圖��,效果還可以�����。。���。