貝葉斯統計與頻率統計
先驗分布 它是總體分布參數θ的一個概率分布����。貝葉斯學派的根本觀點����,是認為在關于θ的任何統計推斷問題中,除了使用樣本X所提供的信息外,還必須對θ規定一個先驗分布,它是在進行推斷時不可或缺的一個要素����。貝葉斯學派把先驗分布解釋為在抽樣前就有的關于θ的先驗信息的概率表述����,先驗分布不必有客觀的依據����,它可以部分地或完全地基于主觀信念。例如,某甲懷疑自己患有一種疾病A,在就診時醫生對他測了諸如體溫、血壓等指標,其結果構成樣本X����。引進參數θ:有病時,θ=1;無病時,θ=0。X的分布取決于θ是0還是1,因而知道了X有助于推斷θ是否為1。按傳統(頻率)學派的觀點,醫生診斷時,只使用X提供的信息;而按貝葉斯學派觀點,則認為只有在規定了一個介于0與1之間的數p作為事件{θ=1}的先驗概率時����,才能對甲是否有?���。?i>θ是否為1)進行推斷����。p這個數刻畫了本問題的先驗分布,且可解釋為疾病A的發病率。先驗分布的規定對推斷結果有影響����,如在此例中����,若疾病A的發病率很小,醫生將傾向于只有在樣本X顯示出很強的證據時,才診斷甲有病����。在這里先驗分布的使用看來是合理的,但貝葉斯學派并不是基于 “p是發病率”這樣一個解釋而使用它的����,事實上即使對本病的發病率毫無所知����,也必須規定這樣一個p����,否則問題就無法求解����。
后驗分布 根據樣本 X 的分布Pθ及θ的先驗分布π(θ),用概率論中求條件概率分布的方法,可算出在已知X=x的條件下,θ的條件分布 π(θ|x)����。因為這個分布是在抽樣以后才得到的����,故稱為后驗分布����。貝葉斯學派認為:這個分布綜合了樣本X及先驗分布π(θ)所提供的有關的信息。抽樣的全部目的����,就在于完成由先驗分布到后驗分布的轉換����。如上例,設p=P(θ=1)=0.001,而π(θ=1|x)=0.86,則貝葉斯學派解釋為:在某甲的指標量出之前,他患病的可能性定為0.001����,而在得到X后,認識發生了變化:其患病的可能性提高為0.86,這一點的實現既與X有關,也離不開先驗分布����。
先驗概率 由以往的數據分析得到的概率
后驗概率 得到信息之后����,再重新加以修正的概率
貝葉斯定理 這個是廣為人知的常識
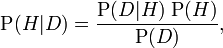
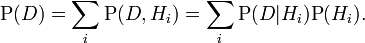
所以,Bayes` theorem was used to convert a prior probability into a posterior probability!
我們給出一個似然(likelihood)的定義����,我們可以把貝葉斯定理用下面的word來闡釋:
posterior 正比于 likehood * prior
上述有所的這些值都可以看成是先驗概率的函數! P(D)僅僅是一個歸一化的常量����!
將貝葉斯公式兩邊積分得到:(先驗概率的表示不同����,上面寫成了H,現在寫成了w)
 上面有這個式子的離散化表述����!
上面有這個式子的離散化表述����!
我們平時所說的最大似然估計,就是最大化我們的似然函數 p(D|w) (P(D|H))
那么頻率統計和貝葉斯統計的區別在哪里����? 先驗分布問題����!
關于貝葉斯方法的爭論 貝葉斯學派與頻率學派爭論的焦點在于先驗分布的問題����。所謂頻率學派是指堅持概率的頻率解釋的統計學家形成的學派。貝葉斯學派認為先驗分布可以是主觀的,它沒有也不需要有頻率解釋����。而頻率學派則認為����,只有在先驗分布有一種不依賴主觀的意義����,且能根據適當的理論或以往的經驗決定時,才允許在統計推斷中使用先驗分布����,否則就會喪失客觀性。另一個批評是:貝葉斯方法對任何統計問題都給以一種程式化的解法,這導致人們對問題不去作深入分析����,而只是機械地套用公式����。貝葉斯學派則認為:從理論上說����,可以在一定條件下證明,任何合理的優良性準則必然是相應于一定先驗分布的貝葉斯準則����,因此每個統計學家自覺或不自覺地都是“貝葉斯主義者”����。他們認為����,頻率學派表面上不使用先驗分布,但所得到的解也還是某種先驗分布下的貝葉斯解,而這一潛在的先驗分布,可能比經過慎重選定的主觀先驗分布更不合理����。其次����,貝葉斯學派還認為����,貝葉斯方法對統計推斷和決策問題給出程式化的解是優點而非缺點����,因為它免除了尋求抽樣分布����,(見統計量)這個困難的數學問題����。而且這種程式化的解法并不是機械地套公式,它要求人們對先驗分布����、損失函數等的選擇作大量的工作����。還有����,貝葉斯學派認為,用貝葉斯方法求出的解不需要頻率解釋,因而即使在一次使用下也有意義。反之,根據概率的頻率解釋而提供的解,則只有在大量次數使用之下才有意義,而這常常不符合應用的實際����。這兩個學派的爭論是戰后數理統計學發展中的一個特色����。這個爭論目前還遠沒有解決����,它對今后數理統計學的發展還將產生影響。
在我們平常使用的貝葉斯定理中����,關于先驗概率一般都是像:對以往數據分析結果表明����。����。����。。����。根據以往的臨床記錄����。����。。����。����。之類的����。。