Two analytical 2d line intersection in OpenCASCADE
eryar@163.com
Abstract. OpenCASCADE geometric tools provide algorithms to calculate the intersection of two 2d curves, surfaces, or a 3d curve and a surface. Those are the basis of the Boolean Operation, so under the implementation can help to under the BO algorithms. The paper focus on the intersection of two 2d analytical line.
Key Words. OpenCASCADE, Line Intersection
1.Introduction
在幾何造型系統(tǒng)中,通常利用集合的并、交、差運算實現(xiàn)復(fù)雜形體的構(gòu)造,而集合運算需要大量的求交運算。如何提高求交的實用性、穩(wěn)定性、速度和精度等,對幾何造型系統(tǒng)至關(guān)重要。當前的幾何造型系統(tǒng),大多數(shù)采用邊界表示法來表示模型。在這種表示法中,形體的邊界元素和某類幾何元素相對應(yīng),它們可以是直線、圓弧、二次曲線、Bezier曲線和B樣條曲線等,也可以是平面、球面、二次曲面、Bezier曲面和B樣條曲面等,求交情況十分復(fù)雜。在一個典型的幾何造型系統(tǒng)中,用到的幾何元素通常有25種,為了建立一個通用的求交函數(shù)庫,所要完成的求交函數(shù)多達:

在OpenCASCADE中也有類似的數(shù)據(jù)結(jié)構(gòu)來表示幾何體。本文先來學(xué)習(xí)最簡單的一種求交:兩條二維直線的相交。
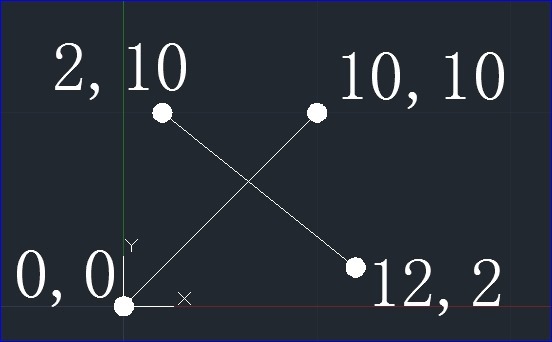
Figure 1. 2d line intersection
2.Code Usage
OpenCASCADE中計算二維解析曲線的類是IntAna2d_AnaIntersection,可用于計算如下的曲線之間的相交:
v 兩條二維直線;
v 兩個二維圓;
v 二維直線和二維圓;
v 二維直線、圓、橢圓、拋物線、雙曲線二次曲線與另外一條二維曲線;
下面使用OpenCASCADE來對圖1所示的兩條二維直線進行求交計算。代碼如下:
/*
Copyright(C) 2017 Shing Liu(eryar@163.com)
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files(the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and / or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions :
The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT.IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
*/
// NOTE
// ----
// Tool: Visual Studio 2013 & OpenCASCADE7.1.0
// Date: 2017-02-25 20:52
#include <gp_Dir2d.hxx>
#include <gp_Lin2d.hxx>
#include <gp_Pnt2d.hxx>
#include <GCE2d_MakeLine.hxx>
#include <IntAna2d_AnaIntersection.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKG2d.lib")
#pragma comment(lib, "TKG3d.lib")
#pragma comment(lib, "TKGeomBase.lib")
void test(void)
{
GCE2d_MakeLine aLineMaker1(gp_Pnt2d(0.0, 0.0), gp_Pnt2d(10.0, 10.0));
GCE2d_MakeLine aLineMaker2(gp_Pnt2d(2.0, 10.0), gp_Pnt2d(12.0, 2.0));
gp_Lin2d aLine1 = aLineMaker1.Value()->Lin2d();
gp_Lin2d aLine2 = aLineMaker2.Value()->Lin2d();
IntAna2d_AnaIntersection aIntAna;
aIntAna.Perform(aLine1, aLine2);
if (aIntAna.IsDone())
{
const IntAna2d_IntPoint& aIntPoint = aIntAna.Point(1);
std::cout << "Number of IntPoint between the 2 curves: "
<< aIntAna.NbPoints() << std::endl;
std::cout << "Intersect Point: " << aIntPoint.Value().X()
<< ", " << aIntPoint.Value().Y() << std::endl;
}
}
int main(int argc, char* argv[])
{
test();
return 0;
}
計算得到交點為(6.44, 6.44):
Number of IntPoint between the 2 curves: 1
Intersect Point: 6.44444, 6.44444
Press any key to continue . . .
3.Code Analysis
計算二維直線相交的代碼在文件IntAna2d_AnaIntersection_1.cxx中,其中名字IntAna2d的意思是Intersection Analytical兩個單詞前三個字母,即二維解析曲線求交包。源碼列出如下:
void IntAna2d_AnaIntersection::Perform (const gp_Lin2d& L1,
const gp_Lin2d& L2) {
done = Standard_False;
Standard_Real A1,B1,C1;
Standard_Real A2,B2,C2;
L1.Coefficients(A1,B1,C1);
L2.Coefficients(A2,B2,C2);
Standard_Real al1,be1,ga1;
Standard_Real al2,be2,ga2;
Standard_Real Det =Max (Abs(A1),Max(Abs(A2),Max(Abs(B1),Abs(B2))));
if (Abs(A1)==Det) {
al1=A1;
be1=B1;
ga1=C1;
al2=A2;
be2=B2;
ga2=C2;
}
else if (Abs(B1)==Det) {
al1=B1;
be1=A1;
ga1=C1;
al2=B2;
be2=A2;
ga2=C2;
}
else if (Abs(A2)==Det) {
al1=A2;
be1=B2;
ga1=C2;
al2=A1;
be2=B1;
ga2=C1;
}
else {
al1=B2;
be1=A2;
ga1=C2;
al2=B1;
be2=A1;
ga2=C1;
}
Standard_Real rap=al2/al1;
Standard_Real denom=be2-rap*be1;
if (Abs(denom)<=RealEpsilon()) { // Directions confondues
para=Standard_True;
nbp=0;
if (Abs(ga2-rap*ga1)<=RealEpsilon()) { // Droites confondues
iden=Standard_True;
empt=Standard_False;
}
else { // Droites paralleles
iden=Standard_False;
empt=Standard_True;
}
}
else {
para=Standard_False;
iden=Standard_False;
empt=Standard_False;
nbp=1;
Standard_Real XS = (be1*ga2/al1-be2*ga1/al1)/denom;
Standard_Real YS = (rap*ga1-ga2)/denom;
if (((Abs(A1)!=Det)&&(Abs(B1)==Det))||
((Abs(A1)!=Det)&&(Abs(B1)!=Det)&&(Abs(A2)!=Det))) {
Standard_Real temp=XS;
XS=YS;
YS=temp;
}
Standard_Real La,Mu;
if (Abs(A1)>=Abs(B1)) {
La=(YS-L1.Location().Y())/A1;
}
else {
La=(L1.Location().X()-XS)/B1;
}
if (Abs(A2)>=Abs(B2)) {
Mu=(YS-L2.Location().Y())/A2;
}
else {
Mu=(L2.Location().X()-XS)/B2;
}
lpnt[0].SetValue(XS,YS,La,Mu);
}
done=Standard_True;
}
從上述源碼中可以看出,OpenCASCADE對二維直線求交計算使用的是解方程組的方法。步驟如下:
v 計算兩條直線的系數(shù);
v 計算系數(shù)方程組。
這些都是高中數(shù)學(xué)知識了,就當復(fù)習(xí)下,并由此看出OpenCASCADE中的一些編碼風格。先看第一步,根據(jù)點和方向計算二維直線的系數(shù),相關(guān)的源碼如下所示:
inline void gp_Lin2d::Coefficients (Standard_Real& A,
Standard_Real& B,
Standard_Real& C) const
{
A = pos.Direction().Y();
B = - pos.Direction().X();
C = -(A * pos.Location().X() + B * pos.Location().Y());
}
由高中數(shù)學(xué)可知,二維直線的方程有三種形式:點斜式、兩點式和一般式。
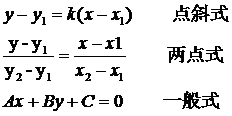
根據(jù)一般式方程,當B不等于0時,可得:
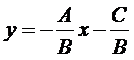
因為OpenCASCADE中的gp_Dir2d是單位向量,所以可將其X、Y值分別對應(yīng)-B和A。確定A和B后,再根據(jù)一般式方程將C移項得到:C=-Ax-By
得到直線的系數(shù)后,交點的計算就變成如下方程組的求解了:
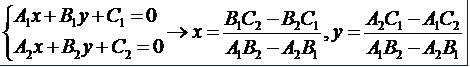
OpenCASCADE的源碼中有多個條件判斷,相當于高期消元法中的選主元操作,主要是為了避免分母為0的情況。其中有兩個實數(shù)直接判斷相等的語句,如Abs(A1)==Det這種。對于實數(shù)大小的比較,一般總是使用兩者相減的值是否落在0的領(lǐng)域中來判斷。OpenCASCADE中對于實數(shù)的比較沒有采用領(lǐng)域比較技術(shù),顯得不夠嚴謹。其實領(lǐng)域比較的方法已經(jīng)在Precison.hxx中進行了說明,只是有些代碼沒有嚴格執(zhí)行。
4.Conclusion
通過對OpenCASCADE中二維直線相交代碼的分析,理解其實現(xiàn)原理:將點向式的直線轉(zhuǎn)換成一般式,再對一般式聯(lián)立方程求解。求解過程中使用了高期消元法的選主元方法。
對于實數(shù)的比較應(yīng)該盡量采用領(lǐng)域比較技術(shù),而避免直接使用兩個數(shù)相等==或不相等!=的判斷。
如果只是判斷兩條直線是否相交,而不用計算交點的話,《算法導(dǎo)論》中有使用向量來高效算法。
因為二維直線相交只涉及到高中數(shù)學(xué)知識,所以本文是拋磚引玉,通過繼續(xù)學(xué)習(xí),理解B樣條曲線的相交算法實現(xiàn)。
5.References
1. 孫家廣, 胡事民. 計算機圖形學(xué)基礎(chǔ). 清華大學(xué)出版社. 2009
2. 人民教育出版社中學(xué)數(shù)學(xué)室. 數(shù)學(xué)第二冊上. 人民教育出版社. 2000
3. 錢能. C++程序設(shè)計教程. 清華大學(xué)出版社. 2005
4. 易大義, 沈云寶, 李有法. 計算方法. 浙江大學(xué)出版社. 2002
5. 潘金貴等譯. 算法導(dǎo)論. 機械工業(yè)出版社. 2011