Posted on 2023-12-02 12:20
eryar 閱讀(1886)
評論(0) 編輯 收藏 引用 所屬分類:
2.OpenCASCADE

OpenCASCADE 曲線求交
eryar@163.com
1 Introduction
OpenCASCADE中提供了二維幾何曲線的求交類Geom2dAPI_InterCurveCurve,對應到三維幾何只提供了GeomAPI_IntCS, GeomAPI_IntSS,沒有提供幾何的GeomAPI_IntCC求交類。這些幾何求交一般使用的是數值算法,即解方程。對于兩條幾何曲線P(u1), Q(u2),求交就是解P(u1) - Q(u2) = 0這個方程。為什么對于三維幾何曲線沒有提供數值算法?
對于拓樸邊提供了求交算法IntTools_EdgeEdge,這個類是使用類似于曲面求交的離散網格法,使用了離散包圍盒法。

基于包圍合盒的算法是個遞歸算法,算法思路:
- 1) 檢查兩條邊在參數范圍內的包圍盒,若空間干涉,則進行下一步;否則退出本次判斷;
- 2) 找出兩條邊包圍盒的公共部分對應的參數,若沒找到,則退出本次判斷;
- 3) 并將第一條邊在參數范圍內分割成2或3部分,執行第一步;
- 4) 退出條件:沒有相交或找到相交的參數值;
第一次是分別分成2部分:
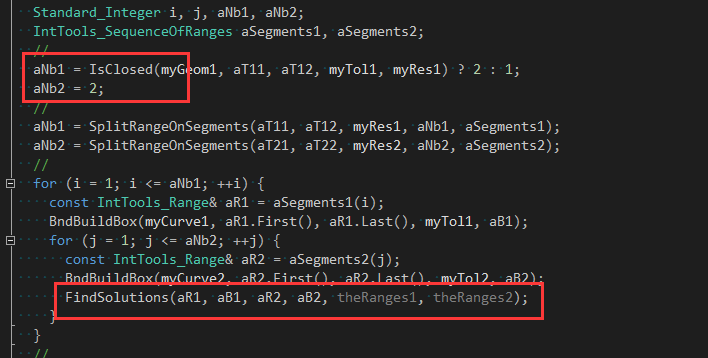
在遞歸函數FindSolutions()中,只去對第一條邊進行參數分割成3部分:
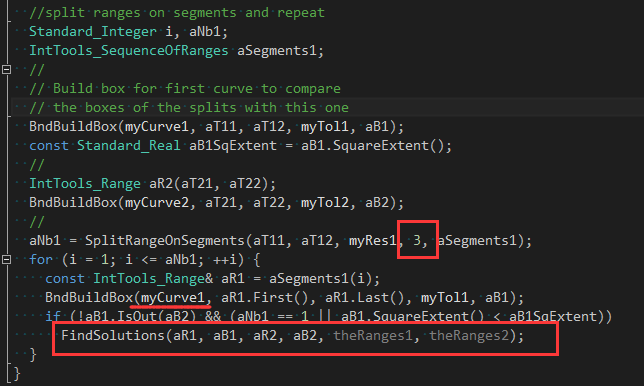
2 輔助函數
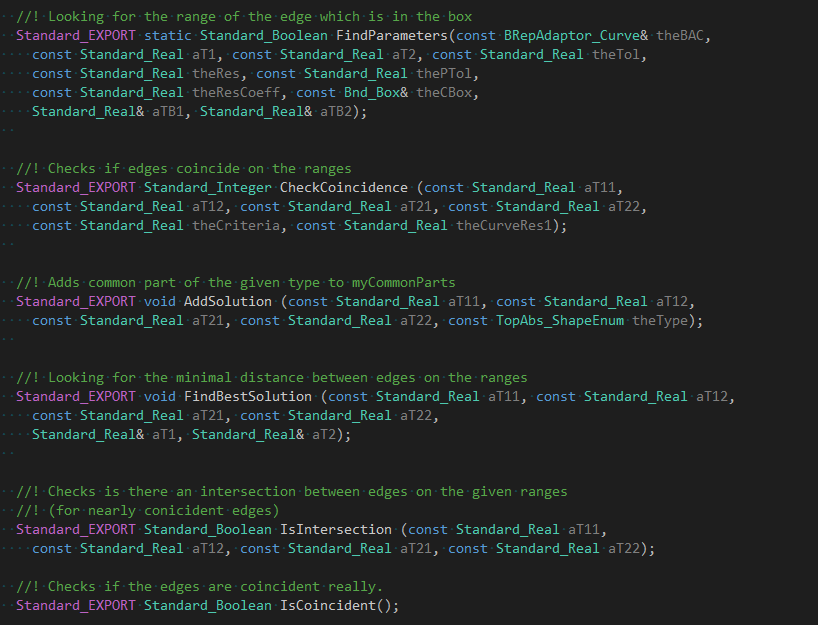
第一個輔助函數是FindParameters(),用來更新第二條邊在第一條邊的的包圍盒中的參數范圍,使用這個參數范圍更新包圍盒。
第二個輔助函數是CheckCoincidence(),用來檢測兩段邊是否重合。第一步是快速計算,對邊采樣10個點,若通過初步粗檢測,后面再深入計算。這些算法都不太高效。
第三個輔助函數是IsIntersection()用來判斷兩邊條在參數范圍內是否相交。
3 測試
將兩條邊求交過程中的包圍盒顯示出來,方便查看理解算法。先測試兩個圓之間的相交:
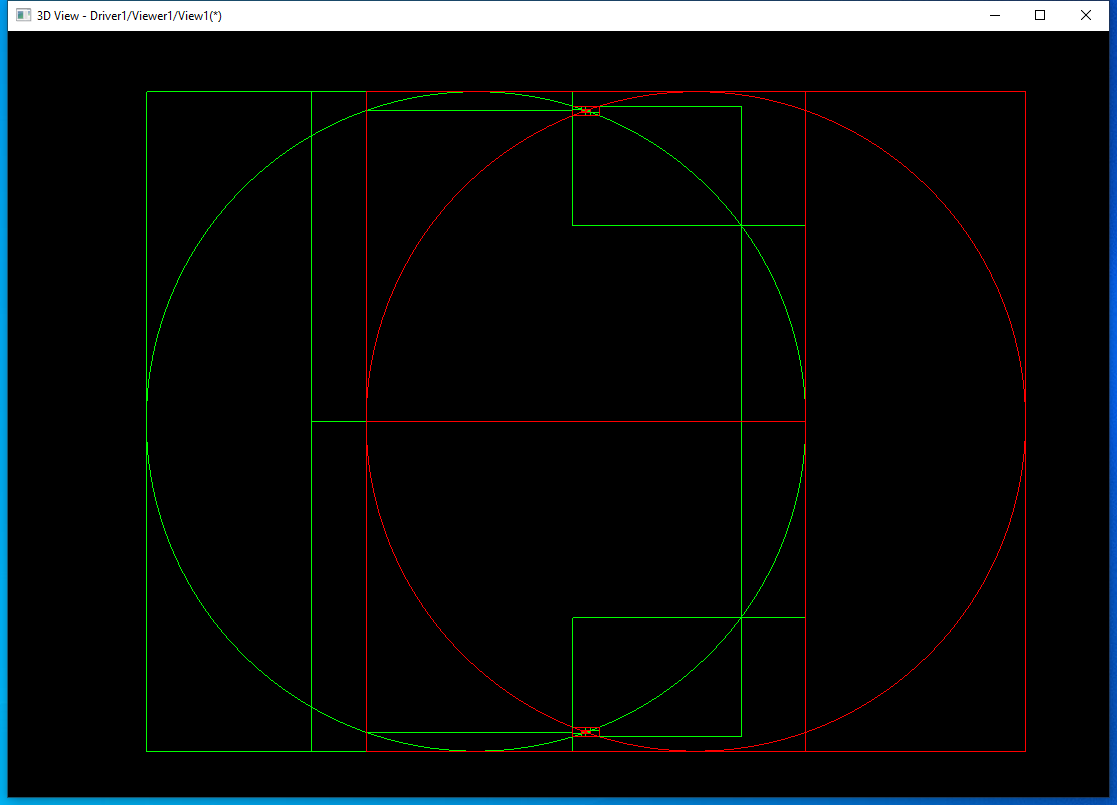
其中第一條邊是綠色的圓,求交過程中的包圍盒也用綠色表示;第二條邊是紅色的圓,求交過程中的包圍盒也用紅色表示。因為圓是閉合的,第一次都分割成2部分。將上面交點處理放大:
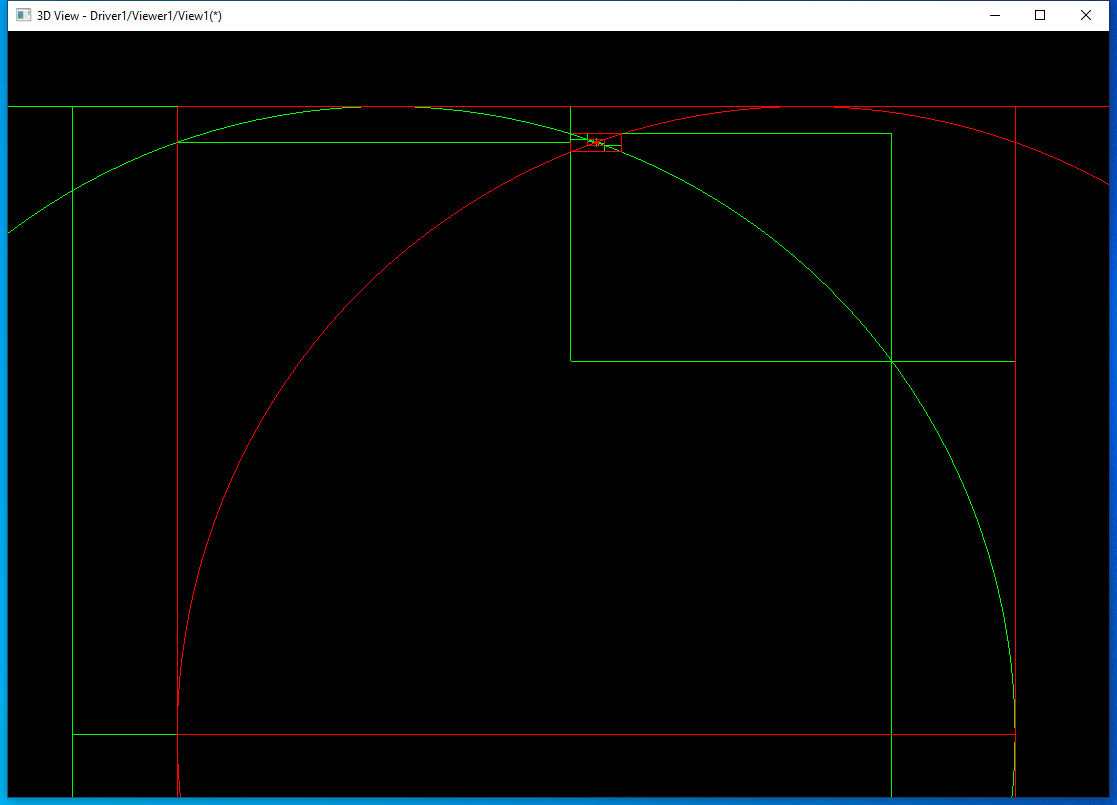
后面都是將第一條邊分割成3部分,然后分別用這3部分的包圍盒去找與第二條邊相交的參數范圍,再更新第二條邊的包圍盒。繼續放大上面交點處:
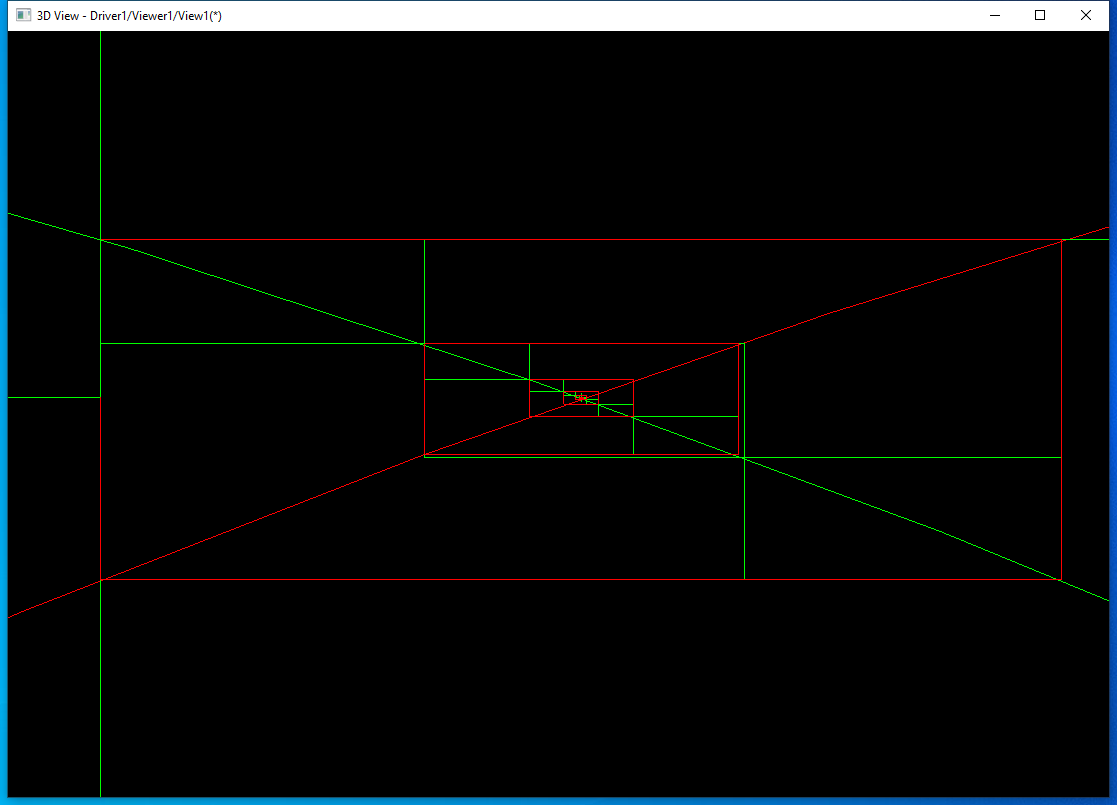
發現對于兩個圓的求交,執行了100次,效率不高。又用兩個B樣條曲線求交來測試:
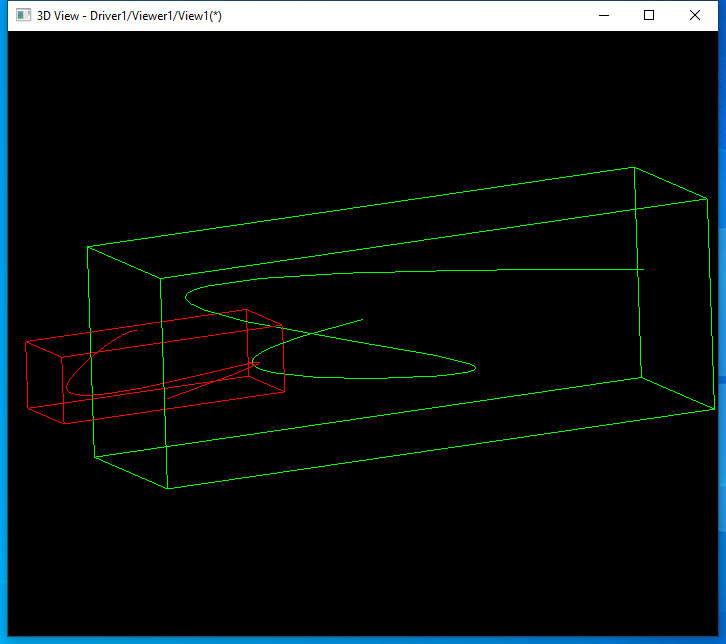
發現對于B樣條曲線求交速度較快。
4 Conclusion
曲線求交需要考慮重合部分,opencascae中沒有使用數值算法來計算,而是采用基于包圍盒的算法來處理。這種算法一般情況下可以快速找到求交解,有時遞歸較深,對于基本曲線可以像曲面求交一樣分類處理以提高性能。opencascade中對于三維曲線求交算法性能還有優化空間。