Representation Data in OpenCascade BRep

eryar@163.com

摘要Abstract：現(xiàn)在的顯示器大多數(shù)是光柵顯示器，即可以看做一個(gè)像素的矩陣。在光柵顯示器上顯示的任何圖形，實(shí)際上都是一些具有一種或多種顏色的集合。數(shù)學(xué)上精確表示的圖形在顯示器中只能用逼近的方式顯示出來(lái)。本文主要對(duì)OpenCascade的BRep文件中用來(lái)顯示曲線和曲面的離散數(shù)據(jù)結(jié)構(gòu)進(jìn)行說(shuō)明。

關(guān)鍵字：OpenCascade, BRep, Polygon, Triangulation, Subdivision Curves,

一、引言 Introduction

光柵圖形顯示器可以看做一個(gè)像素矩陣。在光柵顯示器上顯示的任何一種圖形，實(shí)際上都是一些具有一種或多種顏色的像素的集合。在數(shù)學(xué)上，理想的曲線是沒(méi)有寬度的，它是由無(wú)數(shù)個(gè)點(diǎn)構(gòu)成的集合，而當(dāng)要顯示曲線時(shí)，就不能用無(wú)數(shù)個(gè)點(diǎn)在顯示器中顯示，必須對(duì)其進(jìn)行離散化，即細(xì)分處理。考慮性能要求，需要用盡可能少的點(diǎn)來(lái)顯示曲線。對(duì)于曲面也是一樣，雖然已經(jīng)有曲面的數(shù)學(xué)解析表示，但是需要在顯示器中顯示時(shí)，必須對(duì)其離散化，即三角剖分得到的逼近曲面的三角網(wǎng)格。

在OpenCascade中已經(jīng)有曲線和曲面的精確的數(shù)學(xué)解析表達(dá)形式的類，如下圖所示：

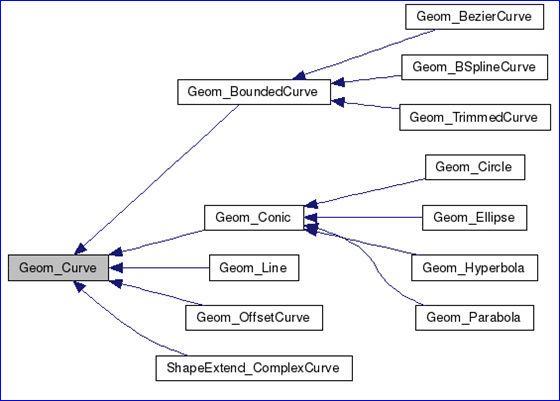
Figure 1.1 Parametric geometry curves

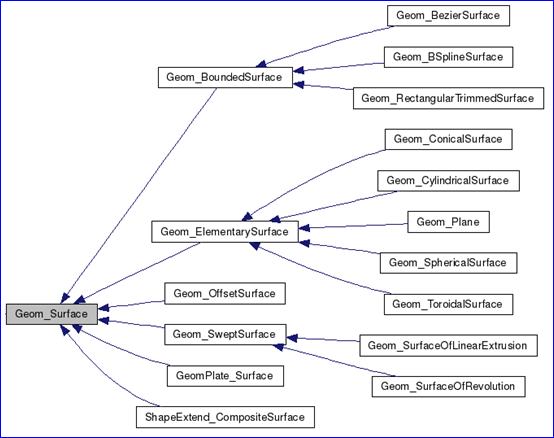
Figure 1.2 Parametric geometry surfaces

在OpenGL中顯示這些曲線和曲面時(shí)，不能直接顯示出由參數(shù)方程精確表示的曲線和曲面，必須對(duì)曲線和曲面進(jìn)行細(xì)分，即離散化，得到OpenGL顯示用的點(diǎn)和三角網(wǎng)格。

在OpenCascade中使用類Poly_Polygon3D/Poly_Polygon2D來(lái)保存多段線的數(shù)據(jù)，即可以用來(lái)保存逼近顯示由參數(shù)方程精確表示的曲線的離散點(diǎn)數(shù)據(jù)。

在OpenCascade中使用類Poly_Triangulation來(lái)保存網(wǎng)格數(shù)據(jù)，即用三角網(wǎng)格來(lái)逼近表示的曲面，或更通用的一個(gè)形狀。

形狀的離散化由函數(shù)BRepMesh::Mesh()來(lái)統(tǒng)一處理，處理后就可以得到形狀用來(lái)顯示的多段線和三角網(wǎng)格數(shù)據(jù)。有了這些離散數(shù)據(jù)，不管是將形狀交給顯示模塊進(jìn)行顯示，還是將形狀在其他顯示引擎中顯示，就很方便了。

在OpenCascade的BRep中也保存了形狀的用來(lái)顯示用的離散數(shù)據(jù)，即多段線和三角網(wǎng)格。只有經(jīng)過(guò)BRepMesh::Mesh()離散化之后，形狀才具有這些數(shù)據(jù)。

二、細(xì)分曲線 Subdivision of Curves

在前面的一篇文章《在OpenSceneGraph中繪制OpenCascade的曲線 》中對(duì)曲線的顯示使用了統(tǒng)一細(xì)分處理（uniform subdivision），即將曲線在整個(gè)參數(shù)區(qū)域內(nèi)均分后得到一些線段來(lái)顯示。沒(méi)有考慮這樣的問(wèn)題：在曲線很平的區(qū)域內(nèi)，就會(huì)存在冗余的點(diǎn)；在曲線曲度很大的區(qū)域內(nèi)，可能點(diǎn)的數(shù)量還不足以顯示出光滑的曲線。自適應(yīng)細(xì)分（Adaptive Subdivision）的方法就是將點(diǎn)放在最需要的地方，其主要目的是可視化曲線時(shí)更高效的渲染。通常這種方法主要用于游戲，因?yàn)槠滹@示更高效，性能更好。

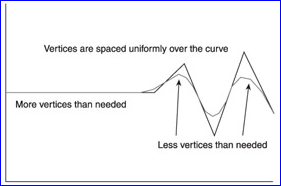
Figure 2.1 Uniform sampling on a curve

如上圖所示，統(tǒng)一采樣來(lái)繪制曲線時(shí)，通常會(huì)在直線段區(qū)域生成很多多余的點(diǎn)，而在曲線區(qū)域的點(diǎn)太少，不能表示出光滑的曲線。自適應(yīng)細(xì)分曲線有很多種方法，每種方法都會(huì)考慮速度、效率和精度，即如何用最少的點(diǎn)精確地表示出曲線。當(dāng)你理解這個(gè)基本概念后，也可以對(duì)其他方法進(jìn)行研究。

在OpenCascade中對(duì)曲線的細(xì)分使用的類是GCPnts_TangentialDeflection，其算法描述如下，感興趣的讀者可以結(jié)合源程序?qū)ζ渌惴▽?shí)現(xiàn)進(jìn)行研究：

其中各個(gè)點(diǎn)的橫坐標(biāo)對(duì)應(yīng)的參數(shù)分別為：

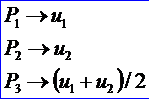
從上述公式結(jié)合向量的數(shù)量積公式可以看出，約束條件是兩個(gè)向量夾角的余弦值分別小于角度偏差和曲率偏差。算法將產(chǎn)生滿足約束條件的曲線上的最少數(shù)量的點(diǎn)。

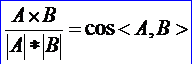
細(xì)分曲線后的點(diǎn)保存在類Poly_Polygon3D中。在BRep中也保存有多段線數(shù)據(jù)，如下所示：

示例：

BNF定義：

詳細(xì)說(shuō)明：

<3D polygon record>定義了空間多段線（3D polyline）L，用來(lái)逼近空間參數(shù)曲線C。多段線的數(shù)據(jù)包含節(jié)點(diǎn)數(shù)m>=2，參數(shù)顯示標(biāo)志位p，逼近偏差（deflection）d>=0，節(jié)點(diǎn)Ni（1=<i<=m），參數(shù)ui（1=<i<=m）。當(dāng)參數(shù)顯示標(biāo)志位p＝1時(shí)，參數(shù)u才會(huì)顯示。多段線L通過(guò)這些節(jié)點(diǎn)，多段線L逼近曲線C的逼近偏差定義如下所示：

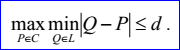
參數(shù)ui（1=<i<=m）是曲線C上通過(guò)節(jié)點(diǎn)Ni的參數(shù)值：

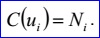
示例數(shù)據(jù)表示的多段線為：m＝2，參數(shù)顯示標(biāo)志位p＝1，逼近偏差d＝0.1，節(jié)點(diǎn)N1＝（1，0，0），N2＝（2，0，0），參數(shù)u1＝0，u2＝1。

三、細(xì)分曲面 Subdivision of surfaces

我們知道使用參數(shù)方程可以精確表示出三維曲線和曲面，但是參數(shù)方程表示的曲線曲面并不能直接交給OpenGL直接顯示出來(lái)。為此，圖形學(xué)中廣泛使用三角網(wǎng)格來(lái)表達(dá)三維模型，即用三角形組成的面片列表來(lái)近似逼近表示三維模型。

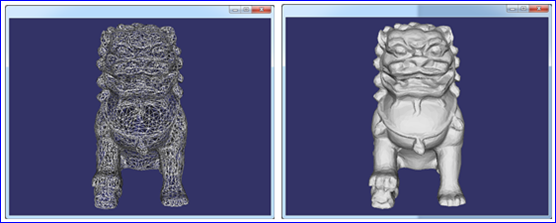
Figure 3.1 Triangulation of Chinese Dragon

用三角網(wǎng)格表示的曲面需要解決幾個(gè)問(wèn)題：三角網(wǎng)格的產(chǎn)生、描述、遍歷、簡(jiǎn)化和壓縮等。在OpenCascade中三角網(wǎng)格的產(chǎn)生使用算法Delaunay三角剖分算法生成網(wǎng)格數(shù)據(jù)，網(wǎng)格的描述使用類Poly_Triangulation。BRep文件中也保存三角網(wǎng)格的數(shù)據(jù)，如下所示：

示例：

BNF定義：

詳細(xì)說(shuō)明：

<triangulation record>定義了逼近曲面S的三角剖分T（triangulation）。三角剖分的數(shù)據(jù)包含節(jié)點(diǎn)數(shù)m>=3，三角形數(shù)k>=1，參數(shù)顯示標(biāo)志位p，逼近偏差d>=0，節(jié)點(diǎn)Ni（1<=i<=m），參數(shù)對(duì)ui,vi（1<=i<=m），三角形nj,1，nj,2，nj,3。參數(shù)只有當(dāng)參數(shù)顯示標(biāo)志位p＝1時(shí)才顯示。三角剖分逼近曲面的偏差d定義如下所示：

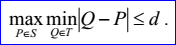
參數(shù)對(duì)ui，vi描述了曲面S上過(guò)節(jié)點(diǎn)Ni的參數(shù)：

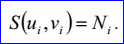
三角形nj,1， nj,2， nj,3用來(lái)取得三角形的三個(gè)頂點(diǎn)值Nnj,1，Nnj,2，Nnj,3，節(jié)點(diǎn)遍歷的順序就是Nnj,1，Nnj,2，Nnj,3。從三角剖分T的任意一側(cè)遍歷，所有三角形都有相同的方向：順時(shí)針或逆時(shí)針。

三角剖分中的三角形數(shù)據(jù)：

表示的三角剖分為：m＝4個(gè)節(jié)點(diǎn)，k＝2個(gè)三角形，參數(shù)顯示標(biāo)志位p＝1，逼近偏差d＝0，節(jié)點(diǎn)N1（0，0，0），N2（0，0，3），N3（0，2，3），N4（0，2，0），參數(shù)值（u1,v1）＝（0，0），（u2,v2）＝（3，0），（u3,v3）＝（3，－2），（u4,v4）＝（0，－2）。從點(diǎn)（1，0，0）（（－1，0，0）），三角形是順時(shí)針（逆時(shí)針）的。

四、程序示例 Code Example

通過(guò)創(chuàng)建多段線和三角網(wǎng)格數(shù)據(jù)并將其輸出，可以理解BRep文件中用來(lái)顯示的離散的數(shù)據(jù)結(jié)構(gòu)。程序示例如下所示：

輸出結(jié)果如下所示：

五、結(jié)論

通過(guò)對(duì)OpenCascade中BRep文件中的離散數(shù)據(jù)的學(xué)習(xí)，理解顯示用數(shù)據(jù)結(jié)構(gòu)及其實(shí)現(xiàn)。另外發(fā)現(xiàn)在類Poly和類BRepTools_ShapeSet中都有對(duì)多段線和三角網(wǎng)格進(jìn)行讀寫的函數(shù)，有重復(fù)代碼，可以合并簡(jiǎn)化。