|
|
Introduction

|
Hidden surface removal is among the biggest problems when writing a 3D engine.
I struggled with it since the very beginning of writing 3D engines and still have no satisfactory solution to it. The ideal visibility detection scheme would allow unlimited data, extremely dynamic worlds and would have zero overdraw. The first 3d engine which implements these three demands still has to be written.
The Z buffer for example allows dynamical worlds and even crossing faces, but it suffers from immense overdraw. The BSP-tree on the other hand, if well implemented, has no overdraw at all but needs that much pre-processing that dynamical worlds are a definite nono.
It wasn't until recently i first heard of the octree, and I must admit i was struck by it's simplicity. I never actually implemented this structure and therefore I will present no pseudo code at all. This explanation is merely an attempt to make it more clear to people who have never heard of it. Besides, if you really understand the structure, then implementation is a piece of cake. |
The Octree Structure

|
Our virtual world or level is actually nothing more then a soup of polygons. Some of you people might have thrown in a couple of curves and voxels but most of it will be polygons. Here it is:

Fig 1. Our little level.
In the picture I just built a simple level containing no more than 250 polys. Now imagine a cube surrounding the world like in the next image:
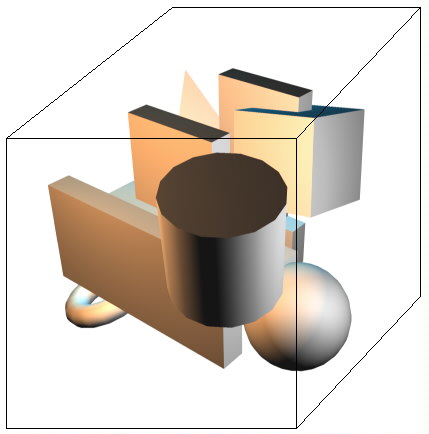
Fig. 2. Our little level surrounded by a cube.
Now it isn't hard to see that this cube can be divided into eight smaller cubes, hence the name octree. Take a look at this picture:

Fig 3. Our little level with the surrounding cube subdivided.
Call the larger cube the parent and the smaller cubes the children. On their turn subdivide each children into eight smaller cubes, and you will notice we are creating a tree where each node has eight children.
There is still one little problem left. When should we stop dividing cubes into smaller ones? There are two possible solutions. The first one is to stop when a cube has some size smaller then a fixed number. The second one is more common. You might have noticed that every child has less polygons then it's parent. The trick is to stop subdividing when the number of polygons in a cube is smaller then some fixed number. |
Creating The Octree

|
Trees are recursion, recursion is trees. It is as simple as that. If you have a correct definition of you cubeNode it is very easy to create an octree recursively. First of all you check all polygons against the boundarys of the cube. This is very simple cause these boundaries are all axis aligned. This means that the cube has six plane equations, which are:
1. X = Q.X
2. Y = Q.Y
3. Z = Q.Z
4. X = Q.X + cubeSize
5. Y = Q.Y + cubeSize
6. Z = Q.Z + cubeSize
Where Q is the position of one corner of the cube. This are very easy equations and the all parent polygons can very easily be checked against them.
It could occur that a polygon crosses a cube boundary. Again two possible solution are at hand. First of all we could clip the polygon against the cube, which is simple, because of the axis aligned boundarys. On the other hand we could put the polygon in all cubes it is in. This means that some cubes can contain the same polygons. In order to prevent us from drawing one poly more than one time we should have a flag on each polygon which will be set if the poly is drawn for the first time.
The implementation of an octree is very straight forward. I haven't done it myself yet, but I will soon. It is all matter of recursion. In order to construct a tree, the first thing you should think of is recursion. Whether we are talking about binary trees, quad trees or octrees, it doesnt matter, just build the darn thing recursively. So have a class definition of one cubeNode and put the creation of the tree in it's constructor. In this constructor you will call the constructor itself for smaller cubes.
|
The Purpose Of The Octree

|
An octree is actually nothing more then a data structure. It can be used for very different things. It is not only handy for visibility detection but also for collision detection, realtime shadows and many more things. The most important thing to understand about octrees is that if a parent is not important then it's children aren't either. Let's makes this a little bit more clear with an example.
We will do this in 2d, which therefore resembles a quadtree, but with some imagination it can very easily be extended to 3d. Here we test the cubes (squares) against the viewing frustrum. Take a look at the next picture:
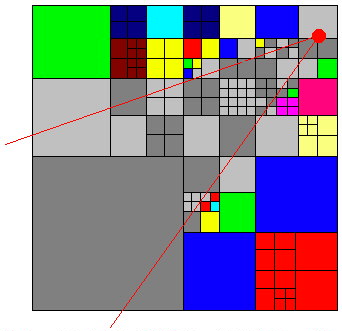
Fig 4. An octree from the top and a viewing frustrum.
In this picture a colored square that has one color was dumped without checking it?s children. As you can see some squares had to be checked all the way to the final node, but some large squares could be dumped at once. The colored squares are the ones that are outside the viewing frustrum and the greyscale ones are the one inside the viewing frustrum. As you can see this is actually a worst case scenario because the viewing frustrum crosses the middle of the surrounding square and therefore all the four children have to be checked.
You could also apply the octree to many other things. Collision detection for example. Just check in which cube your bounding sphere or box is and you will only have to check against those faces. There are many more examples. |
Conclusion

|
There is already a lot written about octrees. I tried to give my view on them in the hope somebody might read this. As you can see octrees are way easier to implement than BSP-trees (although some disagree) while offering a better structure. The main point about an octrees is that when a parent is discarded so are it's children. Actually that is all there is to it.
Code clean, play Goldeneye and go vegetarian.
Jaap Suter a.k.a ......... |
譯文:
1、引言(Introduction)
隱面移除是寫3D引擎時候最大的問題之一。
Hidden surface removal is among the biggest problems when writing a 3D engine.
在我寫3D引擎的開始階段就開始和它斗爭并且一直沒有滿意的解決方法。理想的可見檢測方案應當做到允許(使用)無限的數據、大動態的世界和零重畫。第一流的3D引擎一直在追求實現這3個要求。
I struggled with it since the very beginning of writing 3D engines and still have no satisfactory solution to it. The ideal visibility detection scheme would allow unlimited data, extremely dynamic worlds and would have zero overdraw. The first 3d engine which implements these three demands still has to be written.
Z buffer允許動態世界以及即使是交叉的面,但是得忍受大量的重畫。另一方面,BSP樹如果能夠被很好的實現,可以避免重畫,但是它需要大量的預處理計算而且不適合動態世界。
The Z buffer for example allows dynamical worlds and even crossing faces, but it suffers from immense overdraw. The BSP-tree on the other hand, if well implemented, has no overdraw at all but needs that much pre-processing that dynamical worlds are a definite nono.
直到最近我第一次聽說了八叉樹(Octree),我必須承認我被它的簡易性“狠狠地打了一下兒”。我從來沒有真正地去實現這個結構,因此我不會去實現一些代碼。這個解釋只是想讓從沒有聽說過八叉樹的人感到更清晰易懂。如果你真的了解了這個結構(Octree),實現它只是一個小意思。
It wasn't until recently i first heard of the octree, and I must admit i was struck by it's simplicity. I never actually implemented this structure and therefore I will present no pseudo code at all. This explanation is merely an attempt to make it more clear to people who have never heard of it. Besides, if you really understand the structure, then implementation is a piece of cake.
2、八叉樹的結構(The Octree Structure)
我們的實際‘世界’或者說是關卡只不過是一些多邊形。你們或許在其中加入了一些曲面(Curves)和Voxels(地形實現方法的一種),但是大多數也都是多邊形。
Our virtual world or level is actually nothing more then a soup of polygons. Some of you people might have thrown in a couple of curves and voxels but most of it will be polygons. Here it is:
 |
| 圖1 |
圖1:我們設計的小型關卡。
Fig 1. Our little level.
在這張圖片中我建立了一個不超過250個多邊形的‘關卡’。現在想象有一個包圍了這個世界的立方體,像下一張圖片那樣。
In the picture I just built a simple level containing no more than 250 polys. Now imagine a cube surrounding the world like in the next image:
 |
| 圖2 |
圖2:我們設計的關卡被一個立方體所包圍著。
Fig. 2. Our little level surrounded by a cube.
現在不難看出這個立方體可以被八等分為八個小些的立方體,所以才叫八叉樹。看看這張圖:
Now it isn't hard to see that this cube can be divided into eight smaller cubes, hence the name octree. Take a look at this picture:
 |
| 圖3 |
圖3:對圍繞著關卡的立方體進行細分。
Fig 3. Our little level with the surrounding cube subdivided.
大點兒的這個立方體被叫做‘父親’小些的立方體叫做‘孩子’。處理每個‘孩子’的時候,再為更小的八個立方體,你會發現我們在創建一個每個節點有八個子節點(孩子)的樹。
Call the larger cube the parent and the smaller cubes the children. On their turn subdivide each children into eight smaller cubes, and you will notice we are creating a tree where each node has eight children.
還有一個小問題。什么時候我們該結束細分的過程呢?有兩個可行的解決方法。第一個是當一個立方體的尺寸已經比一個預定的固定值小的時候。第二個更普通。你可以注意到每個‘孩子’都比他的‘父親’有更少的多邊形。這就是說:當一個立方體包含的多邊形數量比一個預定的固定值少的時候停止細分。
There is still one little problem left. When should we stop dividing cubes into smaller ones? There are two possible solutions. The first one is to stop when a cube has some size smaller then a fixed number. The second one is more common. You might have noticed that every child has less polygons then it's parent. The trick is to stop subdividing when the number of polygons in a cube is smaller then some fixed number.
3、創建八叉樹(Creating The Octree)
樹是遞歸的,遞歸的是樹。就那么簡單。如果你正確的定義了你的立方體節點,那么遞歸地創建一個八叉樹是很容易的。首先,檢查所有的多邊形(多邊形上位置最外面的點作為)立方體的邊界。這很簡單因為所有邊界都是和坐標軸對其的。這意味著立方體有六個平面方程,分別是:
Trees are recursion, recursion is trees. It is as simple as that. If you have a correct definition of you cubeNode it is very easy to create an octree recursively. First of all you check all polygons against the boundarys of the cube. This is very simple cause these boundaries are all axis aligned. This means that the cube has six plane equations, which are:
- 1. X = Q.X
- 2. Y = Q.Y
- 3. Z = Q.Z
- 4. X = Q.X + cubeSize
- 5. Y = Q.Y + cubeSize
- 6. Z = Q.Z + cubeSize
在這里Q是立方體一個頂角的位置。這是個很簡單的方程,而且所有的父親多邊形可以容易地用這些方程來檢測。
WhereQ is the position of one corner of the cube. This are very easy equations and the all parent polygons can very easily be checked against them.
一個多邊形穿過了一個立方體邊界這樣的事情是會發生的。再一次,有兩個解決方案可用。首先我們可以沿著立方體剪切這個多邊形,這也是很簡單的,因為(立方體的)邊界是與坐標軸對齊的。還有,我們可以把一個多邊形放在所有它所在的立方體里面。這就意味著一些立方體可能包含著同一個多邊形。為了防止重畫一個多邊形,我們應當在每一個多邊形上做一個標記,當多邊形第一次被畫的時候,設置這個標記(當然畫之前也要檢查這個標記啦,不過肯定影響效率。
It could occur that a polygon crosses a cube boundary. Again two possible solution are at hand. First of all we could clip the polygon against the cube, which is simple, because of the axis aligned boundarys. On the other hand we could put the polygon in all cubes it is in. This means that some cubes can contain the same polygons. In order to prevent us from drawing one poly more than one time we should have a flag on each polygon which will be set if the poly is drawn for the first time.
實現一個八叉樹是很簡單明了的事情,我還沒有自己做過,但是我不久會做的。只不過是遞歸而已。為了構造一個樹,第一件你該想的事情就是遞歸。不管我們討論的是二叉、四叉還是八叉樹,都沒有區別,都是遞歸的方法。所以定義一個立方體節點的類,在構造函數里面寫上創建樹的代碼。在這個構造函數里面,你會調用到更小立方體的構造函數。
The implementation of an octree is very straight forward. I haven't done it myself yet, but I will soon. It is all matter of recursion. In order to construct a tree, the first thing you should think of is recursion. Whether we are talking about binary trees, quad trees or octrees, it doesnt matter, just build the darn thing recursively. So have a class definition of one cubeNode and put the creation of the tree in it's constructor. In this constructor you will call the constructor itself for smaller cubes.
4、八叉樹的用途(The Purpose Of The Octree)
一個八叉樹實際上就是一個數據結構。它可以用做不同的事情。不僅僅對于‘可見檢測’來說很方便,還有實時陰影以及其它方面。理解八叉樹過程中最重要的事情是:如果一個‘父親’節點是‘沒用’的,那么他的‘孩子’節點也同樣。讓我們舉個例子讓它更清楚。
An octree is actually nothing more then a data structure. It can be used for very different things. It is not only handy for visibility detection but also for collision detection, realtime shadows and many more things. The most important thing to understand about octrees is that if a parent is not important then it's children aren't either. Let's makes this a little bit more clear with an example.
我們用2D來表示它,這樣就很像一個四叉樹,但是想象一下它也可以很容易的擴展到3D上。在這里我們沿著視錐(viewing frustrum)檢測立方體(正方形)。
We will do this in 2d, which therefore resembles a quadtree, but with some imagination it can very easily be extended to 3d. Here we test the cubes (squares) against the viewing frustrum. Take a look at the next picture:
 |
| 圖4 |
圖4:頂部視錐內的八叉樹。
Fig 4. An octree from the top and a viewing frustrum.
在這個圖片中,彩色的正方形是沒有(沒必要)檢測它的‘孩子’的。就像你看到的那樣一些正方形(灰色的一些)被檢測直到最終節點,但是一些大的正方形只被涂了一種顏色。那些彩色的正方形就是超出了視錐范圍的,灰色的是在視錐范圍內的。就像你看到的那樣,這確實是最糟糕的一種情況,因為視錐穿過了包圍正方形的中央,所以所有的四個‘孩子’都得被檢測。
In this picture a colored square that has one color was dumped without checking it抯 children. As you can see some squares had to be checked all the way to the final node, but some large squares could be dumped at once. The colored squares are the ones that are outside the viewing frustrum and the greyscale ones are the one inside the viewing frustrum. As you can see this is actually a worst case scenario because the viewing frustrum crosses the middle of the surrounding square and therefore all the four children have to be checked.
你可以應用八叉樹到很多別的地方。例如碰撞檢測。只檢查你的碰撞球或者碰撞盒子所在的立方體,而且只需要檢測那些面。還有更多的例子。
You could also apply the octree to many other things. Collision detection for example. Just check in which cube your bounding sphere or box is and you will only have to check against those faces. There are many more examples.
5、結論(Conclusion)
關于八叉樹已經寫了很多了。我設法表述自己對它的看法,并且希望有人會讀到它。就像你看到的那樣,當提供好的結構的時候,八叉樹比BSP樹更容易實現(有人持異議)。主要的一點是:當一個‘父親’節點被丟棄的時候,他的‘孩子’節點也同樣被丟棄。實際上這就是全部。
There is already a lot written about octrees. I tried to give my view on them in the hope somebody might read this. As you can see octrees are way easier to implement than BSP-trees (although some disagree) while offering a better structure. The main point about an octrees is that when a parent is discarded so are it's children. Actually that is all there is to it.
Code clean, play Goldeneye and go vegetarian. Jaap Suter a.k.a .........

|