新建網(wǎng)頁 1
重心坐標空間
雖然我們經(jīng)常在3D中使用三角形,但三角形的表面是一個平面,它天生是一個2D物體。在3D中任意朝向的三角形表面上移動是一件令人煩惱的事,最好是有一個坐標空間與三角形表面相關聯(lián)且獨立于三角形所在的3D坐標空間,重心坐標空間正是這樣的坐標空間。
三角形所在平面的任意點都能表示為頂點的加權(quán)平均值,這個權(quán)就稱作重心坐標,從重心坐標(b1,b2,b3)到標準3D坐標的轉(zhuǎn)換為:
(b1,b2,b3) <==> b1v1 + b2v2 + b3v3
公式12.21 從重心坐標中計算3D點坐標
重心坐標的和總是1:
b1 + b2 + b3 = 1
b1、b2和b3的值是每個頂點對該點的"貢獻"或"權(quán)"。圖12.19展示了一些點和它們的重心坐標。
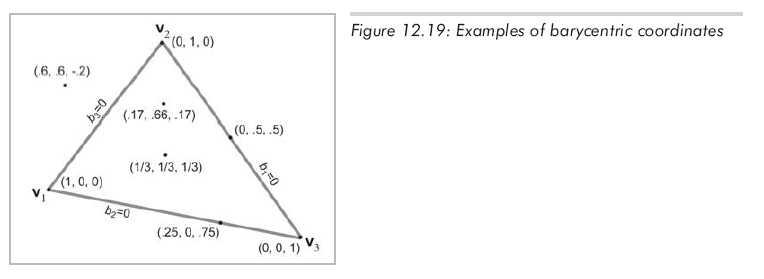
這里應注意以下幾點:
(1)三角形三個頂點的重心坐標都是單位向量:
(1, 0, 0) <==> v1
(0, 1, 0) <==> v2
(0, 0, 1) <==> v3
(2)在某頂點的相對邊上的所有點的對應重心坐標分量為0。例如,對于所有與v1相對邊上的點,b1=0。
(3)不只是三角形內(nèi)的點,該平面上的所有點都能用重心坐標描述。三角形內(nèi)點的重心坐標在范圍0到1之間變化,三角形外的點至少有一個坐標為負。重心坐標用和原三角形大小相同的塊嵌滿整個平面,如圖12.20所示:

重心坐標空間的本質(zhì)不同于笛卡爾坐標空間。這是因為重心坐標空間是2D的,但卻使用了三個坐標。又因為坐標的和等于1,所以重心坐標空間僅有兩個自由度,有一個分量是冗余的。從另一方面說,重心坐標空間中僅用兩個數(shù)就能完全的描述一個點,用這兩個數(shù)就可以計算出第三個。
要將一個點從重心坐標空間轉(zhuǎn)換到普通的3D坐標空間,只需要應用公式12.21來計算頂點加權(quán)平均值就可以了。而計算2D或3D中任意一點的重心坐標就稍微困難一些。讓我們看看怎樣在2D中做到這一點。見圖12.21,它標出了三個頂點v1、v2、v3和p。我們還標出了三個"子三角形"T1、T2、T3,它們和同樣下標的頂點相對。
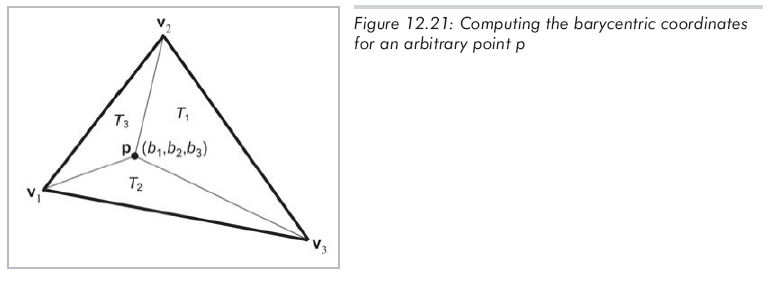
現(xiàn)在,我們知道的是三個頂點和點p的笛卡爾坐標,而任務就是要計算重心坐標b1,b2和b3。根據(jù)這些已知條件可以列出三個等式和三個未知數(shù)(x,y為頂點)

仔細觀察公式12.22,發(fā)現(xiàn)每個表達式中的分母相同,并且都等于三角形面積的兩倍(根據(jù)公式12.20)。還有,對每個重心坐標bi,其分子等于"子三角形"Ti面積的兩倍。換據(jù)說說:
b1 = A(T1) / A(T)
b2 = A(T2) / A(T)
b3 = A(T3) / A(T)
公式12.23 把重心坐標解釋為面積比
注意,即使p在三角形外,這個解釋也是成立的,這是因為如果頂點以逆時針方向列出,計算面積的公式將得到一個負值。如果三角形的三個頂點共線,分母上的"子三角形"的面積為0,重心坐標也就沒有定義。
計算3D中任意點的重心坐標比在2D中復雜,不能再像以前那樣解一個方程組了,因為有三個未知數(shù)和四個方程。另一個導致復雜性的地方是p可能不在三角形所在的平面中,這時重心坐標沒有意義,但現(xiàn)在我們假設p在三角形所在的平面上。
一種技巧是通過拋棄x、y、z中的一個分量,將3D問題轉(zhuǎn)化到2D中,這和將三角形投影到三個基本平面中某一個上的原理相同。理論上,這是能解決問題的,因為投影面積和原面積成比例。
那么應該拋棄哪個坐標呢?不能總是拋棄某一個,因為如果三角形垂直于某個平面,投影點將共線。如果三角形接近垂直于投影平面,會遇到浮點數(shù)精度問題。一種解決方法是挑選投影平面,使得投影面積最大。這可以通過檢查平面的法向量做到,我們要拋棄的就是絕對值最大的坐標。例如,法向量為[-1, 0, 0],我們將拋棄頂點p的x分量,把三角形投影到yz平面。下面的代碼展示了怎樣計算3D中任意點的重心坐標:
Listing 12.3: Computing barycentric coordinates in 3D
bool computeBarycentricCoords3d(
const Vector3 v[3], // vertices of the triangle
const Vector3 &p, // point that we wish to compute coords for
float b[3] // barycentric coords returned here
)
{
// First, compute two clockwise edge vectors
Vector3 d1 = v[1] – v[0];
Vector3 d2 = v[2] – v[1];
// Compute surface normal using cross product. In many cases
// this step could be skipped, since we would have the surface
// normal precomputed. We do not need to normalize it, although
// if a precomputed normal was normalized, it would be OK.
Vector3 n = crossProduct(d1, d2);
// Locate dominant axis of normal, and select plane of projection
float u1, u2, u3, u4;
float v1, v2, v3, v4;
if ((fabs(n.x) >= fabs(n.y)) && (fabs(n.x) >= fabs(n.z)))
{
// Discard x, project onto yz plane
u1 = v[0].y – v[2].y;
u2 = v[1].y – v[2].y;
u3 = p.y – v[0].y;
u4 = p.y – v[2].y;
v1 = v[0].z – v[2].z;
v2 = v[1].z – v[2].z;
v3 = p.z – v[0].z;
v4 = p.z – v[2].z;
}
else if (fabs(n.y) >= fabs(n.z))
{
// Discard y, project onto xz plane
u1 = v[0].z – v[2].z;
u2 = v[1].z – v[2].z;
u3 = p.z – v[0].z;
u4 = p.z – v[2].z;
v1 = v[0].x – v[2].x;
v2 = v[1].x – v[2].x;
v3 = p.x – v[0].x;
v4 = p.x – v[2].x;
}
else
{
u1 = v[0].x – v[2].x;
u2 = v[1].x – v[2].x;
u3 = p.x – v[0].x;
u4 = p.x – v[2].x;
v1 = v[0].y – v[2].y;
v2 = v[1].y – v[2].y;
v3 = p.y – v[0].y;
v4 = p.y – v[2].y;
}
// Compute denominator, check for invalid
float denom = v1 * u2 – v2 * u1;
if (denom == 0.0f)
{
// Bogus triangle - probably triangle has zero area
return false;
}
// Compute barycentric coordinates
float oneOverDenom = 1.0f / denom;
b[0] = (v4*u2 – v2*u4) * oneOverDenom;
b[1] = (v1*u3 – v3*u1) * oneOverDenom;
b[2] = 1.0f – b[0] – b[1];
// OK
return true;
}
另一種計算3D重心坐標的方法基于用向量叉乘計算3D
三角形面積的方法。給出三角形的兩個邊向量e1和e2,三角形面積為||
e1x
e2|| / 2
。一旦有了整個三角形的面積和三個"
子三角形"的面積,就能計算重心坐標了。
還有一個小小的問題:叉乘的大小對頂點的順序不敏感。根據(jù)定義,叉乘大小總是正的。這種方法不適用于三角形外的點,因為它們至少有一個負的重心坐標。
看看能否找到解決問題的思路。當頂點以"不正確"的順序列出時,向量叉乘的大小可能會是負值,我們需要一種正確計算的方法。幸運的是,有一種非常簡單的方法能做到這一點:點乘。
設c為三角形兩個邊向量的叉乘,c的大小等于三角形面積的兩倍。設有一個單位法向量n,n和c是平行的,因為它們都垂直于三角形所在的平面。當然,它們的方向可能是相反的。兩向量的點乘等于它們大小的積再乘以它們夾角的cos值。因為n是單位向量,不管n和c方向相同還是相反,都有:
c . n = ||c|| ||n|| cosθ = ||c|| (1) (±1) = ±||c||
將這個面積除以2,就得到了3D中三角形的"有符號"面積。有了這個技巧,就能利用前一節(jié)的結(jié)論:bi就是"子三角形"Ti的面積占整個三角形面積的比。如圖12.22所示,標出了所有用到的向量。
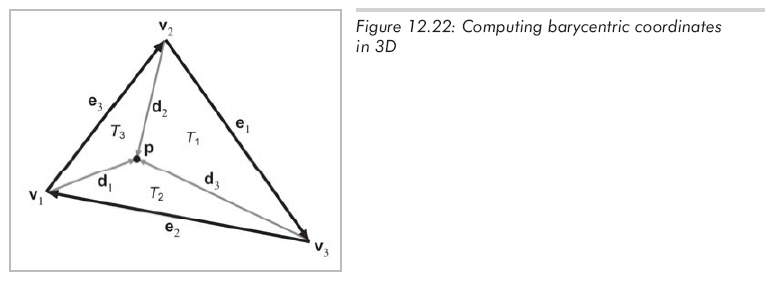
正如你所看到的,每個頂點都有一個向量di,它從vi指向p,列出這些向量滿足的方程:

注意到所有的分子和分母中都有n,因此,實際上并不必單位化n。此時,分母為n . n。
這種計算重心坐標的方法比向2D投影的方法用到了更多的標量數(shù)學運算。但是它沒有分支,并為向量處理器提供了更多的優(yōu)化機會。因此它在有向量處理器的超標量體系結(jié)構(gòu)中會更快一些。
特殊點
重心是三角形的最佳平衡點,它是三角形三條中線的交點(中線指從頂點到對邊中點的連線)。圖12.23展示了一個三角形的重心。
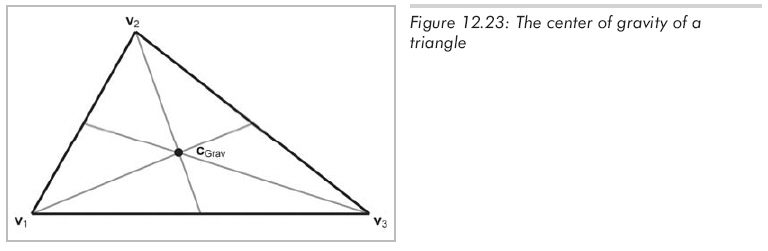
重心是三個頂點的幾何均值:
cgrav = (v1+ v2 + v3) / 3
重心坐標為:
(1/3, 1/3, 1/3)
重心也被稱作質(zhì)心。
內(nèi)心是指到三角形各邊距離相等的點。之所以稱作內(nèi)心是因為它是三角形內(nèi)切圓的圓心,內(nèi)心是角平分線的交點,如圖12.24所示:

內(nèi)心的計算:
cin = (L1v1 + L2v2 + L3v3) / p
p = L1 + L2 + L3是三角形的周長,因此,內(nèi)心的重心坐標為:
(L1/p, L2/p,L3/p)
內(nèi)切圓的半徑可由三角形面積除以周長求得:
rin = A/p
內(nèi)切圓解決了尋找與三條直線相切的圓的問題。
外心是三角形中到各頂點距離相等的點,它是三角形外接圓的圓心。外心是各邊垂直平分線的交點。圖12.25展示了一個三角形的外心。

為了計算外心,先定義以下臨時變量:

外心和外接圓半徑解決了尋找過三個點的圓的問題。