一般來說，投影意味著降維操作，有一種投影方法是在某個方向上用0作為縮放因子。這種情況下，所有點都被拉平至垂直的軸（2D）或平面（3D）上。這種類型的投影稱作正交投影（或者平行投影），因為從原來的點到投影點的直線相互平行。

向坐標軸或平面投影

最簡單的投影方式是向坐標軸（2D）或平面（3D）投影，如圖8.15所示：

向坐標軸或平面投影在實際變換中不常發生，大多數情況是向低維的變換賦值，且要拋棄維數時。例如，將3D點賦值給2D點，拋棄z分量，只復制x和y。

通過使垂直方向上的縮放因子為零，就能向坐標軸或平面投影。考慮到完整性，下面列出這些變換矩陣，見公式8.10 - 8.14。

向任意直線或平面投影

也能向任意直線或平面投影，像往常一樣，由于不考慮平移，這些直線或平面必須通過原點。投影由垂直于直線或平面的單位向量n定義。

通過使該方向的縮放因子為0能夠導出向任意方向投影的矩陣，2D中的情況如公式8.15所示：

記住這里n垂直于投影直線，而不是平行。3D中，向垂直于n的平面投影的矩陣如公式8.16所示：

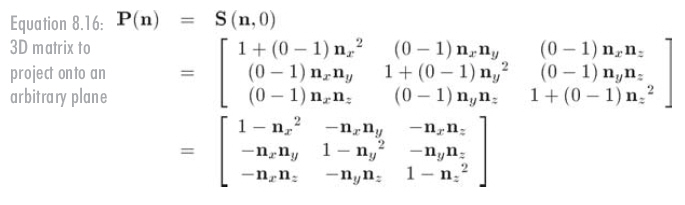
鏡像

鏡像（也叫做反射）是一種變換，其作用是將物體沿直線（2D中）或平面（3D中）“翻折”，圖8.16展示了鏡像的效果。

使縮放因子為-1能夠很容易地實現鏡像變換，設n為2D單位向量，公式8.17所示的矩陣將沿通過原點且垂直于n的反射軸來進行鏡像變換。

3D中，用反射平面代替直線。公式8.18中的矩陣將沿通過原點且垂直于n的平面來進行鏡像變換：

注意一個物體只能“鏡像”一次，如果再次鏡像（當沿不同的軸或平面的時候），物體將翻回“正面”（用一張紙來想象），這和在原位置旋轉物體的效果一樣。

切變

切變是一種坐標系“扭曲”變換，非均勻地拉伸它。切變的時候角度會發生變化，但令人驚奇的是面積和體積卻保持不變。基本思想是將某一坐標的乘積加到另一個上。例如，2D中將y乘以某個因子然后加到x上，得到 x' = x + sy，如圖8.17所示：

實現這個切變變換的矩陣為：