Posted on 2019-11-21 13:17
eryar 閱讀(5015)
評論(0) 編輯 收藏 引用 所屬分類:
2.OpenCASCADE
最小二乘法擬合三維直線
eryar@163.com
在《高等數學》的書中給出了最小二乘法擬合直線的具體實例，但是那個例子是擬合二維直線的f(t)=at+b，那么三維直線怎么使用最小二乘法來擬合呢？我們先來看看《高等數學》書中的例子，由于任何實數的平方都是正數或零，因此我們可以考慮選取常數a, b，使
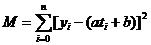
M最小來保證每個偏差的絕對值都很小，這種根據偏差的平方和為最小的條件來選擇常數a, b的方法叫做最小二乘法（Least Square）。因為M是平方和，所以M的最小值在導數等于零的時候取得，即：
根據這個條件計算得到的最小值就是最小二乘解。因為擬合函數是二維直線方程f(t)=at+b是線性的，所以二維直線的擬合是線性最小二乘問題。對于三維直線，如果選擇其代數方程，是兩個平面的交線來表達的：
可以看出待確定的參數有8個，不是一個好辦法。可以采用直線的參數表達，根據直線的對稱式方程導出直線的參數方程：
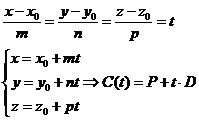
我們要做的是根據N個采樣點Pi確定參數方程的P和D，使所有采樣點到直線的距離的平方和最小。對于三維點到三維直線的距離我們可以使用矢量方法來計算，可以參考《點向直線投影》，
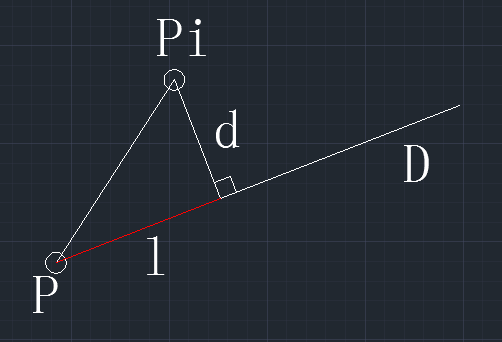
向量V為P到采樣點Pi的向量，向量D為直線的方向向量，是單位向量。V和D點乘得到V向D的投影長度，即圖中紅色標示部分的長度l。則采樣點到直線的距離的平方是向量V的模的平方減去投影長度l的平方。從而得到采樣點到直線的距離平方和方程：
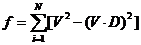
參考“最小二乘法三維(k維)直線擬合http://www.whudj.cn/?p=72”可知，最小二乘法擬合的直線通過所有采樣點的中心點。即可以確定直線參數方程中的P。這樣最小二乘方程就是只有方向矢量的一個多元函數。使用類math_MultipleVarFunctionWithGradient來建立上述最小二乘方程：
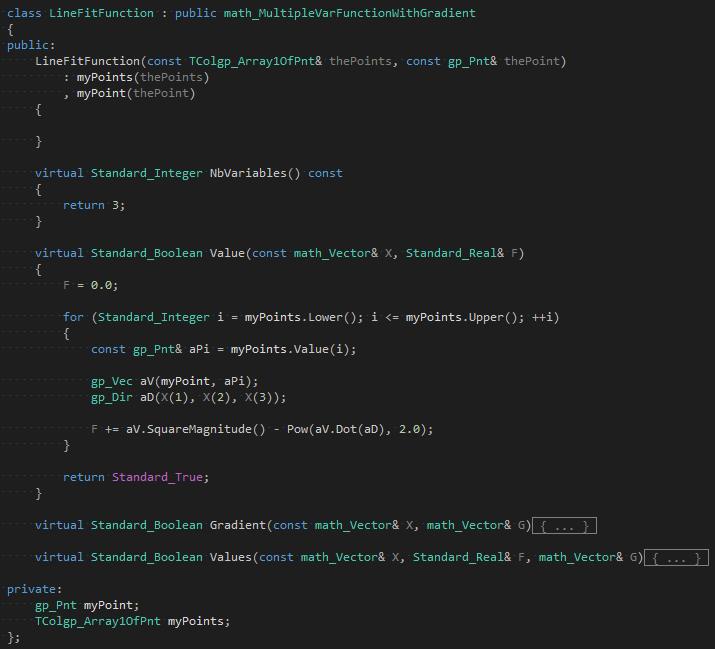
其中成員變量myPoint是直線的中心點，myPoints是所有的采樣點。最小二乘方程為確定直線參數方程中的方向矢量（dx, dy, dz）的三個變量方程。使用math_BFGS之類的非線性極值計算類來對這個最小二乘方程進行求解。下面給出幾個測試用例：
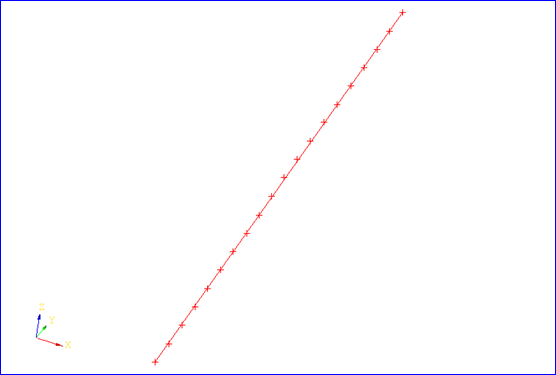
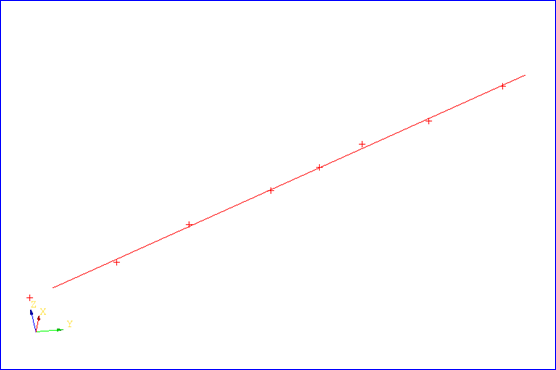
綜上所述，擬合三維直線的最小二乘方程中點到直線的距離為點到直線的垂直距離，而書中二維直線擬合只是兩個y值之間的差值：
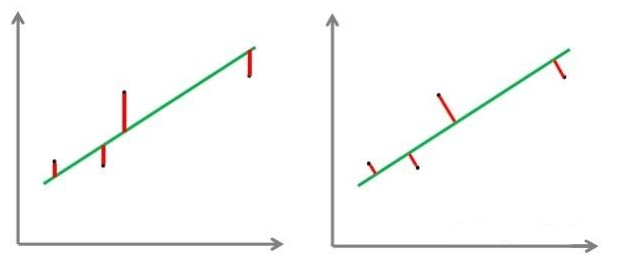
圖 點到直線的距離 （來自：https://zhuanlan.zhihu.com/p/36429715）
上述擬合過程也可看出三維直線的擬合是一個非線性的優化問題，處理這類問題的一般步驟就是先建立目標方程，再使用相關優化求解類來對方程進行求解。
為了方便大家在移動端也能看到我的博文和討論交流，現已注冊微信公眾號，歡迎大家掃描下方二維碼關注。
