最小二乘法擬合直線
在科學實驗和生產實踐中,經常需要從一組實驗數據出發尋求函數y=f(x)的一個近似表達式,也稱為經驗公式。從幾何上看,就是希望根據給定的m個點,求曲線y=f(x)的一條近似曲線。因此這是個曲線擬合問題。
當我們要求近似曲線嚴格通過給定的每個點時,這是插值算法。對于本文所述的直線擬合來說,如果用插值算法,則只需要兩個點就夠了。實際直線擬合數據可能滿足不了這個條件,為了便于計算,分析與應用,我們較多地根據“使測量點到直線距離的平方和最小”的原則來擬合。按最小二乘原則選擇擬合曲線的方法,稱為最小二乘法(Method of Least Squares)。
利用最小二乘法擬合曲線的一般步驟是:
-
將實驗數據顯示出來,分析曲線的形式;
-
確定擬合曲線的形式。對于本文來說,曲線形式是直線,y=a+bx;
-
建立法方程組并對其進行求解;
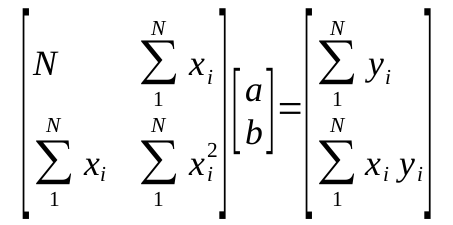
因為OpenCASCADE中數據結構及算法豐富,所以用OpenCASCADE可以快速實現直線的最小二乘法擬合算法。下面給出具體實現代碼:
#include <iostream> #include <gp_Lin2d.hxx> #include <gp_Pnt2d.hxx> #include <TColgp_Array1OfPnt2d.hxx> #include <math_Vector.hxx> #include <math_SVD.hxx> #include <math_Gauss.hxx> #include <math_GaussLeastSquare.hxx> #include <OSD_Chronometer.hxx> void fitLine(const TColgp_Array1OfPnt2d& thePoints, const std::string& theFileName, gp_Lin2d& theLine) { math_Vector aB(1, 2, 0.0); math_Vector aX(1, 2, 0.0); math_Matrix aM(1, 2, 1, 2); Standard_Real aSxi = 0.0; Standard_Real aSyi = 0.0; Standard_Real aSxx = 0.0; Standard_Real aSxy = 0.0; std::ofstream aDrawFile(theFileName); for (Standard_Integer i = thePoints.Lower(); i <= thePoints.Upper(); ++i) { const gp_Pnt2d& aPoint = thePoints.Value(i); aSxi += aPoint.X(); aSyi += aPoint.Y(); aSxx += aPoint.X() * aPoint.X(); aSxy += aPoint.X() * aPoint.Y(); aDrawFile << "vpoint p" << i << " " << aPoint.X() << " " << aPoint.Y() << " 0" << std::endl; } aM(1, 1) = thePoints.Size(); aM(1, 2) = aSxi; aM(2, 1) = aSxi; aM(2, 2) = aSxx; aB(1) = aSyi; aB(2) = aSxy; OSD_Chronometer aChronometer; aChronometer.Start(); math_Gauss aSolver(aM); //math_GaussLeastSquare aSolver(aM); //math_SVD aSolver(aM); aSolver.Solve(aB, aX); if (aSolver.IsDone()) { Standard_Real aA = aX(1); Standard_Real aB = aX(2); gp_Pnt2d aP1(0.0, aA); gp_Pnt2d aP2(-aA/aB, 0.0); theLine.SetLocation(aP1); theLine.SetDirection(gp_Vec2d(aP1, aP2).XY()); aDrawFile << "vaxis l " << aP1.X() << " " << aP1.Y() << " 0 " << aP2.X() << " " << aP2.Y() << " 0 " << std::endl; std::cout << "===================" << std::endl; aX.Dump(std::cout); } aChronometer.Stop(); aChronometer.Show(); } int main() { gp_Lin2d aLine; // Test data 1 TColgp_Array1OfPnt2d aPoints1(1, 6); aPoints1.SetValue(1, gp_Pnt2d(36.9, 181.0)); aPoints1.SetValue(2, gp_Pnt2d(46.7, 197.0)); aPoints1.SetValue(3, gp_Pnt2d(63.7, 235.0)); aPoints1.SetValue(4, gp_Pnt2d(77.8, 270.0)); aPoints1.SetValue(5, gp_Pnt2d(84.0, 283.0)); aPoints1.SetValue(6, gp_Pnt2d(87.5, 292.0)); fitLine(aPoints1, "fit1.tcl", aLine); // Test data 2 TColgp_Array1OfPnt2d aPoints2(0, 7); aPoints2.SetValue(0, gp_Pnt2d(0.0, 27.0)); aPoints2.SetValue(1, gp_Pnt2d(1.0, 26.8)); aPoints2.SetValue(2, gp_Pnt2d(2.0, 26.5)); aPoints2.SetValue(3, gp_Pnt2d(3.0, 26.3)); aPoints2.SetValue(4, gp_Pnt2d(4.0, 26.1)); aPoints2.SetValue(5, gp_Pnt2d(5.0, 25.7)); aPoints2.SetValue(6, gp_Pnt2d(6.0, 25.3)); aPoints2.SetValue(7, gp_Pnt2d(7.0, 24.8)); fitLine(aPoints2, "fit2.tcl", aLine); return 0; }
在函數fitLine()中,根據擬合點建立法方程組,并使用math_Gauss來對法方程組進行求解。其實也可以使用math_GaussLeastSquare或者math_SVD等求解法方程組。在主函數main()中測試了兩組數據。測試數據1來自易大義等《計算方法》,測試數據2來自《高等數學》。程序運行結果如下圖所示:
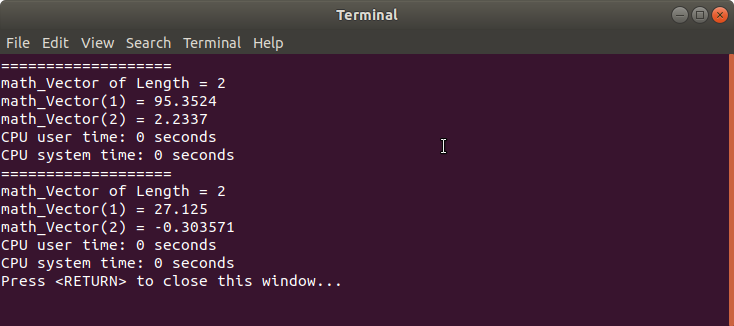
與書中計算結果吻合。
由于需要將計算結果顯示出來,所以在fitLine()函數中增加了輸出Draw腳本文件的代碼,實際運用時可將這部分代碼去掉。將程序生成的腳本文件加載到Draw中,即可得到下面兩個圖:
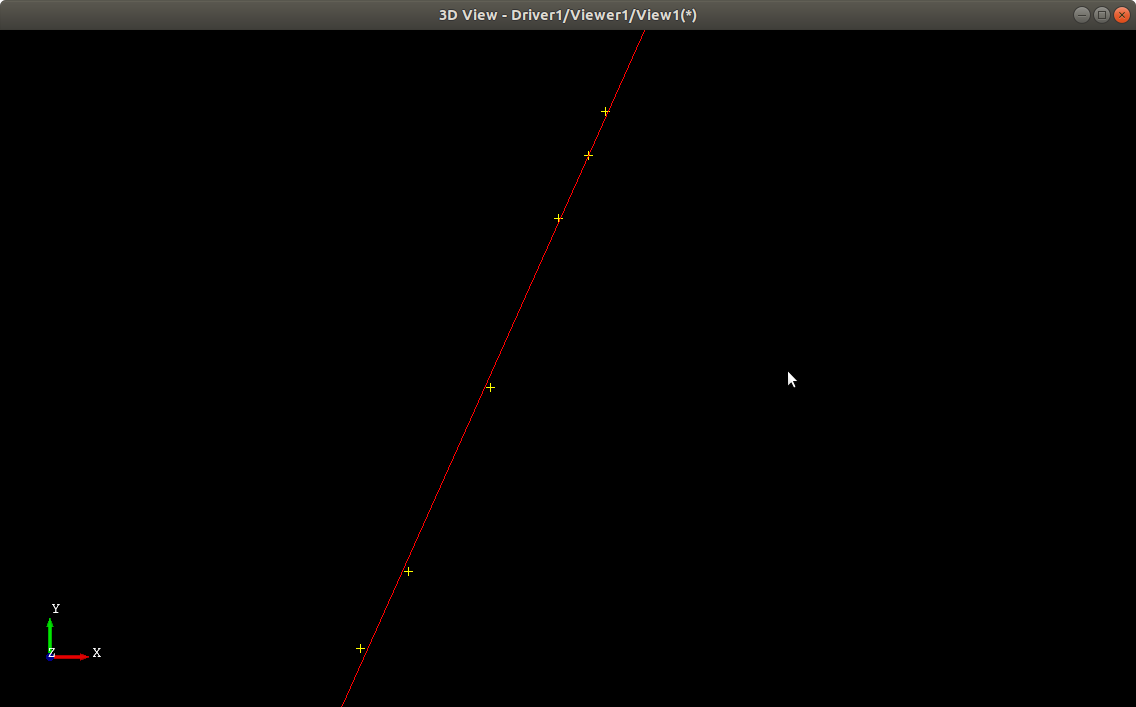
測試數據1擬合直線

測試數據2擬合直線
綜上所述,對于二維直線的最小二乘法擬合算法的關鍵是對建立的法方程組進行求解。OpenCASCADE的math包中提供了一些解方程組的類可以直接使用。對于沒有使用OpenCASCADE的開發環境的情況,也可以使用其他矩陣庫,如Eigen等用得很廣泛。Eigen官方網站:http://eigen.tuxfamily.org/index.php?title=Main_Page
將計算結果導出Draw腳本可視化,可以方便直觀地查看擬合結果。如果熟悉其他腳本庫如Python的matplotlib,也可以類似處理來將結果可視化。





