Mesh BRep Shapes
eryar@163.com
Abstract. 當(dāng)對(duì)OpenCASCADE的BRep表示法的數(shù)據(jù)結(jié)構(gòu)有了一定的理解后，建議可以自己實(shí)現(xiàn)一個(gè)顯示數(shù)據(jù)生成的功能，即網(wǎng)格剖分功能。
Key Words. BRep, Mesh, Triangulation
1. Introduction
在OpenCASCADE中網(wǎng)格剖分功能是很重要的一個(gè)模塊，他可用于生成模型的可視化數(shù)據(jù)，還可用于HLR消隱，對(duì)于離散求交算法也是基于網(wǎng)格數(shù)據(jù)。OpenCASCADE開源版本中的模塊TKMesh可以用來(lái)生成網(wǎng)格的顯示數(shù)據(jù)，主要的類為BRepMesh_IncrementalMesh。
在使用BRepMesh_IncrementalMesh的過(guò)程中發(fā)現(xiàn)其剖分精度高，且精度不便于控制。如對(duì)一個(gè)球進(jìn)行網(wǎng)格剖分，想得到一個(gè)粗糙的效果，即一個(gè)多邊形，使用BRepMesh_IncrementalMesh是不容易得到的。
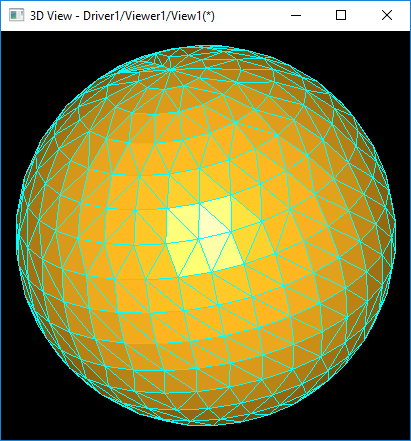
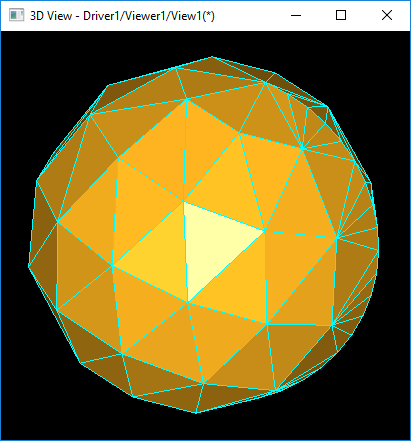
如上圖所示為同一個(gè)球的不同的剖分精度得到的模型。為了能精確控制網(wǎng)格剖分精度，以便后期使用LOD等優(yōu)化算法，自己實(shí)現(xiàn)一個(gè)網(wǎng)格剖分功能。
網(wǎng)格剖分的主要思路就是遍歷每個(gè)TopoDS_Face的TopoDS_Wire，根據(jù)Wire找到邊界或面上的孔洞。將Wire對(duì)應(yīng)到二維參數(shù)空間，并對(duì)二維參數(shù)空間中的邊界先進(jìn)行一次三角網(wǎng)格剖分。對(duì)于平面來(lái)說(shuō)，只需要這一步就可以滿足可視化的要求。對(duì)于其他曲面來(lái)說(shuō)，就需要在二維參數(shù)空間中額外插入一些點(diǎn)，以使最終生成的網(wǎng)格滿足剖分精度要求。最后將二維參數(shù)空間的三角剖分映射到三維空間。
2. Mesh Boundary Region
因?yàn)槭褂?/span>BRepBuilderAPI_MakeFace可以通過(guò)Add(TopoDS_Wire)來(lái)添加面上的開孔，所以一個(gè)TopoDS_Face會(huì)有大于1個(gè)的TopoDS_Wire。找出外邊界和內(nèi)孔Wire后可進(jìn)行一次三角剖分，如下圖所示：
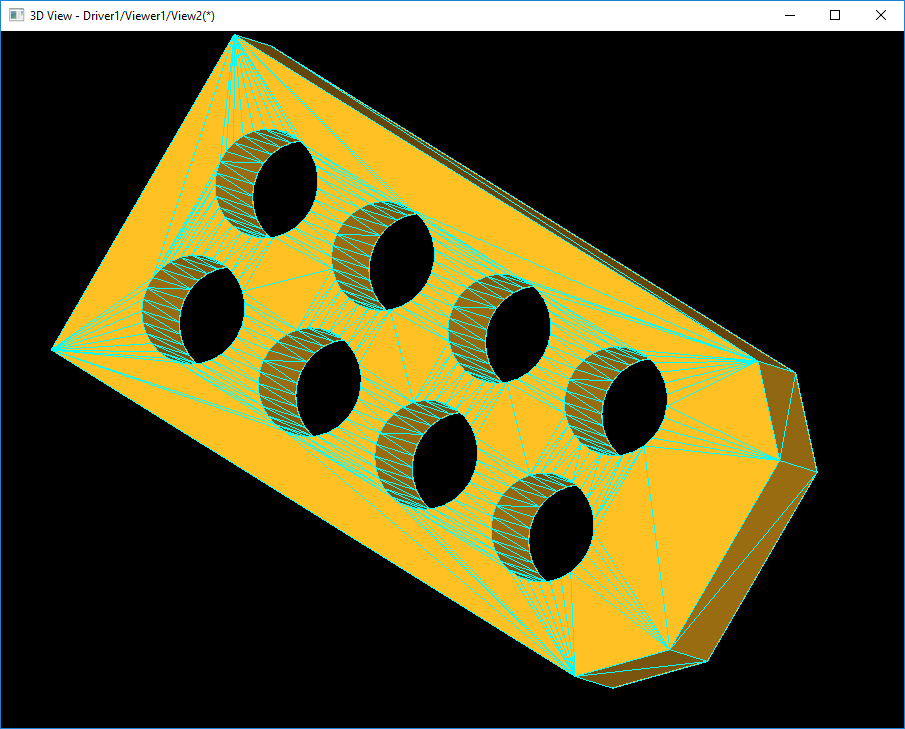
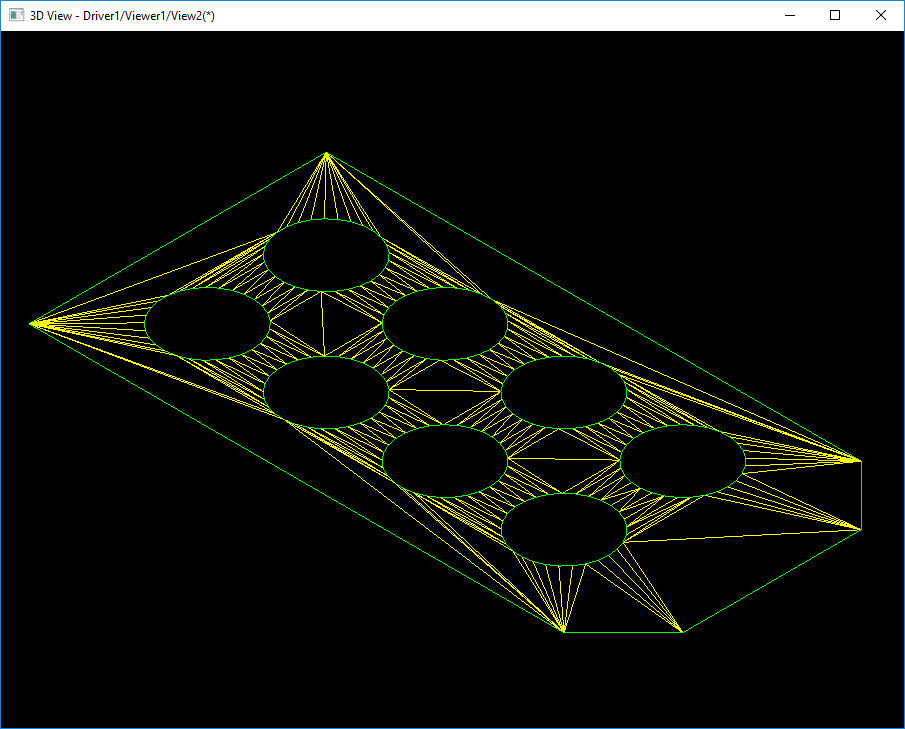
如上圖所示，對(duì)于平面而言，直接對(duì)邊界及內(nèi)孔進(jìn)行一次三角剖分即可以得到滿意的網(wǎng)格數(shù)據(jù)。對(duì)于曲面而言，這顯然是不滿足精度要求的。
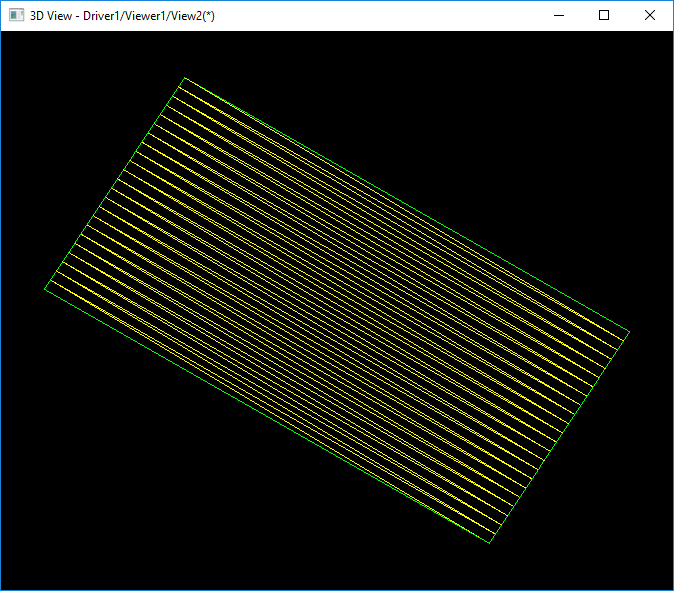
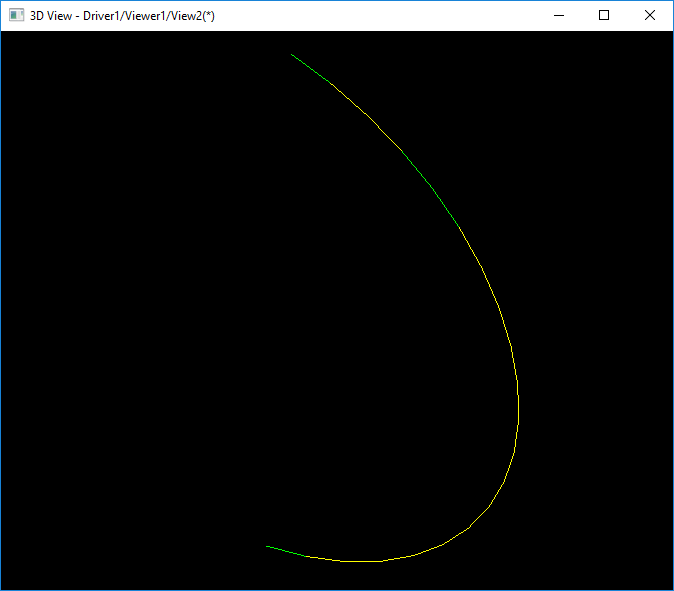
如上圖所示為球面的第一次對(duì)邊界進(jìn)行三角剖分得到的效果。因?yàn)樵谝粋€(gè)參數(shù)上的邊是退化Degenerated邊，所以退化邊的參數(shù)空間上沒(méi)有均分。將參數(shù)空間的三角剖分映射到三維空間后，得到的是一條線，其實(shí)是兩個(gè)非退化邊。
3. Deflection Control
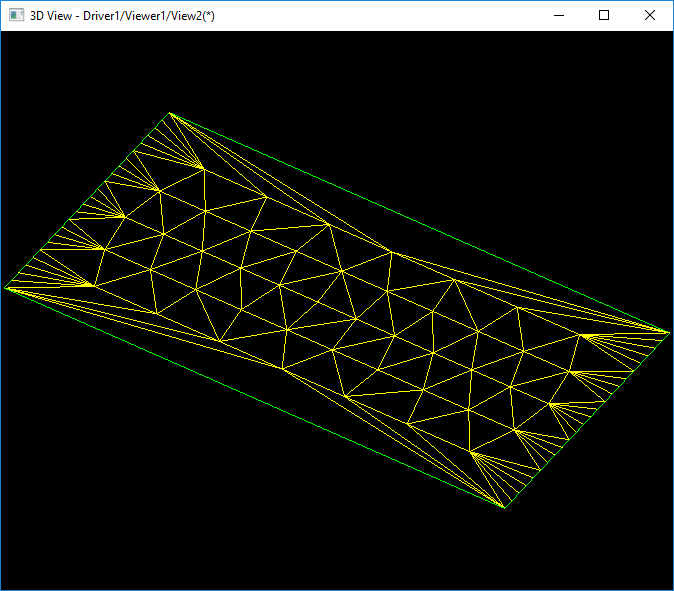
對(duì)于曲面來(lái)說(shuō)，如果直對(duì)邊界進(jìn)行一次三角剖分，是達(dá)不到精度要求。為了使曲面網(wǎng)格剖分效果更好，就需要對(duì)按邊界剖分后的網(wǎng)格進(jìn)行插入點(diǎn)繼續(xù)剖分。對(duì)于上面球面的參數(shù)空間區(qū)域，根據(jù)精度要求插入點(diǎn)剖分后的結(jié)果如下圖所示：
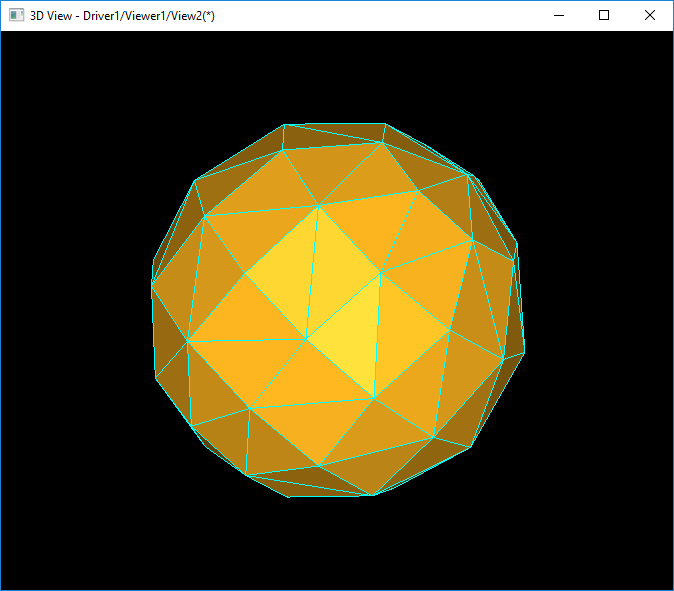
得到的三維效果如下圖所示：
4. Demo
下面給出幾個(gè)自己實(shí)現(xiàn)網(wǎng)格剖分的結(jié)果與OpenCASCADE的TKMesh作個(gè)對(duì)比：
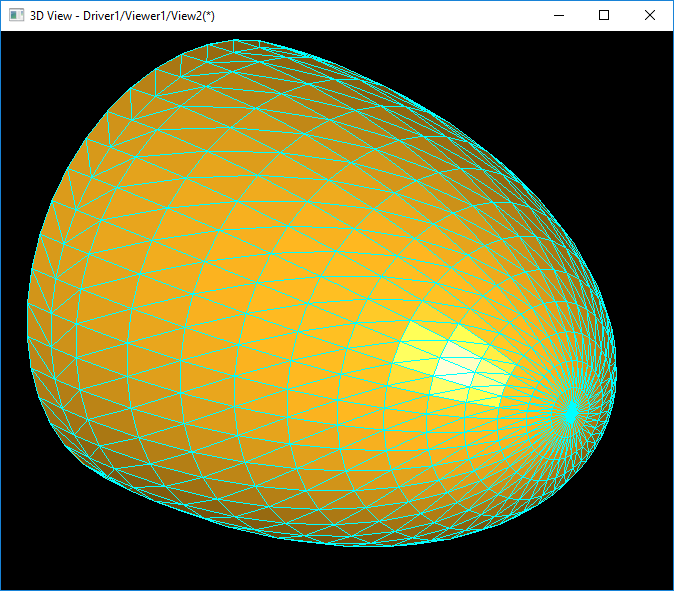
上圖為自己實(shí)現(xiàn)網(wǎng)格剖分算法對(duì)橢球面的網(wǎng)格剖分結(jié)果
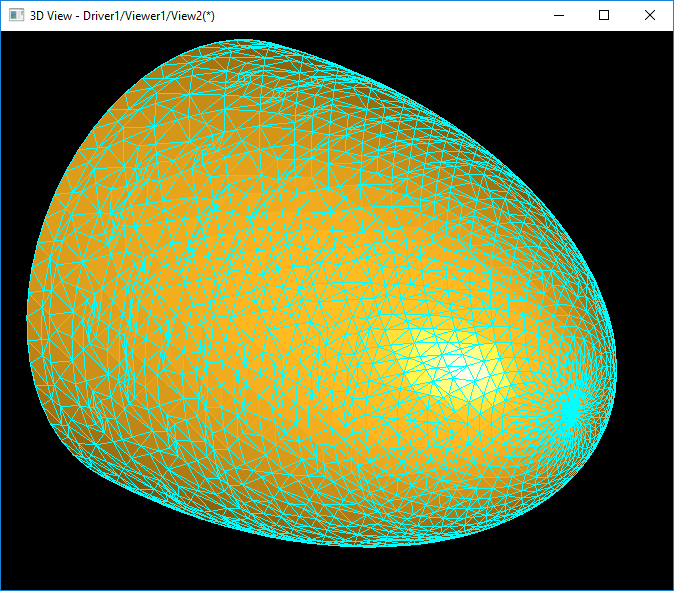
上圖為TKMesh網(wǎng)格剖分算法對(duì)橢球面的網(wǎng)格剖分結(jié)果
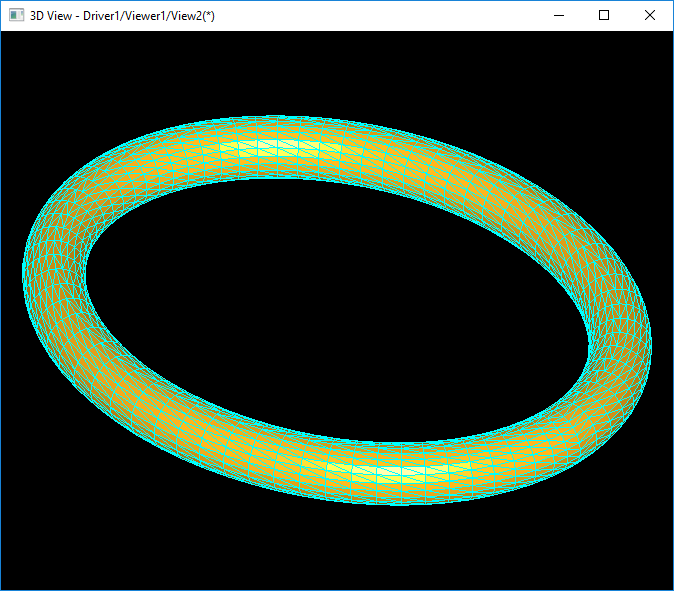
上圖為自己實(shí)現(xiàn)網(wǎng)格剖分算法對(duì)橢圓環(huán)面的網(wǎng)格剖分結(jié)果
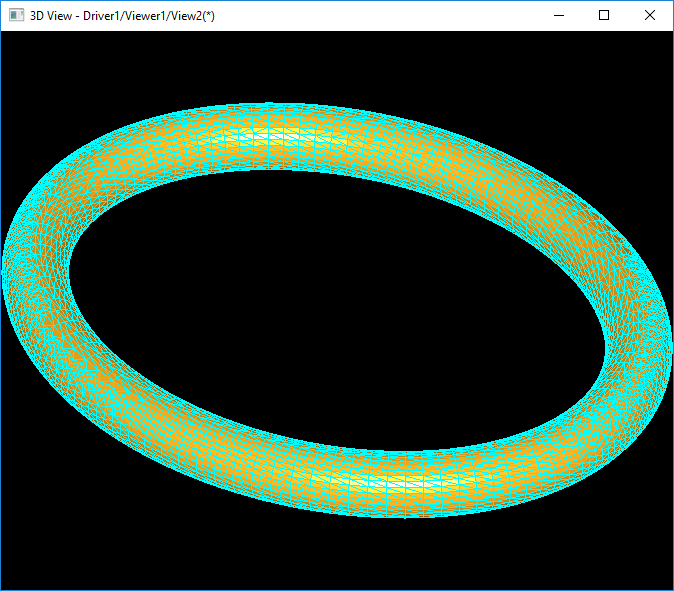
上圖為TKMesh網(wǎng)格剖分算法對(duì)橢圓環(huán)面的網(wǎng)格剖分結(jié)果
通過(guò)上面的對(duì)比可以發(fā)現(xiàn)，在大致相同的顯示效果情況下，OpenCASCADE產(chǎn)生了更多的頂點(diǎn)和三角形數(shù)據(jù)。自己實(shí)現(xiàn)的網(wǎng)格剖分產(chǎn)生的網(wǎng)格質(zhì)量相對(duì)可控且性能高。
5. Conclusion
OpenCASCADE中開源的網(wǎng)格剖分庫(kù)TKMesh可以實(shí)現(xiàn)模型的可視化數(shù)據(jù)生成功能，但是對(duì)于網(wǎng)格剖分的精度可控性差。為了對(duì)模型的網(wǎng)格精度進(jìn)行更好地控制，自己實(shí)現(xiàn)一套網(wǎng)格剖分功能，且性能要優(yōu)于TKMesh。在程序的編寫過(guò)程中，可以加深BREP數(shù)據(jù)結(jié)構(gòu)中一些概念的理解。有興趣的讀者在熟悉BREP數(shù)據(jù)結(jié)構(gòu)后，也可以嘗試下網(wǎng)格剖分功能的實(shí)現(xiàn)。