Intersection between a 2d line and a conic in OpenCASCADE
eryar@163.com
Abstract. OpenCASCADE provides the algorithm to implementation of the analytical intersection between a 2d line and another conic curve. The conic is defined by its implicit quadaratic equation, so the intersection problem is become a polynomial roots finding problem. The paper focus on the 2d line intersection another conic algorithm implementation.
Key Words. 2d line intersection, conic
1.Introduction
高中的時候?qū)W習(xí)了直線Line、圓Circle、圓錐曲線Conic(橢圓Ellipse、雙曲線Hyperbola和拋物線parabola)等二維曲線的方程及特性,也可以對他們之間的相交情況進行計算。如何編程實現(xiàn)直線與任意圓錐曲線相交呢?本文通過對OpenCASCADE中二維直線與圓錐曲線相交代碼的分析來理解其實現(xiàn)原理。
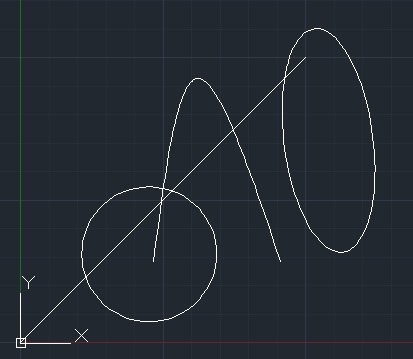
Figure 1. 直線與圓錐曲線相交
對于二維曲線知識的學(xué)習(xí)又把思緒拉回到高中年代,翻開泛黃的課本,遙想那個青澀時候,對于《數(shù)學(xué)》的學(xué)習(xí)也是停留在解題上,沒有理解,更別說應(yīng)用了。有人說數(shù)學(xué)、英語和代碼是當今的世界語言,都可以進行思想的交流。數(shù)學(xué)本來就是描述現(xiàn)實世界規(guī)律的精妙語言,但我終究是個俗人,更崇拜能應(yīng)用數(shù)學(xué)創(chuàng)建價值的人,如OpenCASCADE的開發(fā)者們。
2.Conic Implicit Equation
圓錐曲線一般的代數(shù)表示方法為:
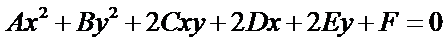
OpenCASCADE中使用類IntAna2d_Conic來表示圓錐曲線的代數(shù)方程。并提供了將二維曲線(直線、圓、橢圓、拋物線、雙曲線)轉(zhuǎn)換成代數(shù)方程的方法,相關(guān)代碼如下所示:
IntAna2d_Conic::IntAna2d_Conic (const gp_Lin2d& L) {
a = 0.0;
b = 0.0;
c = 0.0;
L.Coefficients(d,e,f);
f = 2*f;
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Circ2d& C) {
C.Coefficients(a,b,c,d,e,f);
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Elips2d& E) {
E.Coefficients(a,b,c,d,e,f);
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Parab2d& P) {
P.Coefficients(a,b,c,d,e,f);
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Hypr2d& H) {
H.Coefficients(a,b,c,d,e,f);
}
3.Intersection Implementation
當對直線和圓錐曲線進行求交時,先得到了直線的一般式方程和圓錐曲線的一般式方程,將它們聯(lián)立成方程組如下所示:
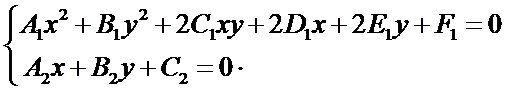
是一個二元二次方程組。通過直線的參數(shù)表示法,將上述二元二次方程組轉(zhuǎn)換成一元二次方程,再對這個方程進行求解。設(shè)直線l經(jīng)過點P0(x0,y0),v=(a, b)是它的一個方向向量。P(x,y)是直線上任意一點,則向量P0P與v共線。根據(jù)向量共線的充要條件,存在唯一實數(shù)t,使:
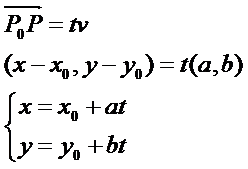
將直線的一般式化為參數(shù)式為:
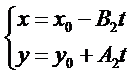
將直線的參數(shù)式代入圓錐曲線的一般式得到:
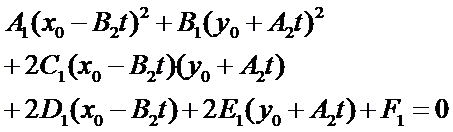
整理上述方程得:
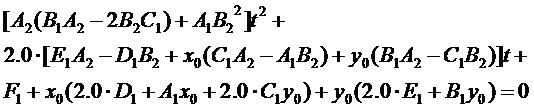
得到各次系數(shù)后,就可以用Newton法來解這個一元二次方程了。OpenCASCADE中的實現(xiàn)代碼如下所示:
void IntAna2d_AnaIntersection::Perform (const gp_Lin2d& L,
const IntAna2d_Conic& Conic)
{
Standard_Real A,B,C,D,E,F;
Standard_Real px0,px1,px2;
Standard_Real DR_A,DR_B,DR_C,X0,Y0;
Standard_Integer i;
Standard_Real tx,ty,S;
done = Standard_False;
nbp = 0;
para = Standard_False;
iden = Standard_False;
Conic.Coefficients(A,B,C,D,E,F);
L.Coefficients(DR_A,DR_B,DR_C);
X0=L.Location().X();
Y0=L.Location().Y();
// Parametre: L
// X = Xo - L DR_B et Y = Yo + L DR_A
px0=F + X0*(D+D + A*X0 + 2.0*C*Y0) + Y0*(E+E + B*Y0);
px1=2.0*(E*DR_A - D*DR_B + X0*(C*DR_A - A*DR_B) + Y0*(B*DR_A - C*DR_B));
px2=DR_A*(B*DR_A - 2.0*C*DR_B) + A*(DR_B*DR_B);
MyDirectPolynomialRoots Sol(px2,px1,px0);
if(!Sol.IsDone()) {
done=Standard_False;
return;
}
else {
if(Sol.InfiniteRoots()) {
iden=Standard_True;
done=Standard_True;
return;
}
nbp=Sol.NbSolutions();
for(i=1;i<=nbp;i++) {
S=Sol.Value(i);
tx=X0 - S*DR_B;
ty=Y0 + S*DR_A;
lpnt[i-1].SetValue(tx,ty,S);
}
Traitement_Points_Confondus(nbp,lpnt);
}
done=Standard_True;
}
從上述源碼可知,OpenCASCADE使用了直線的參數(shù)式來將直線與圓錐曲線的求交表示成一元二次方程,再使用Newton法來對方程進行求解。 其中變量px0、px1、px2分別表示一元二次方程的零次、一次和二次項的系數(shù)。
4.Conclusion
通過圓錐曲線的一般式和直線的參數(shù)式將直線與圓錐曲線相交問題變成一個一元二次方程的求根問題,再通過方程求根的Newton法來對一元二次方程進行求解。
5.References
1. 人民教育出版社中學(xué)數(shù)學(xué)室. 數(shù)學(xué)第二冊上. 人民教育出版社. 2000
2. 易大義, 沈云寶, 李有法. 計算方法. 浙江大學(xué)出版社. 2002
3. 李原, 張開富, 余劍峰. 計算機輔助幾何設(shè)計技術(shù)及應(yīng)用. 西北工業(yè)大學(xué)出版社. 2007
4. 丘維聲. 解析幾何. 北京大學(xué)出版社. 1996