OpenCASCADE Quaternion
eryar@163.com
Abstract. The quaternions are members of a noncommutative division algebra first invented by William Rowan Hamilton. The idea for quaternions occurred to him while he was walking along the Royal Cannal on his way to a meeting of the Irish Academy, and Hamilton was so pleased with his discovery that he scratched the fundamental formula of quaternion algebra. There are several different ways we can express orientation and angular displacement in 3D. Here we discuss the three most important methods-matrices, Euler angles, and quaternions.
Key Words. OpenCASCADE, Quaternion, Euler angles, Rotation, Transformation
1. Introduction
物體在三維空間中經(jīng)常需要進(jìn)行一些變換操作,如移動(dòng)、旋轉(zhuǎn)等。在CAD軟件中如果提供的便利的交互方式來(lái)對(duì)模型的位置進(jìn)行編輯,則軟件的用戶體驗(yàn)就很好。對(duì)模型位置編輯的結(jié)果需要在計(jì)算機(jī)中保存起來(lái),這就需要用一種方式來(lái)記錄模型的變換。如下圖所示:
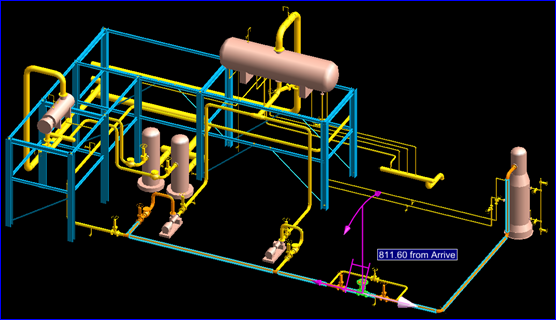
Figure 1.1 Modify the location of a Valve
上圖所示為三維工廠軟件PDMS中使用交互的方式來(lái)修改一個(gè)閥件的位置,直接使用鼠標(biāo)拖動(dòng)高亮的箭頭即可實(shí)現(xiàn)對(duì)閥件位置的編輯。
物體在三維空間中的旋轉(zhuǎn)變換操作常見的有三種表示方法:Matrix、Euler Angles、Quaternion。每種表示方式各用利弊,根據(jù)需要選擇合適的旋轉(zhuǎn)的表示方式。本文詳細(xì)介紹了這三種方式及在OpenCASCADE中使用Quaternion和在這三種表示方式之間進(jìn)行轉(zhuǎn)換。
2.Rotation in Matrix Form
在3D空間中描述坐標(biāo)系的方位(orientation)的一種方法就是列出這個(gè)坐標(biāo)系的基向量,這些基向量是用其他的坐標(biāo)系來(lái)描述的。用這些基向量構(gòu)成一個(gè)3X3矩陣,然后就能用矩陣的形式來(lái)描述方位了。換句話說(shuō),能用一個(gè)旋轉(zhuǎn)矩陣來(lái)描述這兩個(gè)坐標(biāo)系之間的相對(duì)方位,這個(gè)旋轉(zhuǎn)矩陣用于把一個(gè)坐標(biāo)系中的向量變換到另一個(gè)坐標(biāo)系中,如下圖所示:

Figure 2.1 Defining an orientation using a matrix
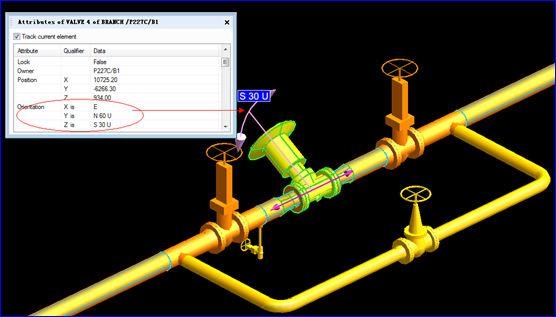
Figure 2.2 A Valve Orientation in PDMS
由上圖可知,在PDMS中對(duì)模型的方位的保存也是采用了矩陣形式,其中X is E,Y is N 60U, Z is S 30 U這其實(shí)是三個(gè)向量。下面給出繞任意軸旋轉(zhuǎn)一定角度的矩陣表示的證明:
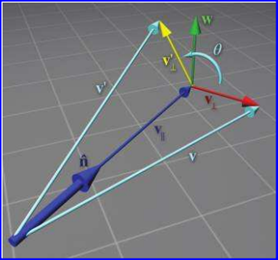
Figure 2.3 Rotating a vector about an arbitrary axis
根據(jù)向量的運(yùn)算規(guī)則容易推出:

則繞軸旋轉(zhuǎn)的矩陣形式如下:
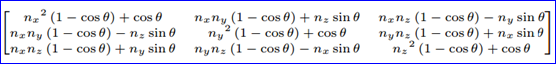
其中在OpenCASCADE的類gp_Mat中實(shí)現(xiàn)代碼如下所示:
void gp_Mat::SetRotation (const gp_XYZ& Axis,
const Standard_Real Ang)
{
// Rot = I + sin(Ang) * M + (1. - cos(Ang)) * M*M
// avec M . XYZ = Axis ^ XYZ
// const Standard_Address M = (Standard_Address)&(matrix[0][0]);
gp_XYZ V = Axis.Normalized();
SetCross (V);
Multiply (sin(Ang));
gp_Mat Temp;
Temp.SetScale (1.0);
Add (Temp);
Standard_Real A = V.X();
Standard_Real B = V.Y();
Standard_Real C = V.Z();
Temp.SetRow (1, gp_XYZ(- C*C - B*B, A*B, A*C ));
Temp.SetRow (2, gp_XYZ( A*B, -A*A - C*C, B*C ));
Temp.SetRow (3, gp_XYZ( A*C, B*C, - A*A - B*B));
Temp.Multiply (1.0 - cos(Ang));
Add (Temp);
}
3.Rotation with Euler Angles
用Euler角的方式來(lái)表示旋轉(zhuǎn)這項(xiàng)技術(shù)是以著名數(shù)學(xué)家Leonhard Euler(1707~1783)來(lái)命名的,他證明了角位移序列等價(jià)于單個(gè)角位移,即可以用一個(gè)合成的變換來(lái)表示多個(gè)連續(xù)的變換,證明過(guò)程詳見蘇步青《應(yīng)用幾何教程》。
Euler Angles的基本思想是將角位移分解為繞三個(gè)互相垂直的三個(gè)旋轉(zhuǎn)組成的序列。這聽起來(lái)有點(diǎn)復(fù)雜,其實(shí)是非常直觀的,這也正是Euler Angle易于使用的優(yōu)點(diǎn)之一。Euler Angle將方位Orientation分解為繞三個(gè)垂直軸的旋轉(zhuǎn),那么是哪三個(gè)軸?按什么順序?其實(shí)任意三個(gè)軸和任意順序都可以,但最有意義的是使用笛卡爾坐標(biāo)系按一定順序所組成的旋轉(zhuǎn)序列。最常用的約定是所謂的“heading-picth-bank”,如下圖所示為給定heading,picth和bank角度后,可以用四步法來(lái)確定Euler Angle對(duì)應(yīng)的Orientation:

Figure 3.1 Step 1: An object in its identity orientation
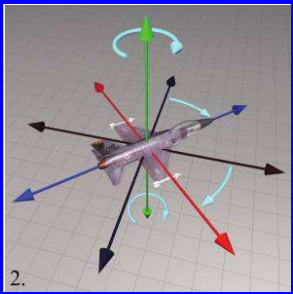
Figure 3.2 Step 2: Heading is the first rotation and rotates about the vertical axis(y-axis)
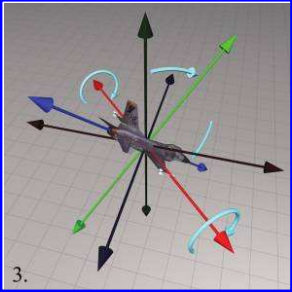
Figure 3.3 Step 3: Pitch is the second rotation and rotates about the object laterial axis(x-axis)
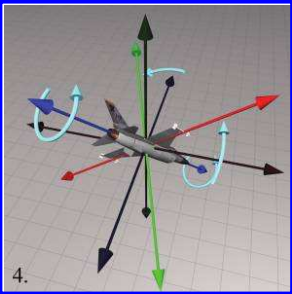
Figure 3.4 Step 4: Bank is the third and rotates about the object longitudinal axis(z-axis)
heading-pitch-bank系統(tǒng)不是唯一的Euler Angle系統(tǒng)。繞任意三個(gè)互相垂直的任意旋轉(zhuǎn)序列都能定義一個(gè)方位orientation。所以多種選擇導(dǎo)致了Euler Angle約定的多樣性。如常用的術(shù)語(yǔ)roll-pitch-yaw,其中roll等價(jià)于bank,yaw基本上等價(jià)于heading,他的順序與heading-pitch-bank相反。
因?yàn)镋uler Angle的易用性,只需要約定旋轉(zhuǎn)序列和三個(gè)角度即可表示方位了。可以仿照上述變換過(guò)程應(yīng)用Euler Angle來(lái)實(shí)現(xiàn)模型旋轉(zhuǎn)編輯的交互操作,實(shí)現(xiàn)交互方式友好的操作。即當(dāng)鼠標(biāo)移動(dòng)到高亮的旋轉(zhuǎn)handle上時(shí),就可以繞一個(gè)軸旋轉(zhuǎn)一定角度,不一定是按heading-pitch-bank的順序來(lái)旋轉(zhuǎn)。如下圖所示:

Figure 5. Model Editor in PDMS

Figure 6. Euler Angle in Model Editor
由上圖可知,對(duì)模型進(jìn)行旋轉(zhuǎn)時(shí),實(shí)時(shí)顯示的角度正是Euler Angle。如果約定了Euler Angle的順序,如為heading-pitch-bank,只需要三個(gè)實(shí)數(shù)即可表示方位orientation,這在將方位數(shù)據(jù)保存到文件時(shí)有很大優(yōu)勢(shì),可以節(jié)省大量存儲(chǔ)空間。如下圖所示:
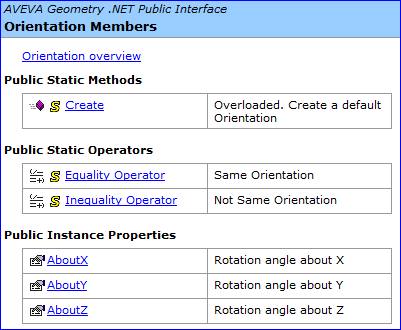
Figure 7. Orientation Properties in AVEVA Plant/PDMS
由上圖可知,PDMS的數(shù)據(jù)庫(kù)中保存orientation的方式使用了Euler Angle的方式,這樣與矩陣的方式相比,數(shù)據(jù)量要少兩倍,因?yàn)橐话愕哪P投加羞@個(gè)屬性,這樣下來(lái),節(jié)省的存儲(chǔ)空間比較可觀。
因?yàn)镋uler Angles的方式最簡(jiǎn)單直觀,就是三個(gè)角度,所以一般都是將Euler Angle轉(zhuǎn)換到其他的形式,如Matrix和Quaternion。
4.Quaternions
一個(gè)Quaternion包含一個(gè)標(biāo)量分量和一個(gè)3D向量分量,一般記標(biāo)量分量為w,向量分量為V或分開的x,y,z,如Q=[w, V]或Q=[w,(x,y,z)]。
Quaternion能被解釋為角位移的軸-角對(duì)方式。然而,旋轉(zhuǎn)軸和角度不是直接存儲(chǔ)在Quaternion的四個(gè)數(shù)中,它們的確在Quaternion中,但是不是那么直接,其關(guān)系式為:
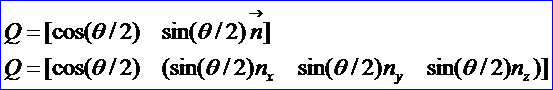
根據(jù)這個(gè)關(guān)系式即可實(shí)現(xiàn)繞軸旋轉(zhuǎn)一定角度的Quaternion,其中OpenCASCADE中的實(shí)現(xiàn)代碼如下所示:
//=======================================================================
//function : SetVectorAndAngle
//purpose :
//=======================================================================
void gp_Quaternion::SetVectorAndAngle (const gp_Vec& theAxis,
const Standard_Real theAngle)
{
gp_Vec anAxis = theAxis.Normalized();
Standard_Real anAngleHalf = 0.5 * theAngle;
Standard_Real sin_a = Sin (anAngleHalf);
Set (anAxis.X() * sin_a, anAxis.Y() * sin_a, anAxis.Z() * sin_a, Cos (anAngleHalf));
}
為了將Quaternion轉(zhuǎn)換到矩陣形式,可以利用繞任意軸旋轉(zhuǎn)的矩陣,公式如下所示:
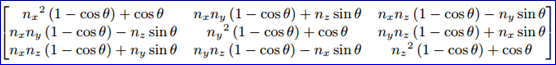
矩陣是由旋轉(zhuǎn)軸n和旋轉(zhuǎn)角度θ表示的,但是Quaternion是由下述分量表示的:
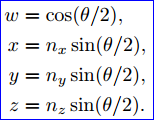
將R(n,θ)變換到R(w,x,y,z)是一個(gè)技巧性很強(qiáng)的推導(dǎo),如果只是為了使用矩陣,那么就不必理解矩陣是如何推導(dǎo)的。如果對(duì)推導(dǎo)過(guò)程感興趣,可參考Fletcher Dunn,Ian Parberry.所著《3D Math Primer for Graphics and Game Development》,其中有詳細(xì)推導(dǎo)說(shuō)明。下面就直接給出推導(dǎo)結(jié)果:
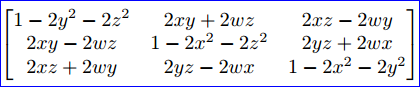
Figure 4.1 Converting a quaternion to a 3x3 matrix
在OpenCASCADE中取得Quaternion的矩陣數(shù)據(jù)是通過(guò)函數(shù)GetMatrix,其實(shí)現(xiàn)代碼如下所示:
//=======================================================================
//function : GetMatrix
//purpose :
//=======================================================================
gp_Mat gp_Quaternion::GetMatrix () const
{
Standard_Real wx, wy, wz, xx, yy, yz, xy, xz, zz, x2, y2, z2;
Standard_Real s = 2.0 / SquareNorm();
x2 = x * s; y2 = y * s; z2 = z * s;
xx = x * x2; xy = x * y2; xz = x * z2;
yy = y * y2; yz = y * z2; zz = z * z2;
wx = w * x2; wy = w * y2; wz = w * z2;
gp_Mat aMat;
aMat (1, 1) = 1.0 - (yy + zz);
aMat (1, 2) = xy - wz;
aMat (1, 3) = xz + wy;
aMat (2, 1) = xy + wz;
aMat (2, 2) = 1.0 - (xx + zz);
aMat (2, 3) = yz - wx;
aMat (3, 1) = xz - wy;
aMat (3, 2) = yz + wx;
aMat (3, 3) = 1.0 - (xx + yy);
// 1 division 16 multiplications 15 addidtions 12 variables
return aMat;
}
由代碼可知,即是對(duì)上述轉(zhuǎn)換公式的直接實(shí)現(xiàn)。如其注釋中所言,轉(zhuǎn)換涉及到了1個(gè)除法、16個(gè)乘法、15個(gè)加法和12個(gè)變量。
OpenCASCADE中還實(shí)現(xiàn)了從Euler Angles轉(zhuǎn)換到Quaternion的功能,實(shí)現(xiàn)代碼如下所示:
//=======================================================================
//function : GetEulerAngles
//purpose :
//=======================================================================
void gp_Quaternion::GetEulerAngles (const gp_EulerSequence theOrder,
Standard_Real& theAlpha,
Standard_Real& theBeta,
Standard_Real& theGamma) const
{
gp_Mat M = GetMatrix();
gp_EulerSequence_Parameters o = translateEulerSequence (theOrder);
if ( o.isTwoAxes )
{
double sy = sqrt (M(o.i, o.j) * M(o.i, o.j) + M(o.i, o.k) * M(o.i, o.k));
if (sy > 16 * DBL_EPSILON)
{
theAlpha = ATan2 (M(o.i, o.j), M(o.i, o.k));
theGamma = ATan2 (M(o.j, o.i), -M(o.k, o.i));
}
else
{
theAlpha = ATan2 (-M(o.j, o.k), M(o.j, o.j));
theGamma = 0.;
}
theBeta = ATan2 (sy, M(o.i, o.i));
}
else
{
double cy = sqrt (M(o.i, o.i) * M(o.i, o.i) + M(o.j, o.i) * M(o.j, o.i));
if (cy > 16 * DBL_EPSILON)
{
theAlpha = ATan2 (M(o.k, o.j), M(o.k, o.k));
theGamma = ATan2 (M(o.j, o.i), M(o.i, o.i));
}
else
{
theAlpha = ATan2 (-M(o.j, o.k), M(o.j, o.j));
theGamma = 0.;
}
theBeta = ATan2 (-M(o.k, o.i), cy);
}
if ( o.isOdd )
{
theAlpha = -theAlpha;
theBeta = -theBeta;
theGamma = -theGamma;
}
if ( ! o.isExtrinsic )
{
Standard_Real aFirst = theAlpha;
theAlpha = theGamma;
theGamma = aFirst;
}
}
下面給出在OpenCASCADE中使用Quaternion的具體示例,代碼如下所示:
/*
* Copyright (c) 2013 to current year. All Rights Reserved.
*
* File : Main.cpp
* Author : eryar@163.com
* Date : 2014-11-29 10:18
* Version : OpenCASCADE6.8.0
*
* Description : Test OpenCASCADE quaternion.
*
* Key Words : OpenCASCADE, Quaternion
*
*/
#define WNT
#include <gp_Quaternion.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
void TestQuaternion(void)
{
gp_Quaternion aQuaternion;
// create quaternion by axis-angle.
aQuaternion.SetVectorAndAngle(gp_Vec(1.0, 0.0, 0.0), M_PI_2);
// convert quaternion to matrix.
gp_Mat aMatrix = aQuaternion.GetMatrix();
Standard_Real aYaw = 0.0;
Standard_Real aPitch = 0.0;
Standard_Real aRoll = 0.0;
// convert quaternion to Euler Angles.
aQuaternion.GetEulerAngles(gp_YawPitchRoll, aYaw, aPitch, aRoll);
}
int main(int argc, char* argv[])
{
TestQuaternion();
return 0;
}
5.Conclusions
綜上所述,Euler Angles最容易被使用,當(dāng)需要為世界中的物體指定方位時(shí),Euler Angles能大簡(jiǎn)化人機(jī)交互,包括直接的鍵盤、鼠標(biāo)輸入及在調(diào)試中測(cè)試。
如果需要要坐標(biāo)系之間進(jìn)行轉(zhuǎn)換向量,那么就選矩陣形式。當(dāng)然這并不意味著你不能使用其他格式來(lái)保存方位,并在需要的時(shí)候轉(zhuǎn)換到矩陣形式。另一種方法是用Euler Angles作為方位的“主拷貝”,并同時(shí)維護(hù)一個(gè)旋轉(zhuǎn)矩陣,當(dāng)Euler Angles發(fā)生變化時(shí)矩陣也同時(shí)進(jìn)行更新。
當(dāng)需要大量保存方位數(shù)據(jù)時(shí),就使用Euler Angles或Quaternion。Euler Angles將少占用25%的空間,但它在轉(zhuǎn)換到矩陣時(shí)要稍微慢點(diǎn)。如果動(dòng)畫數(shù)據(jù)需要進(jìn)行坐標(biāo)系之間的連接,Quaternion可能是最好的選擇了。
平滑的插值只能用Quaternion來(lái)完成,這在OpenSceneGraph中有大量的應(yīng)用。如果你使用其他形式,也可先轉(zhuǎn)換成Quaternion再進(jìn)行插值,插值完成后再轉(zhuǎn)換回原來(lái)的形式。
OpenCASCADE的Quaternion類中實(shí)現(xiàn)了Matrix, Euler Angles的轉(zhuǎn)換,即通過(guò)gp_Quaternion即可將旋轉(zhuǎn)操作在這三種形式之間進(jìn)行轉(zhuǎn)換。
6. References
1. WolframMathWorld, http://mathworld.wolfram.com/Quaternion.html
2. Ken Shoemake. Conversion between quaternion and Euler angles. Graphics Gems IV, P222-22
http://tog.acm.org/resources/GraphicsGems/gemsiv/euler_angle/EulerAngles.c
3. 蘇步青, 華宣積. 應(yīng)用幾何教程. 復(fù)旦大學(xué)出版計(jì). 2012
4. 丘維聲. 解析幾何. 北京大學(xué)出版社. 1996
5. 同濟(jì)大學(xué)應(yīng)用數(shù)學(xué)系編. 線性代數(shù)(第四版). 高等教育出版社. 2003
6. Fletcher Dunn,Ian Parberry. 3D Math Primer for Graphics and Game Development. CRC Press
7. 史銀雪,陳洪,王榮靜. 3D數(shù)學(xué)基礎(chǔ):圖形與游戲開發(fā). 清華大學(xué)出版社. 2005
8. 蘇步青. 神奇的符號(hào). 湖南少年兒童出版社. 2010