OpenCASCADE Conic to BSpline Curves-Circle
eryar@163.com
Abstract. The conic sections and circles play a fundamental role in CAD/CAM applications. Undoubtedly one of the greatest advantages of NURBS is their capability of precisely representing conic sections and circles, as well as free-form curves and surfaces. We assume a knowledge of conics and circles, the purpose of this paper is to study them in the framework of their representation as NURBS curves.
Key Words. OpenCASCADE, Conic Curves, Circle, Convert, BSpline Curve
1. Introduction
B樣條技術(shù)在自由曲線曲面的設(shè)計和表示方面顯示出了其卓越的優(yōu)點，但在表示初等曲線曲面時卻遇到了麻煩。在很多應(yīng)用領(lǐng)域，例如飛機、造船、汽車等工業(yè)中，圓弧、橢圓弧、拋物線、圓柱面、球面、圓錐面、圓環(huán)面等經(jīng)常出現(xiàn)，這些形狀都表示精確且往往要求較高的加工精度。傳統(tǒng)的B樣條技術(shù)只能精確地表示拋物線、拋物面，對其他的二次曲線曲面只能近似表示。因此，在一個造型系統(tǒng)內(nèi)無法用一種統(tǒng)一的形式表示曲線曲面，因而使得系統(tǒng)的開發(fā)復(fù)雜化。非均勻有理B樣條（NURBS）技術(shù)正是在這樣的需求背景下逐步發(fā)展成熟起來的。
NURBS曲線曲面能夠迅速接受的主要原因在于：
v NURBS技術(shù)可以精確表示規(guī)則曲線與曲面（如圓錐曲線、二次曲面、旋轉(zhuǎn)曲面等）。
v 可以把規(guī)則曲線曲面和自由曲線曲面統(tǒng)一起來表示。因而便于用統(tǒng)一的算法進行處理和使用統(tǒng)一的數(shù)據(jù)庫進行存儲，程序量可明顯減少；
v 由于增加了額外的自由度（權(quán)因子），若應(yīng)用得當(dāng)，有利于曲線曲面形狀的控制和修改。
v NURBS技術(shù)是非有理Bezier曲線的和B樣條形式的真正推廣；
本文主要介紹圓的NURBS表示方法，即如何將圓轉(zhuǎn)換為NURBS曲線。
2.The Effect of Multiple Knots (Multiplicity)
重節(jié)點的定義為在節(jié)點序列中順序r個節(jié)點相同或xi重復(fù)出現(xiàn)r次，稱為該節(jié)點xi具有重復(fù)度r（Multiplicity）。在OpenCASCADE中B樣條曲線類的構(gòu)造就是用的節(jié)點Knots及其對應(yīng)的重復(fù)度Multiplicities來實現(xiàn)的，如下所示：
//! Creates a non-rational B_spline curve on the <br>
//! basis <Knots, Multiplicities> of degree <Degree>. <br>
Standard_EXPORT Geom_BSplineCurve(const TColgp_Array1OfPnt& Poles,const TColStd_Array1OfReal& Knots,const TColStd_Array1OfInteger& Multiplicities,const Standard_Integer Degree,const Standard_Boolean Periodic = Standard_False);
重節(jié)點有如下重要性質(zhì)：
v 重節(jié)點連續(xù)階性質(zhì)。在每個節(jié)點區(qū)間(uj, uj+1)內(nèi)部，Bi,p(u)為多項式函數(shù)，因此，所有導(dǎo)數(shù)存在。在一個節(jié)點uj處Bi,p(u)是p-mj次連續(xù)可微的，此處mj是該點的重數(shù)。所以增加次數(shù)，則增加連續(xù)性，而增加節(jié)點的重數(shù)，則降低連續(xù)性。通常為保證連續(xù)性，節(jié)點的最高重數(shù)為p；
v 重節(jié)點的插值基函數(shù)性質(zhì)。當(dāng)節(jié)點向量中的內(nèi)節(jié)點uj的重數(shù)為p，則只有定義在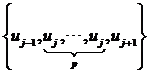
上的基函數(shù)在uj上取值為1，其余基函數(shù)在uj取值為0。當(dāng)節(jié)點向是中的端節(jié)點uj的重數(shù)為p+1，則只有定義在
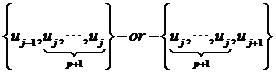上的基函數(shù)在uj取值為1，其余基函數(shù)在uj取值為0。
如下圖所示為具有重節(jié)點的B樣條基函數(shù)：
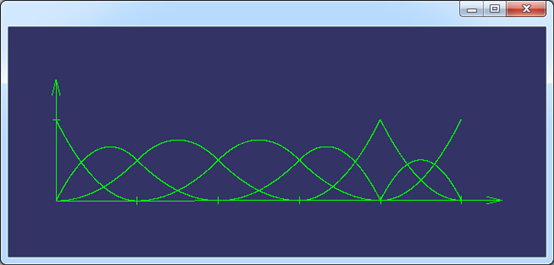
Figure 2.1 U={0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5} p = 2 B-spline Basis Function
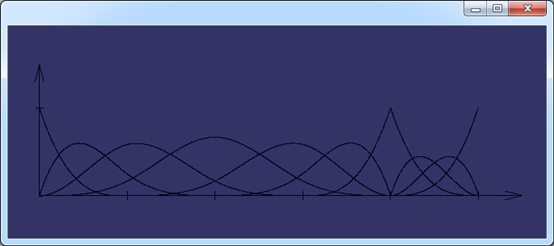
Figure 2.2 U={0, 0, 0, 0,1, 2, 3, 4, 4,4, 5, 5, 5,5} p = 3 B-spline Basis Function
由上圖可知，重節(jié)點的出現(xiàn)對B樣條曲線有影響，如下所述：
當(dāng)節(jié)點向量內(nèi)部某節(jié)點的重數(shù)與次數(shù)相同時，則B樣條基數(shù)在此節(jié)點處的值為1，即由此得到的B樣條曲線的控制頂點將與B樣條曲線上的點重合。所以利用重節(jié)點的插值性質(zhì)可以在B樣條曲線內(nèi)部構(gòu)造尖點與尖角。
當(dāng)端節(jié)點重數(shù)為p時，p次的B樣條曲線的端點將與相應(yīng)的控制多邊形的端點相重，曲線在端節(jié)點處與控制多邊形相切。
當(dāng)端節(jié)點重數(shù)為p+1時，p次B樣條曲線就具有與p次Bezier曲線相同的端點幾何性質(zhì)。這時如果B樣條曲線的定義域僅有一個非零節(jié)點區(qū)間，則所定義的B樣條曲線就是Bezier曲線。由此可知，B樣條方法是Bezier方法的強有力的推廣。
理解重節(jié)點的作用非常重要，利用重節(jié)點技術(shù)可用來控制B樣條基以達到控制整條曲線在節(jié)點處的連續(xù)性的目的。
3.Construction of Circles
如前所述，NURBS技術(shù)是Bezier技術(shù)的推廣。實際上，有理Bezier技術(shù)就可精確地表示圓錐曲線。由有理Bezier曲線的公式得二次有理Bezier曲線弧的表示形式為：
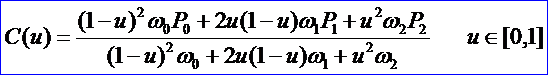
稱k為形狀不變因子，公式如下所示：
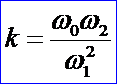
一段小于180度的圓弧也可以用二次有理Bezier曲線來表示。由于對稱性，P0P1P2必須是一個等腰三角形，滿足P0P1=P1P2，計算得ω1＝cos(θ)。
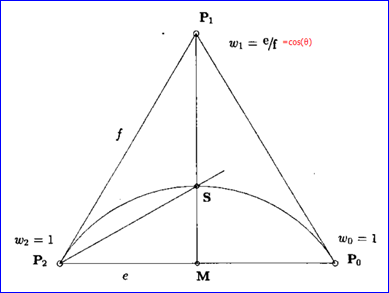
Figure 3.1 圓心角度小于180度圓弧的二次有理Bezier表示
大于180度的圓弧可以使用多段小圓弧拼接而成。得用重節(jié)點技術(shù)，使多段圓弧拼接起來。重節(jié)點的一種方法是使用2重節(jié)點，在有i段圓弧時，其內(nèi)部節(jié)點值可取為1/i，…，i-1/i，權(quán)因子的取法不變。
以180度的圓弧為例，可以使用兩段90度圓弧拼接而成。節(jié)點矢量可取為U＝{0，0，0，1/2，1/2，1，1，1}。權(quán)因子可以取為ω1＝ω3＝cos45，ω0＝ω2＝ω4＝1。則對應(yīng)的B樣條基函數(shù)及B樣條曲線如下圖所示：
由圖可知基函數(shù)在1/2處取值為1，則對應(yīng)的B樣條曲線上的值與控制頂點重合。
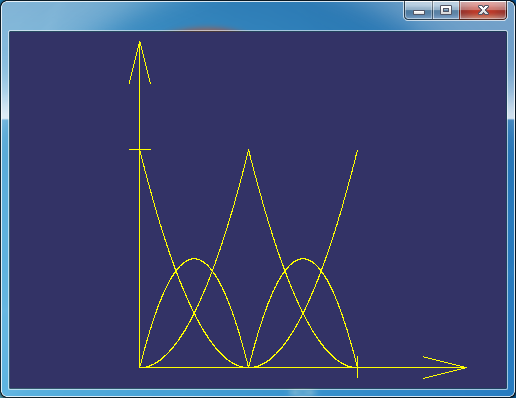
Figure 3.2 U＝{0，0，0，1/2，1/2，1，1，1} B Spline Basis
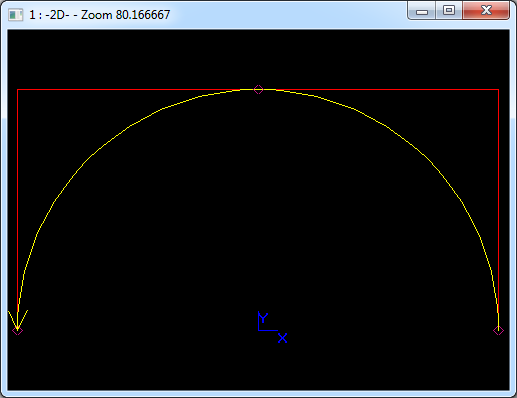
Figure 3.3 Semi-Circle B Spline Curve
用四段圓弧組成一個整圓，節(jié)點矢量為U＝{0，0，0，1/4，1/4，2/4，2/4，3/4，3/4，1，1，1}，權(quán)因子取{1，sqrt(2)/2，1，1，sqrt(2)/2，1，1，sqrt(2)/2，1}，使用Tcl腳本在Draw Test Harness中顯示如下圖所示：
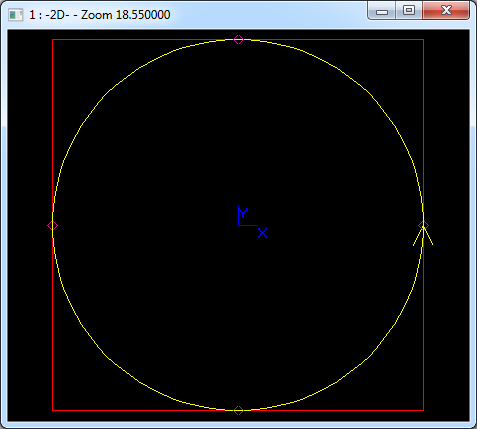
Figure 3.4 A Circle represented by 4 arcs
Tcl代碼如下所示：
#
# Copyright (c) 2014 eryar All Rights Reserved.
#
# File : colorscale.tcl
# Author : eryar@163.com
# Date : 2014-10-13 18:10
# Version : 1.0v
#
# Description : Demonstrate the rational 2d Bezier curve
# and BSpline curve.
#
pload MODELING
# use 4 arc to composite a circle
2dbsplinecurve c2 2 \
5 0 3 1/4 2 2/4 2 3/4 2 1 3 \
10 0 1 \
10 10 sqrt(2.0)/2.0 \
0 10 1 \
-10 10 sqrt(2.0)/2.0 \
-10 0 1 \
-10 -10 sqrt(2.0)/2.0 \
0 -10 1 \
10 -10 sqrt(2.0)/2.0 \
10 0 1
# fit the 2d view
v2d
2dfit
也可用位于三角形上的控制點來表示圓，如下圖所示：
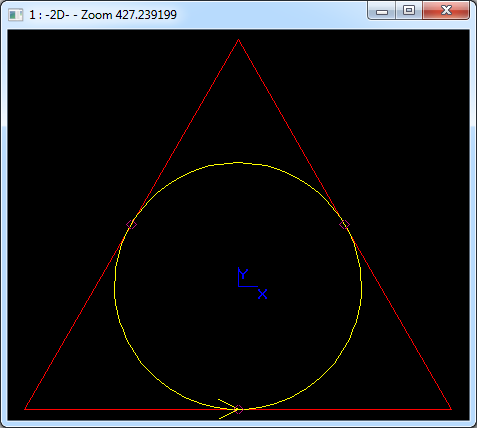
Figure 3.5 A Circle represented by 3 arcs
相應(yīng)的Tcl代碼如下所示：
pload MODELING
# a 2d periodic circle (parameter from 0 to 2*pi !!)
dset h sqrt(3)/2
2dpbsplinecurve c3 2 \
4 0 2 pi/1.5 2 pi/0.75 2 2*pi 2 \
0 -h/3 1 \
0.5 -h/3 0.5 \
0.25 h/6 1 \
0 2*h/3 0.5 \
-0.25 h/6 1 \
-0.5 -h/3 0.5 \
0 -h/3 1
# fit the 2d view
v2d
2dfit
4.Code Analysis
OpenCASCADE中提供了將圓轉(zhuǎn)換為NURBS曲線的功能，轉(zhuǎn)換后得到的NURBS曲線的參數(shù)范圍不再是[0，1]。下面給出具體的實例：
void TestCircleConvert(void)
{
gp_Circ2d aCircle;
aCircle.SetRadius(1.0);
Convert_ParameterisationType aType = Convert_TgtThetaOver2;
Convert_CircleToBSplineCurve aConvertor(aCircle, aType);
Handle_Geom_Circle aGeomCircle = GC_MakeCircle(gp::XOY(), 1.0);
Handle_Geom_BSplineCurve aBSplineCurve =
GeomConvert::CurveToBSplineCurve(aGeomCircle, aType);
std::cout << "Convert Circle to BSpline Curve: " << std::endl;
DumpConvertorInfo(aConvertor);
}
int main(int argc, char* argv[])
{
TestCircleConvert();
return 0;
}
結(jié)果如下圖所示：
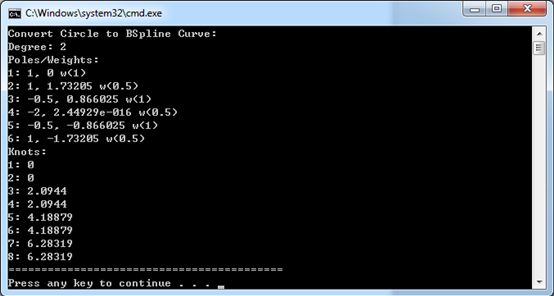
由上述結(jié)果可知，在默認參數(shù)化的情況下是按三段圓弧來拼接成一個整圓的。也可指定不同的參數(shù)化類型，將會得到不同的NURBS曲線。次數(shù)也可能不是2次，會用高次的NURBS曲線來表示圓。
5.Conclusion
利用重節(jié)點技術(shù)及二次有理B樣條的性質(zhì)，可以用NURBS來精確表示圓。選擇不同的控制頂點，得到的圓的參數(shù)化效果也有所不同。
將常用的圓錐曲線用NURBS曲線來表示，即說明可以用NURBS曲線來統(tǒng)一表示圓錐曲線及自由曲線。這說明在理論上，一個造型內(nèi)核的曲線可以只用一個類來表示，這個類對應(yīng)OpenCASCADE中的Geom_BSplineCurve。
使用Tcl可以在Draw Test Harness中方便地產(chǎn)生NURBS曲線，從而可以快速驗證一些算法的正確性。
6. References
1． 趙罡，穆國旺，王拉柱譯Les Piegl，Wayne Tiller The NURBS Book(Second Edition) 2010 清華大學(xué)出版社
2． 莫容，常智勇 計算機輔助幾何造型技術(shù) 2009 科學(xué)出版社
3． 朱心雄等，自由曲線曲面造型技術(shù)，2000，科學(xué)出版社
4． Kelly Dempski, Focus on Curves and Surface, 2003, Premier Press
5． 王仁宏，李崇君，朱春鋼 計算幾何教程 2008 科學(xué)出版社