OpenCASCADE Conic to BSpline Curves-Parabola
eryar@163.com
Abstract. Rational Bezier Curve can represent conic curves such as circle, ellipse, hyperbola, .etc. But how to convert a conic curve to BSpline curve is still question, i.e. Represent a conic curve in BSpline form. Parabola curve is the most simple conic curve, that the parabola does not require rational functions. Let’s begin from the simplest one...
Key Words. OpenCASCADE, Convert, Parabola, BSplineCurve, Conic Curve
1. Introduction
圓錐截線(Conic或稱為二次曲線)和圓在CAD/CAM中有著廣泛應用。毫無疑問NURBS的一個最大優點就是既能精確表示圓錐截線和圓,也能精確表示自由曲線曲面。這個優點的意義是方便編程,使所有的曲線可以采用統一的數據結構來表示。通過有理的方式可以精確來表示這些二次曲線,那么給定一個二次曲線的相關參數(如圓的圓心和半徑等),如何構造出對應的NURBS曲線呢?
在圓錐截線中,拋物線(Parabola)是不需要用有理函數來表示的,所以是形式最簡單的二次曲線。先從簡單的著手,來學習如何將一個拋物線從隱式方程的形式轉換成NURBS曲線形式。
先簡要回顧一下高中數學中關于拋物線的相關知識點,如下圖所示為我上高中時數學課本中的關于拋物線方程及焦點坐標(focus)和準線(directrix)方程一個圖表:

Figure 1.1 Parabola Fuction
OpenCASCADE中對應拋物線的隱式方程表示的類是gp_Parab/gp_Parab2d。本文主要介紹OpenCASCADE中如何將gp_Parab2d轉換為NURBS曲線。
2. Parametric Representations
在CAD/CAM的應用中,圓錐截線有兩種重要的參數表示形式:有理形式和最大內接面積形式(Rational and maximum inscribed area forms)。表示拋物線的這兩種形式是相同的,如下所示:

圓錐截線的有些有理參數表示形式可能是有相當差的參數化,即均勻分布的參數值對應于曲線上分布很不均勻的點。利用線性有理函數對有理曲線進行重新參數化可以改變(因而可能改善)其參數化。
假設C(u)=(x(u), y(u))是一條在標準位置的圓錐截線的參數表示。現在我們對拋物線給出的參數方程也是上式,它是一個好的參數化:對于任意給定的整數n和參數邊界a與b,取n個等間隔分布的參數:

點C(u1),C(u2), ..., C(un)形成曲線上n-1邊多邊形,它的閉合多邊形具有最大的內接面積。
根據最大內接面積表示法可以求出節點矢量。
3. Conversion Algorithm
將隱式表示的拋物線方程轉換為NURBS(有理Bezier是NURBS的特例)曲線需要確定NURBS的以下信息:節點矢量,權因子,次數,控制頂點。
因為拋物線是二次曲線,所以對應的NURBS曲線的次數也為2。因為是用有理的Bezier曲線來表示的,所以需要的控制頂點數為3。
其中節點矢量可由最大內接面積表示法來確定。下面來確定剩余的所需數據。由有理Bezier曲線的公式得二次有理Bezier曲線弧的表示形式為:
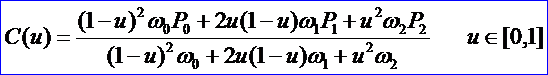
稱k為形狀不變因子,公式如下所示:
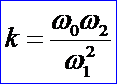
可以證明同一組控制頂點選取不同 的權因子,只要形狀因子k相等,則由它們決定的二次有理Bezier曲線是同一條曲線段,不同的權因對應不同的參數化,而且可以根據形狀不變因子對二次曲線進行分類:
v K=0; 表示退化的二次曲線:一對直線段P0P1和P1P2;
v K∈[0,1]; 表示雙曲線;
v K=1; 表示拋物線;
v K∈[1, +∞]; 表示橢圓;
v K=+∞; 表示連接P0和P2的直線段;
習慣上我們選擇ω0=ω2=1稱為標準參數化。此時由形狀因子k公式得拋物線的ω1=1。所以拋物線的權因子也因此而確定,即ω0=ω1=ω2=1。

Figure 3.1 不同的權因子ω1 定義的圓錐截線
由二次有理Bezier曲線公式可知,當u=0和u=1時,C(0)=P0, C(1)=P2,即曲線通過特征多邊形的首末頂點。由此可確定拋物線的兩個控制頂點P0和P2,現在只剩下最后一個P1頂點未確定。
P1點可以由二次有理Bezier曲線的公式列方程計算得出,但這并不是一個方便的方法。一種更方便的方法是:在這條曲線上指定第三個點,該點對應于某個特定的參數,例如u=1/2。點S=C(1/2)稱為圓錐截線的肩點(shoulder point),如圖3.1所示。將u=1/2代入二次有理Bezier公式得:

其中M是弦P0P2的中點。肩點S=C(1/2)。所以由上式可確定P1點。下面將各個控制頂點的計算列出如下所示:
設拋物線的起止區間為[UF,UL],則因為曲線通過特征多邊形的頂點,所以通過首點P0=(X0,Y0)=(X0,UF)。又由拋物線的參數方程可知:

同理可計算出通過末點P2的坐標,將他們分別列出如下:

由計算肩點S的公式,將Sy=Y1=C(u1)=(UF+UL)/2代入可得:

所以P1點的坐標為:

至此,拋物線的三個控制頂點P0,P1,P2都已計算出來了。即拋物線的NURBS表示所需的數據都已經得到了。下面看看OpenCASCADE中的實現代碼。
4. Code Analysis
OpenCASCADE的Math工具集中有個包Covert用來將圓錐曲線曲面轉換為NURBS曲線曲面。其中轉換拋物線的類為:Convert_ParabolaToBSplineCurve,實現代碼如下所示:
//=======================================================================
//function : Convert_ParabolaToBSplineCurve
//purpose :
//=======================================================================
Convert_ParabolaToBSplineCurve::Convert_ParabolaToBSplineCurve
(const gp_Parab2d& Prb,
const Standard_Real U1 ,
const Standard_Real U2 )
: Convert_ConicToBSplineCurve (MaxNbPoles, MaxNbKnots, TheDegree)
{
Standard_DomainError_Raise_if( Abs(U2 - U1) < Epsilon(0.),
"Convert_ParabolaToBSplineCurve");
Standard_Real UF = Min (U1, U2);
Standard_Real UL = Max( U1, U2);
Standard_Real p = Prb.Parameter();
nbPoles = 3;
nbKnots = 2;
isperiodic = Standard_False;
knots->ChangeArray1()(1) = UF; mults->ChangeArray1()(1) = 3;
knots->ChangeArray1()(2) = UL; mults->ChangeArray1()(2) = 3;
weights->ChangeArray1()(1) = 1.;
weights->ChangeArray1()(2) = 1.;
weights->ChangeArray1()(3) = 1.;
gp_Dir2d Ox = Prb.Axis().XDirection();
gp_Dir2d Oy = Prb.Axis().YDirection();
Standard_Real S = ( Ox.X() * Oy.Y() - Ox.Y() * Oy.X() > 0.) ? 1 : -1;
// poles expressed in the reference mark
poles->ChangeArray1()(1) =
gp_Pnt2d( ( UF * UF) / ( 2. * p), S * UF );
poles->ChangeArray1()(2) =
gp_Pnt2d( ( UF * UL) / ( 2. * p), S * ( UF + UL) / 2. );
poles->ChangeArray1()(3) =
gp_Pnt2d( ( UL * UL) / ( 2. * p), S * UL );
// replace the bspline in the mark of the parabola
gp_Trsf2d Trsf;
Trsf.SetTransformation( Prb.Axis().XAxis(), gp::OX2d());
poles->ChangeArray1()(1).Transform( Trsf);
poles->ChangeArray1()(2).Transform( Trsf);
poles->ChangeArray1()(3).Transform( Trsf);
}
由上面的代碼可知,先設置曲線次數為2,再設置節點矢量為[UF,UF,UF,UL,UL,UL],即首參數UF和末參數UL的重數皆為3,由節點矢量可知轉換后的NURBS曲線為Bezier曲線。
三個控制頂點對應的權因也都設置為1。三個控制頂點計算方法按上一節中所述。關鍵是P1點的計算。上面的計算方法僅為個人觀點,歡迎討論交流。
最后根據有理Bezier曲線的仿射不變性:對有理Bezier曲線進行旋轉、平移和縮放變換,其表達式不變,只是控制點發生了改變。新的控制點可以通過對原控制點作變換得到。即要對有理Bezier曲線進行仿射變換,只需對其控制點作變換即可。
圓錐截線的轉換類的使用是很簡單的,且計算都是在構造函數中完成。下面給出一個將拋物線轉換為NURBS曲線的具體示例來說明其用法。
/*
* Copyright (c) 2014 eryar All Rights Reserved.
*
* File : Main.cpp
* Author : eryar@163.com
* Date : 2014-10-02 20:46
* Version : 1.0v
*
* Description : OpenCASCADE conic to BSpline curve-Parabola.
*
* Key words : OpenCascade, Parabola, BSpline Curve, Convert
*/
#define HAVE_CONFIG_H
#include <gp_Parab2d.hxx>
#include <Convert_ParabolaToBSplineCurve.hxx>
void DumpConvertorInfo(const Convert_ConicToBSplineCurve &theConvertor)
{
Standard_Integer aCounter = 0;
std::cout << "Convert Result" << std::endl;
std::cout << "Degree: " << theConvertor.Degree() << std::endl;
std::cout << "Periodic: " << (theConvertor.IsPeriodic() ? "yes" : "no") << std::endl;
std::cout << "Knots: " << std::endl;
for (Standard_Integer i = 1;i <= theConvertor.NbKnots(); ++i)
{
for (Standard_Integer j = 1; j <= theConvertor.Multiplicity(i); ++j)
{
std::cout << ++aCounter << ": " << theConvertor.Knot(i) << std::endl;
}
}
std::cout << "Poles(Weight): " << std::endl;
for (Standard_Integer i = 1; i <= theConvertor.NbPoles(); ++i)
{
gp_Pnt2d aPole = theConvertor.Pole(i);
std::cout << i << ": " << aPole.X() << ", " << aPole.Y()
<< " W(" << theConvertor.Weight(i) << ")" << std::endl;
}
}
void TestParabolaConversion(void)
{
gp_Parab2d aParabola(gp::OX2d(), 1.0);
Convert_ParabolaToBSplineCurve aConvertor(aParabola, 1.0, M_PI);
DumpConvertorInfo(aConvertor);
}
int main(int argc, char **argv)
{
TestParabolaConversion();
return 0;
}
程序開始部分需要定義HAVE_CONFIG_H,這與在Windows中編程定義WNT有所不同。程序輸出結果如下圖所示:

Figure 4.1 Convert Parabola to BSpline Curve Result
5. Conclusion
NURBS的一個優勢就是統一了曲線曲面的表示方法,即不僅可以表示自由曲線曲面,還可精確表示圓錐曲線曲面。其中拋物線是最簡單的圓錐截線,從簡單的拋物線轉換成NURBS曲線著手,學習NURBS是如何來表示圓錐截線的。
第一次使用Debian系統來編程,選用了一個輕量級的IDE開發工具Codelite,用法與Visual Studio類似。期間也遇到包含引用目錄及程序運行時找不到動態庫的問題。其中在Codelite中添加引用庫路徑的方法如下圖所示:

Figure 5.1 Set Library Path and Add Libraries in Codelite
添加上述引用庫后,解決了鏈接錯誤,但是直接運行程序,發現也有與在Windows中類似的問題,即缺少依賴的動態庫,如下圖所示為使用lld命令檢查程序的依賴項。最后通過向ld.so.conf中添加動態庫所在的目錄解決了問題。相關命令如下所示:
# cat /etc/ld.so.conf
include ld.so.conf.d/*.conf
# echo "/home/eryar/opencascade-6.7.1/lib" >> /etc/ld.so.conf
# ldconfig
注:以上命令需要有root權限。

Figure 5.2 Use lld command to check depends
通過解決以上的問題,來適應在Debian中使用Codelite開發程序。
6. References
1. 人民教育出版社中學數學室. 數學第二冊(上). 人民教育出版社. 2000
2. 趙罡,穆國旺,王拉柱譯. 非均勻有理B樣條. 清華大學出版社. 2010
3. 王仁宏,李崇君,朱春鋼. 計算幾何教程. 科學出版社. 2008