OpenCascade B-Spline Basis Function
eryar@163.com
Abstract. B-splines are quite a bit more flexible than Bezier curves. This flexibility comes from the fact that you have much more control over the basis functions. For Bezier curves that each control point had an effect on each point on the curve; likewise the number of control points affected the degree of the curve. For the sake of flexiblity, you would like to be able to arbitrarily set the degree of the curve and to also determine the range of the affect each control point has. B-splines allow this level of control, the secret is its basis function. This paper focus on the B-splines basis function and some important properties of B-spline basis function, such as local support property, the multiplicity of the knot vector .etc.
Key words. B-spline Basis Function, OpenCascade B-spline, Multiplicity,
1. Introduction
在當前的CAD/CAM系統中,B樣條曲線曲面已經成為幾何造型系統的核心部分。B樣條曲線曲面造型方法的理論基礎就是B樣條。Bezier曲線是以Bernstein基函數為基礎的,雖然它有許多優點,但也有一些不足之處:
v 當給定了Bezier曲線的控制點后,也就確定了曲線的次數。當次數過高時,會給Bezier曲線的計算帶來不便。如果采用分段三次Bezier曲線且要保持曲線間的連續性還必須有附加條件;
v Bezier曲線是整體定義的,改變任意一個控制點,將對整條曲線都有影響。因此Bezier不具有局部修改性。
1964年由Schoenberg提出了B樣條理論,1972年de Boor與Cox分別獨立給出了關于B樣條的標準算法。Gordon和Riesenfeld又把B樣條理論應用于形狀描述,最終提出了B樣條方法。用B樣條代替Bernstein基,構造出B樣條曲線,這種方法繼承了Bezier方法的一切優點,克服了Bezier方法的缺點,較成功地解決了局部控制問題,又輕而易舉地在參數連續性基礎上解決了連接問題,從而使自由曲線曲面形狀的描述問題得到較好解決。
B樣條方法具有表示與設計自由曲線曲面的強大功能,它不僅是最廣為流行的形狀數學描述的主流方法之一,而且已成為關于工業產品幾何定義國際標準的有理B樣條方法的基礎。從B樣條理論的發展歷程可以看出,理論與實踐的相互作用。正是由于實際的需要,才提出解決問題的新方法。
本文給出B樣條的遞推定義并使用OpenCascade的B樣條庫在OpenSceneGraph中繪制出B樣條基函數的曲線,在此基礎上來理解B樣條基函數的局部支撐性、節點向量的重復度等概念。
2. Definition of B-spline Basis Functions
有很多方法可以用來定義B樣條基函數以及證明它的一些重要性質。例如可以采用截尾冪函數的差商定義,開花定義及由de Boor和Cox等人提出的遞推公式等來定義。我們這里采用的是遞推定義方法,因為這種方法在計算機實現中是最有效的。
令U={u0,u1,…,um}是一個單調不減的實數序列,即ui<=ui+1,i=0,1,…,m-1。其中,ui稱為節點,U稱為節點矢量,用Ni,p(u)表示第i個p次B樣條基函數,其定義為:
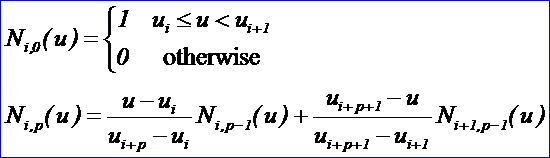
遞推公式的幾何意義可以歸結為:移位、升階和線性組合。由上述公式可知:
1) 當p>0時,Ni,p(u)是兩個p-1次基函數的線性組合;
2) 計算一組基函數時需要事先指定節點矢量U和次數p;
3) 計算p次基函數的過程生成一個如下形式的三角陣列:
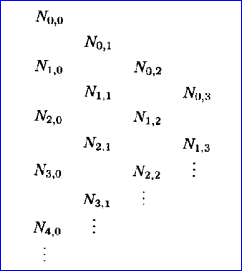
B樣條基有如下性質:
a) 遞推性;
b) 局部支承性;
c) 規范性;
d) 可微性;
關于B樣條基函數更多的定義方式,可以參考《計算幾何教程》、《自由曲線曲面造型技術》等。
3. Use OpenCascade B-spline Library
在OpenCascade中,B樣條的計算庫位于基礎模塊(FoundationClasses Module)的TKMath,有分別對曲線和曲面的底層計算類BSplCLib和BSplSLib。關于B樣條曲線計算庫中對B樣條基函數計算的實現方法見:B-Spline Curve Library in Open Cascade
http://m.shnenglu.com/eryar/archive/2013/03/12/198367.html 。
本文主要介紹將B樣條基函數的計算結果在OpenSceneGraph中顯示出來,以便于直觀的理解B樣條基的相關性質。程序代碼如下所示:
/*
* Copyright (c) 2014 eryar All Rights Reserved.
*
* File : Main.cpp
* Author : eryar@163.com
* Date : 2014-07-20 20:46
* Version : 1.0v
*
* Description : Show OpenCascade B-Spline Basis evaluate
* result in OpenSceneGraph.
*
* Key words : OpenCascade, OpenSceneGraph,
* B-Spline Basis Function
*/
// OpenSceneGraph library.
#include <osg/MatrixTransform>
#include <osgDB/ReadFile>
#include <osgViewer/Viewer>
#include <osgGA/StateSetManipulator>
#include <osgViewer/ViewerEventHandlers>
#pragma comment(lib, "osgd.lib")
#pragma comment(lib, "osgDBd.lib")
#pragma comment(lib, "osgGAd.lib")
#pragma comment(lib, "osgViewerd.lib")
// OpenCASCADE library.
#define WNT
#include <TColStd_Array1OfReal.hxx>
#include <math_Matrix.hxx>
#include <BSplCLib.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
osg::Node* BuildAxes(Standard_Real x, Standard_Real y)
{
osg::ref_ptr<osg::Geode> aGeode = new osg::Geode();
osg::ref_ptr<osg::Geometry> aLineGeom = new osg::Geometry();
osg::ref_ptr<osg::Vec3Array> aVertices = new osg::Vec3Array();
// x axis
aVertices->push_back(osg::Vec3(0.0, 0.0, 0.0));
aVertices->push_back(osg::Vec3(x + 0.5, 0.0, 0.0));
// arrow for x axis
aVertices->push_back(osg::Vec3(x + 0.5, 0.0, 0.0));
aVertices->push_back(osg::Vec3(x + 0.3, 0.0, 0.05));
aVertices->push_back(osg::Vec3(x + 0.5, 0.0, 0.0));
aVertices->push_back(osg::Vec3(x + 0.3, 0.0, -0.05));
// x ruler
for (Standard_Integer i = 1; i <= x; ++i)
{
aVertices->push_back(osg::Vec3(i, 0.0, 0.05));
aVertices->push_back(osg::Vec3(i, 0.0, -0.05));
}
// y axis
aVertices->push_back(osg::Vec3(0.0, 0.0, 0.0));
aVertices->push_back(osg::Vec3(0.0, 0.0, y + 0.5));
// arrow for y axis
aVertices->push_back(osg::Vec3(0.0, 0.0, y + 0.5));
aVertices->push_back(osg::Vec3(0.05, 0.0, y + 0.3));
aVertices->push_back(osg::Vec3(0.0, 0.0, y + 0.5));
aVertices->push_back(osg::Vec3(-0.05, 0.0, y + 0.3));
// y ruler
for (Standard_Integer j = 1; j <= y; ++j)
{
aVertices->push_back(osg::Vec3(0.05, 0.0, j));
aVertices->push_back(osg::Vec3(-0.05, 0.0, j));
}
aLineGeom->setVertexArray(aVertices);
aLineGeom->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINES, 0, aVertices->size()));
aGeode->addDrawable(aLineGeom);
return aGeode.release();
}
osg::Node* BuildBSplineBasis(const TColStd_Array1OfReal &theKnots, int theDegree)
{
osg::ref_ptr<osg::Group> aGroup = new osg::Group();
osg::ref_ptr<osg::Geode> aGeode = new osg::Geode();
osg::ref_ptr<osg::Geometry> aPointGeom = new osg::Geometry();
osg::ref_ptr<osg::Vec3Array> aVertices = new osg::Vec3Array();
Standard_Integer aIndex = 0;
Standard_Integer aOrder = theDegree + 1;
math_Matrix m(1, 1, 1, aOrder);
for (Standard_Real u = theKnots.Value(theKnots.Lower()); u <= theKnots.Value(theKnots.Upper()); u += 0.001)
{
BSplCLib::EvalBsplineBasis(0, 0, aOrder, theKnots, u, aIndex, m);
for (Standard_Integer i = 1; i <= aOrder; ++i)
{
aVertices->push_back(osg::Vec3(u, 0.0, m(1, i)));
}
}
aPointGeom->setVertexArray(aVertices);
aPointGeom->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::POINTS, 0, aVertices->size()));
// set the color for the points.
osg::ref_ptr<osg::Vec4Array> aColor = new osg::Vec4Array();
aColor->push_back(osg::Vec4(aOrder % 1, aOrder % 2, aOrder % 3, 1.0));
aPointGeom->setColorArray(aColor);
aPointGeom->setColorBinding(osg::Geometry::BIND_OVERALL);
aGeode->addDrawable(aPointGeom);
aGroup->addChild(aGeode);
aGroup->addChild(BuildAxes(theKnots.Value(theKnots.Upper()), 1.0));
return aGroup.release();
}
osg::Node* BuildBSplineBasis(void)
{
osg::ref_ptr<osg::Group> aGroupNode = new osg::Group();
TColStd_Array1OfReal aKnots1(1, 8);
aKnots1(1) = 0.0;
aKnots1(2) = 0.0;
aKnots1(3) = 0.0;
aKnots1(4) = 0.0;
aKnots1(5) = 1.0;
aKnots1(6) = 1.0;
aKnots1(7) = 1.0;
aKnots1(8) = 1.0;
osg::ref_ptr<osg::MatrixTransform> aUniformBasis = new osg::MatrixTransform();
aUniformBasis->setMatrix(osg::Matrix::translate(0.0, 0.0, 0.0));
aUniformBasis->addChild(BuildBSplineBasis(aKnots1, 4));
aGroupNode->addChild(aUniformBasis);
return aGroupNode.release();
}
int main(int argc, char* argv[])
{
osgViewer::Viewer aViewer;
aViewer.setSceneData(BuildBSplineBasis());
aViewer.addEventHandler(new osgGA::StateSetManipulator(aViewer.getCamera()->getOrCreateStateSet()));
aViewer.addEventHandler(new osgViewer::StatsHandler);
aViewer.addEventHandler(new osgViewer::WindowSizeHandler);
return aViewer.run();
}
B樣條基函數計算使用了函數BSplCLib::EvalBsplineBasis(),通過這個函數不僅可以計算基函數,還可以計算B樣條基函數的導數。計算結果輸出到一個矩陣之中。根據定義可知要計算B樣條基函數,需要指定節點矢量和次數,所以函數BuildBSplineBasis()就根據這兩個參數生成B樣條基函數的圖形進行顯示。上述代碼生成的一個B樣條基函數結果如下圖所示:
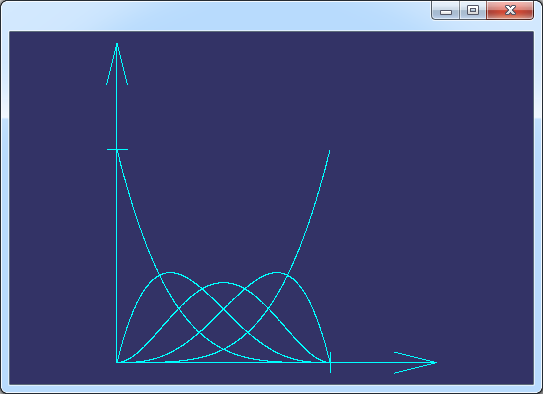
Figure 3.1 U=[0,0,0,0,1,1,1,1], p=4的B樣條基函數
改變次數,生成p=3時的基函數如下圖所示:
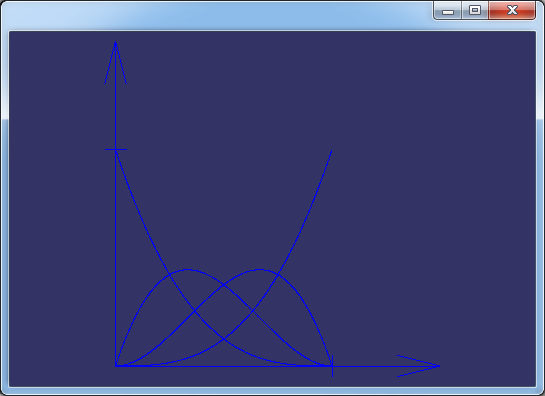
Figure 3.2 U=[0,0,0,0,1,1,1,1], p=3的B樣條基函數
4. Local Support Property
B樣條的局部支承性(Local Support Property)是B樣條最重要的性質之一,也是B樣條方法與Bezier方法的主要差別所在。由于局部支承性質,使B樣條曲線具有良好的局部性,從而為曲線、曲面設計奠定了良好的基礎。
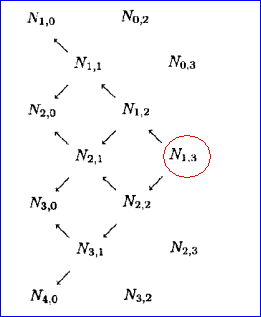
Figure 4.1 Local Support Property of B-spline Basis Function
從上圖可以看出,N1,3是N1,0,N2,0,N3,0,N4,0的線性組合,所以N1,3的非零區域只在u∈[u1, u5],即:
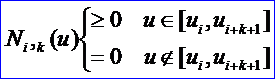
上式表明,第i條k次B樣條僅在節點ti到ti+k+1的k+1個區間內不為0,其他區間均為0.這個性質稱為局部支承性。
k次B樣條僅在k+1個區間內非0。換言之,每段k次B樣條曲線只涉及k+1個基函數,并由k+1個頂點所定義。B樣條的局部支承性對曲線、曲面設計有兩方面的影響:
v 第i段k次B樣條曲線僅由Pi, Pi+1, ..., Pi+k共k+1個頂點所控制,而與其他頂點無關。為此,為修改一段曲線,僅需修改有關的k+1個頂點即可;
v 反之,修改一個頂點,對B樣條曲線的影響也是局部的,對于均勻的k次B樣條曲線調整一個頂點的位置僅影響與該頂點有關的k+1段曲線。
局部支承性是B樣條方法最引人的特點之一。
5. Multiplicity of the Knot Vector
重節點連續階性質:在每一個節點區間(ui, ui+1)內部,Ni,p(u)為多項式,因此有導數存在。在一個節點ui處,Ni,p(u)是一個p-mi次連續可微的,此處mi是該節點的重數(Multiplicity)。所以增加次數,則增加連續性,而增加節點的重數,則降低連續性。
節點矢量U={0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5}上的2次B樣條基函數如下圖所示:
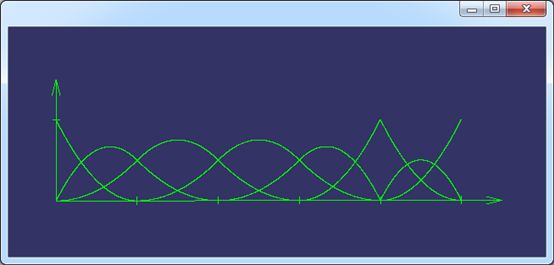
Figure 5.1 U={0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5} p = 2 B-spline Basis Function
程序代碼如下所示:
TColStd_Array1OfReal aKnots2(1, 11);
aKnots2(1) = 0.0;
aKnots2(2) = 0.0;
aKnots2(3) = 0.0;
aKnots2(4) = 1.0;
aKnots2(5) = 2.0;
aKnots2(6) = 3.0;
aKnots2(7) = 4.0;
aKnots2(8) = 4.0;
aKnots2(9) = 5.0;
aKnots2(10) = 5.0;
aKnots2(11) = 5.0;
osg::ref_ptr<osg::MatrixTransform> aNonUniformBasis2 = new osg::MatrixTransform();
aNonUniformBasis2->addChild(BuildBSplineBasis(aKnots2, 2));
aGroupNode->addChild(aNonUniformBasis2);
從上圖可知,在節點u=4的位置,B樣條基函數的曲線已經失去了連續性。再舉一個例子,節點矢量U={0,0,0,0,1,2,3,4,4,4,5,5,5,5},p=3的B樣條基函數如下圖所示:

Figure 5.2 U={0, 0, 0, 0,1, 2, 3, 4, 4,4, 5, 5, 5,5} p = 3 B-spline Basis Function
當節點矢量兩端的重復度如下所示時,則B樣條基函數退化為Bernstein基函數:

因此,Bezier可以看作是B樣條表達式的一種特例。在OpenCascade的B樣條計算類中有一個函數可以根據次數p來生成Bezier的節點矢量:
//=====================================================================
// function: FlatBezierKnots
// purpose :
//=====================================================================
// array of flat knots for bezier curve of maximum 25 degree
static const Standard_Real knots[52] = { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };
const Standard_Real& BSplCLib::FlatBezierKnots (const Standard_Integer Degree)
{
Standard_OutOfRange_Raise_if (Degree < 1 || Degree > MaxDegree() || MaxDegree() != 25,
"Bezier curve degree greater than maximal supported");
return knots[25-Degree];
}
由上述代碼可知,函數FlatBezierKnots()直接返回了靜態數組變量knots中的部分值,且Bezier的次數最高不能超過25次。
6. Conclusion
B樣條基函數是NURBS理論的基礎,本文結合OpenCascade中的B樣條計算庫,將其計算結果在OpenSceneGraph中顯示出來,以便直觀的理解B樣條的有關性質,如局部支承性、節點重復度等概念。
讀者可以結合上述代碼,嘗試給出不同的節點矢量及次數,來觀察B樣條基函數的結果,直觀的理解B樣條的性質,進而結合源程序來理解B樣條基函數的具體實現。
7. References
1. 趙罡,穆國旺,王拉柱譯Les Piegl,Wayne Tiller The NURBS Book(Second Edition) 2010 清華大學出版社
2. 莫容,常智勇 計算機輔助幾何造型技術 2009 科學出版社
3. 朱心雄等,自由曲線曲面造型技術,2000,科學出版社
4. Kelly Dempski, Focus on Curves and Surface, 2003, Premier Press
5. 王仁宏,李崇君,朱春鋼 計算幾何教程 2008 科學出版社