OpenCascade Eigenvalues and Eigenvectors of Square Matrix
eryar@163.com
Abstract. OpenCascade use the Jacobi method to find the eigenvalues and the eigenvectors of a real symmetric square matrix. Use class math_Jacobi to computes all eigenvalues and eigenvectors by using Jacobi method. The exception NotSquare is raised if the matrix is not square. No verification that the matrix is really symmetric is done.
Key words. Eigenvalues, Eigenvectors, OpenCascade, Matrix, Jacobi method,
1. Introduction
工程技術(shù)中的一些問題,如振動(dòng)問題和穩(wěn)定性問題��,?��?蓺w結(jié)為求一個(gè)方陣的特征值和特征向量的問題�����。數(shù)學(xué)中諸如方陣的對(duì)角化及解常微分方程等問題,也都有要用到特征值的理論。
定義:設(shè)A是n階矩陣,如果數(shù)λ和n維非零列向量x使關(guān)系式 Ax = λx成立,那么這樣的數(shù)λ稱為方陣A的特征值�����,非零向量x稱為A對(duì)應(yīng)于特征值λ的特征向量���。
推論:若n階矩陣A與對(duì)角陣

相似���,則λ1,λ2,...,λn即是A的n個(gè)特征值���。
定理:n階矩陣A與對(duì)角陣相似(即A能對(duì)角化)的充分必要條件是A有n個(gè)線性無關(guān)的特征向量��。
推論:如果n階矩陣A的n個(gè)特征值互不相等�����,則A與對(duì)角陣相似。
當(dāng)A的特征方程有重根時(shí),就不一定有n個(gè)線性無關(guān)的的特征向量��,從而不一定能對(duì)角化��。一個(gè)n階矩陣具備什么條件才能對(duì)角化呢���?這是一個(gè)較復(fù)雜的問題�����。
定理:設(shè)A為n階對(duì)稱陣���,則有正交陣P��,使
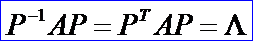
其中∧是以A的n個(gè)特征值為對(duì)角元的對(duì)角陣�����。
OpenCascacde中使用了Jacobi方法來計(jì)算對(duì)稱方陣的特征值和特征向量��。本文對(duì)math_Jacobi的使用進(jìn)行詳細(xì)說明。
2. Code Example
結(jié)合同濟(jì)第四版《線性代數(shù)》中的例子��,來驗(yàn)證Jacobi方法計(jì)算的結(jié)果���。示例程序如下所示:
/*
* Copyright (c) 2014 eryar All Rights Reserved.
*
* File : Main.cpp
* Author : eryar@163.com
* Date : 2014-06-22 21:46
* Version : 1.0v
*
* Description : Demonstrate how to find the eigenvalues and
* eigenvectors for a symmetric square Matrix.
* 題目來自《線性代數(shù)》同濟(jì) 第四版
*
*/
#define WNT
#include <math_Jacobi.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
/**
* OpenCascade use Jacobi method to find the eigenvalues and
* the eigenvectors of a real symmetric square matrix.
*/
void EvalEigenvalue(const math_Matrix &A)
{
math_Jacobi J(A);
std::cout << A << std::endl;
if (J.IsDone())
{
std::cout << "Jacobi: \n" << J << std::endl;
//std::cout << "Eigenvalues: \n" << J.Values() << std::endl;
//std::cout << "Eigenvectors: \n" << J.Vectors() << std::endl;
for (Standard_Integer i = A.LowerRow(); i <= A.UpperRow(); ++i)
{
math_Vector V(1, A.RowNumber());
J.Vector(i, V);
std::cout << "Eigenvalue: " << J.Value(i) << std::endl;
std::cout << "Eigenvector: " << V << std::endl;
}
}
}
void TestJacobi(void)
{
// 1. P120 Example 5:
math_Matrix A1(1, 2, 1, 2, 0.0);
A1(1, 1) = 3.0; A1(1, 2) = -1.0;
A1(2, 1) = -1.0; A1(2, 2) = 3.0;
EvalEigenvalue(A1);
// 2. P120 Example 6:
math_Matrix A2(1, 3, 1, 3, 0.0);
A2(1, 1) = -1.0; A2(1, 2) = 1.0; A2(1, 3) = 0.0;
A2(2, 1) = -4.0; A2(2, 2) = 3.0; A2(2, 3) = 0.0;
A2(3, 1) = 1.0; A2(3, 2) = 0.0; A2(3, 3) = 2.0;
EvalEigenvalue(A2);
// 3. P120 Example 7:
math_Matrix A3(1, 3, 1, 3, 0.0);
A3(1, 1) = -2.0; A3(1, 2) = 1.0; A3(1, 3) = 1.0;
A3(2, 1) = 0.0; A3(2, 2) = 2.0; A3(2, 3) = 0.0;
A3(3, 1) = -4.0; A3(3, 2) = 1.0; A3(3, 3) = 3.0;
EvalEigenvalue(A3);
// 4. P127 Example 12:
math_Matrix A4(1, 3, 1, 3, 0.0);
A4(1, 1) = 0.0; A4(1, 2) = -1.0; A4(1, 3) = 1.0;
A4(2, 1) = -1.0; A4(2, 2) = 0.0; A4(2, 3) = 1.0;
A4(3, 1) = 1.0; A4(3, 2) = 1.0; A4(3, 3) = 0.0;
EvalEigenvalue(A4);
// 5. P138 Execise 5(3);
math_Matrix A5(1, 3, 1, 3, 0.0);
A5(1, 1) = 1.0; A5(1, 2) = 2.0; A5(1, 3) = 3.0;
A5(2, 1) = 2.0; A5(2, 2) = 1.0; A5(2, 3) = 3.0;
A5(3, 1) = 3.0; A5(3, 2) = 3.0; A5(3, 3) = 6.0;
EvalEigenvalue(A5);
}
int main(int argc, char* argv[])
{
// The Jacobi method to find the eigenvalues and
// eigenvectors of a real symmetric square matrx.
// The exception NotSquare is raised if the matrix is not square.
// No verification that the matrix is really symmetric is done.
TestJacobi();
return 0;
}
計(jì)算結(jié)果部分如下圖所示:
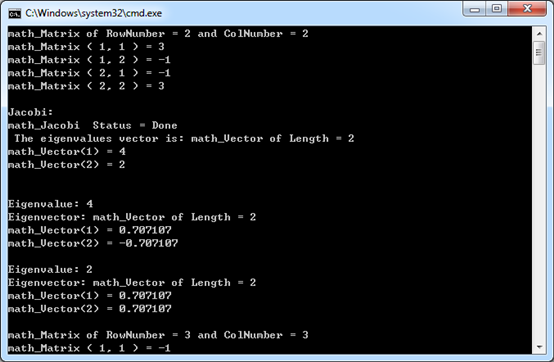
Figure 2.1 Jacobi method Result
3. Conclusion
矩陣的特征值和特征向量的理論能用來求解微分方程組的問題�����。振動(dòng)分析���、現(xiàn)代控制理論中的數(shù)學(xué)模型都可歸結(jié)為對(duì)微分方程組的求解���。因此���,對(duì)特征值和特征向量的數(shù)值計(jì)算有重要的意義�����。
OpenCascade中提供了使用Jacobi方法來計(jì)算特征值和特征向量的類math_Jacobi。從計(jì)算結(jié)果可以看出��,math_Jacobi只對(duì)對(duì)稱方陣的計(jì)算結(jié)果準(zhǔn)確�����,若不是對(duì)稱陣,則計(jì)算結(jié)果是不準(zhǔn)確的���。
會(huì)使用OpenCascade中現(xiàn)成的算法是一回事,能實(shí)現(xiàn)這些算法又是另外一回事�����。對(duì)計(jì)算特征值和特征向量的數(shù)值方法感興趣的讀者�����,可以參考《計(jì)算方法》或《數(shù)值分析》等相關(guān)書籍�����。
4. References
1. 同濟(jì)大學(xué)應(yīng)用數(shù)學(xué)系. 線性代數(shù). 高等教育出版社. 2003
2. 易大義, 沈云寶, 李有法. 計(jì)算方法. 浙江大學(xué)出版社. 2002
3. 楊明, 李先忠. 矩陣論. 華中科技大學(xué)出版社. 2005