Parametric Curves and Surfaces

eryar@163.com

Abstract. This paper is concerned with parametric curves and surfaces definitions, such as singular point and regular point and their application in OpenCascade. The two most common methods of representing curves and surfaces in geometric modeling are implicit equations and parametric functions. Successful geometric modeling is done using both techniques. When you use parametric functions to represent curves and surfaces, you need to pay attention for the characteristic of it, such as singularity of parametric functions.

Key words. OpenCascade, Parametric Curves, Parametric Surfaces, Singular Point, Regular Point

1. Introduction

在幾何造型中，兩種最常用的曲線曲面表示方法是隱式表示（Implicit equations）和參數(shù)表示（Parametric functions）。其中參數(shù)表示由于構(gòu)造簡單、計算容易、數(shù)值穩(wěn)定等特點而流行于世并成為幾何造型的主要方法之一。相比于參數(shù)曲線曲面，隱式表示法同樣具有自身的優(yōu)勢，如判定點是否位于曲面上很方便。在幾何造型內(nèi)核OpenCascade中，主要也是采用參數(shù)表示法來表示曲線曲面，因為有理、非有理B樣條曲線曲面及Bezier曲線曲面都是參數(shù)表示的。本文主要結(jié)合OpenCascade對參數(shù)表示的曲線曲面一些性質(zhì)進行說明，如因參數(shù)化引起的奇異性的處理等，學(xué)習(xí)如何將數(shù)學(xué)定義應(yīng)用到實際程序中的思想。

2. Preliminaries

2.1 Parametric Curves

根據(jù)向量函數(shù)的概念，空間中一條曲線可以表示為參數(shù)t的向量函數(shù)，

曲線的這種表示方法稱為曲線的參數(shù)表示，[a, b]稱之為參數(shù)域。給定了一個具體的曲線方程，稱之為給定了一個曲線的參數(shù)化。顯然，同一條曲線的參數(shù)化可能是不同的。如果，

稱為曲線p(t)在t=t0是正則的，則p(t0)稱為曲線的正則點（Regular Point）。由上式，點p(t0)為正則點的充要條件為x(t0), y(t0), z(t0)的導(dǎo)數(shù)不同時為零。若曲線p(t)的所有點都是正則點，就稱曲線p(t)為正則曲線。非正則的點稱為奇點（Singular Point）。值得注意的是，同一條曲線上的一個點，在某些參數(shù)化下為正則點，但是在另外的參數(shù)化下可能不是正則點。

例如直線：

為正則曲線，沒有奇點。而直線：

表示為同一直線，但是它在以下情況下有兩個奇點：

如果曲線p(t)的所有分量函數(shù)x(t), y(t), z(t)的k階導(dǎo)數(shù)存在且連續(xù)，并且曲線p(t)是正則曲線，則稱曲線屬于Ck類的。

2.2 Parametric Surfaces

用兩個變量u, v的向量函數(shù)p(u,v)描述的曲面稱為曲面的參數(shù)表示。

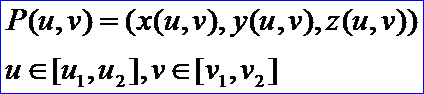
參數(shù)u,v通常的變化區(qū)間為uv平面上的一個矩形區(qū)域。如果圖2.2.1所示為從參數(shù)空間到三維實向量空間（即模型空間）的映射。給定了曲面的參數(shù)方程就給定了曲面的一個參數(shù)化，也決定了參數(shù)域[u1, u2]和[v1, v2]上的點與曲面上點的對應(yīng)關(guān)系。顯然曲面的參數(shù)化也不是唯一的。

Figure 2.2.1 Parametric Surface

如果固定一個參數(shù)，例如v=v0，那么p(u, v0)為單參數(shù)u的向量函數(shù)，它表示曲面上的一條曲線，稱為等參線（Isoparametric curve）或u曲線（u constant Isoparametric curve）。顯然曲面p(u, v)上存在兩簇等參線即一簇u線和一簇v線。如圖2.2.2所示：

Figure 2.2.2 Parametric surface and Isoparametric curves

曲面上的點p(u0,v0)沿u和v線方向的切向量分別為：

如果切向量pu(u0,v0)和pv(u0,v0)不平行，即：

則稱點p(u0,v0)為曲面的正則點（Regular Point），否則稱為奇點（Singular Point）。如果曲面p(u,v)上所有點都是正則點，即曲面上每點都存在法向量，就稱這樣的參數(shù)化曲面為正則的。

Figure 2.2.3 Tangents on a surface

曲面上過任意點p的切向量為上述兩個偏導(dǎo)數(shù)的線性組合，因此其切線位于這兩個向量所張成的平面內(nèi)，如圖2.2.3所示。這個平面稱為曲面在點p的切平面。稱過點p且垂直于該點切平面的直線為法線，與兩個切向量滿足右手法則，法向量為這兩個向量的叉乘：

曲面上任意點處的法向量如圖2.2.4所示：

Figure 2.2.4 Normal on a surface

3. Advantages of Parametric Functions

3.1 有界性 Bounded

參數(shù)表示法易于規(guī)定曲線曲面的范圍。在參數(shù)表示形式中，曲線曲面的有界性由參數(shù)區(qū)間的有界性自然得到。另一方面，無界的幾何元素如直線，利用參數(shù)方法表示也是不方便的。OpenCascade的拓樸結(jié)構(gòu)中TopoDS_Edge和TopoDS_Face包含的幾何元素都是有界的，主要是因為其中的幾何曲線曲面是參數(shù)表示的。

Figure 3.1 Get bound of parametric curve and surface

3.2 有向性 Orientation

曲線的參數(shù)表示同時給出了曲線的一個方向（natural direction），如設(shè)a≤u≤b，曲線C(u)方向為從C(a)到C(b)。對于曲面而言，方向為曲面的法向。

在OpenCascade中使用枚舉TopAbs_Orientation定義了方向的幾中類型。若拓樸邊的朝向為TopAbs_FORWARD，則表示邊的的邏輯方向與參數(shù)曲線的natural direction相同；若為TopAbs_REVERSED，則表示邏輯方向與參數(shù)曲線的natural direction相反。類似地，若拓樸面的朝向為TopAbs_FORWARD，則面的朝向與參數(shù)曲面的法向相同；若面的朝向為TopAbs_REVERSED，則面的朝向與參數(shù)曲面的法向相反。

Figure 3.2 Orientation of TopoDS_Shape

3.3 易于計算 Easy to Evaluate Value

參數(shù)曲線曲面上點的計算很簡單，只需要根據(jù)參數(shù)直接可計算出曲線曲面上的點。計算曲線曲面上點的切向量等也很方便。

Figure 3.3 Get point on parametric curve and surface

3.4 易于分段描述 Piecewise Curves and Surfaces

3.5 直觀自然 Natural for Designing and Representing Shape

在用計算機進行形狀設(shè)計和表示時，參數(shù)形式更直觀、自然。在很多參數(shù)表示形式中，如Bezier和B樣條系統(tǒng)具有相當(dāng)重要的幾何意義。這導(dǎo)致直觀的設(shè)計方法和具有幾何特色、數(shù)值穩(wěn)定的算法。

4. Disadvantages of Parametric Functions

任何事物都不是完美的，既存在有利的一面，也存在不利的一面，參數(shù)表示法也不例外。因此也有人對參數(shù)表示與隱式表示之間的轉(zhuǎn)換進行了研究，以便在適當(dāng)?shù)那闆r下選擇更適合的計算方式。

4.1 判斷點是否在曲線曲面上 Determine if a point is on the curve or surface

當(dāng)計算曲線曲面上的點時，采用隱式表示形式是困難的，用參數(shù)表示就很容易；但當(dāng)給定一個點，要判斷它是否在曲線或曲面上時，采用參數(shù)形式很困難，但是使用隱式給示就很容易。

盡管用參數(shù)表示不易判斷點是否在曲線曲面上，在OpenCascade中也只能在一定的偏差范圍Tolerance內(nèi)來判定點是否在參數(shù)曲線曲面上。類GeomLib_Tool提供了相關(guān)的功能：

Figure 4.1 Compute the parameters of a given point for curve and surface

4.2 處理參數(shù)化引起的奇異性 Deal with parametric anomalies

當(dāng)采用參數(shù)形式時，經(jīng)常需要處理由參數(shù)化引起的奇異性（Singularity），而這種奇異性并不是由于本身的幾何特性引起的。典型的例子是用參數(shù)表示的球面。按參數(shù)方程它的兩個極點是奇點，處理時需要特別注意。但在幾何上，兩個極點和球面上的其他點并無不同之處。下面結(jié)合OpenCascade中球面的參數(shù)方程進行說明。

在OpenCascade中球面的參數(shù)方程為：

分別沿u,v方向求偏導(dǎo)矢，即分別沿經(jīng)線和緯線的速度矢量，得：

曲面在一點處存在法矢及相應(yīng)切平面是曲面的幾何性質(zhì)，與曲面的參數(shù)化無關(guān)。因此，盡管不同的參數(shù)化會產(chǎn)生不同的偏導(dǎo)矢，但只要u或v方向上的切矢都不為零，則將u,v的切矢叉乘單位化后的法向是都是相同的。OpenCascade中的球面，對于所有的u∈[0, 2π]有：

即Su在球面的北極和南極消失（為零矢量），對應(yīng)v=-π/2和v=π/2時的兩個邊就分別退化（Degenerated）成兩個點。很明顯，球面在兩個極點的法矢確實是存在的，但在這種參數(shù)化之下，無法用上述方法來計算它的法向量。

Figure 4.2 Singularity of Sphere and its Degenerated Edges

OpenCascade中還有銜接邊（Seam Edge）的概念。參數(shù)區(qū)域的矩形范圍內(nèi)的兩個對邊可以映射成模型空間中的同一條邊，這樣的邊就稱為銜接邊（Seam Edge）。矩形區(qū)域也可映射成模型空間中的一個點，根據(jù)正則點和奇點的定義可知，這樣的點為奇點（Singular Point），對應(yīng)的邊為退化邊（Degenerated Edge）。

Figure 4.3 Singularity of Cone and its Seam Edge

由曲線曲面的正則與奇異性定義來理解OpenCascade中Degenerated的意義。

下面通過程序來驗證OpenCascade中參數(shù)表示的球面的兩個退化邊的參數(shù)對應(yīng)為v=-π/2和v=π/2。

5. Code Demo

通過程序示例來說明OpenCascade中參數(shù)表示的球面具有奇異性的兩個退化邊對應(yīng)的參數(shù)為v=-π/2和v=π/2。程序還演示了如何從拓樸子結(jié)構(gòu)找到與其相關(guān)的父結(jié)構(gòu)，如通過拓樸邊找到與其相關(guān)的面。

程序輸出結(jié)果如下所示：

由上輸出結(jié)果可知，當(dāng)球上的邊為退化邊時，對應(yīng)的參數(shù)u∈[0, 2π]，v=-π/2和v=π/2。

6. Conclusions

本文通過參數(shù)曲線曲面的相關(guān)定義，來理解曲線曲面參數(shù)表示法的特性。通過正則點、奇點的定義來理解參數(shù)表示法中存在的奇異現(xiàn)象。結(jié)合OpenCascade中球面的參數(shù)方程，分析其奇異性，進而去理解OpenCascade中因奇異性導(dǎo)致的退化（Degenerated）現(xiàn)象的處理。關(guān)于曲線曲面參數(shù)表示的奇異性的更多內(nèi)容可以參考相關(guān)書籍。

7. Acknowledgments

感謝OpenCascade Team努力的工作與開放的態(tài)度，才有機會接觸到并從中學(xué)到幾何造型相關(guān)知識。

感謝OpenSceneGraph對OpenGL的包裝，使OpenGL的使用更方便。

感謝全世界志趣相投的朋友們的鼓勵與支持，與你們的討論交流使我受益匪淺，并樂在其中。

感謝WPS提供了免費版本的文檔編輯工具，方便了文檔的編輯及導(dǎo)出為PDF文件。

我想引用大學(xué)英語課本中第一課中的話來描述一下此時的感受：

Learning a foreign language was one of the most difficult yet most rewarding experiences of my life. Although at times, learning a language was frustrating it was well worth the effort.

Learning a foreign language has been a most trying experience for me, but one that I wouldn’t trade for anything. Not only did learning another language teach me the value of hard work, but it also gave me insights into another culture, and my mind was opened to new ways of seeing things. The most wonderful result of having learned a foreign language was that I could communicate with many more people than before. Talking with people is one of my favorite activities, so being able to speak a new language lets me meet new people, participate in conversations, and form new, unforgettable friendships. Now that I speak a foreign language, instead of staring into space when English is being spoken, I can participate and make friends. I am able to reach out to others and bridge the gap between my language and culture and theirs.

把其中的a foreign language換成OpenCascade或其他新鮮事物也同樣適用。

8. References

1. Les Piegl, Wayne Tiller, The NURBS Book, Springer-Verlag, 1997

2. 王仁宏, 李崇君, 朱春鋼. 計算幾何教程. 科學(xué)出版社, 2008

3. Roman Lygin. OpenCASCADE Notes. http://opencascade.blogspot.com