OpenCascade Matrix
eryar@163.com
摘要Abstract:本文對(duì)矩陣作簡要介紹,并結(jié)合代碼說明OpenCascade矩陣計(jì)算類的使用方法。
關(guān)鍵字Key Words:OpenCascade、Matrix、C++
一、引言Introduction
矩陣的研究歷史悠久,拉丁方陣和幻方在史前年代已有人研究。作為解決線性方程的工具,矩陣也有不短的歷史。1693年,微積分的發(fā)現(xiàn)者之一萊布尼茨建立了行列式論(theory of determinants)。1750年,克拉默又定下了克拉默法則。1800年代,高斯和威廉若爾當(dāng)建立了高斯-若爾當(dāng)消去法。
從其發(fā)展歷史可以看出,從行列式論的提出到克拉默法則總共歷時(shí)50多年之久,而在我們《線性代數(shù)》的課本中,也就是一章的內(nèi)容,學(xué)習(xí)時(shí)間可能只有一個(gè)星期。難怪這些概念這么抽象晦澀,也是情有可原的,哈哈。不過,當(dāng)理解這些概念,也就掌握了一個(gè)強(qiáng)大的工具,因?yàn)樗彩褂行┯?jì)算統(tǒng)一、簡單。
矩陣是高等代數(shù)中的常見工具,也常見于統(tǒng)計(jì)分析等應(yīng)用數(shù)學(xué)學(xué)科中。在物理學(xué)中,矩陣用于電路學(xué)、力學(xué)、光學(xué)和量子物理中都有應(yīng)用;計(jì)算機(jī)科學(xué)中,三維變換就是使用了矩陣的線性變換。矩陣的運(yùn)算是數(shù)值分析領(lǐng)域的重要問題。
在計(jì)算機(jī)圖形相關(guān)的軟件中,矩陣是必不可少的重要工具。如:OpenGL、DirectX中的變換都是用矩陣實(shí)現(xiàn)的;OpenCascade中就有矩陣計(jì)算類(math_Matrix);OpenSceneGraph中也有矩陣的計(jì)算類(osg::Matrix)等等。矩陣在計(jì)算中主要用來表達(dá)線性變換,統(tǒng)一三維空間中物體的位置和方向變換。
本文主要介紹OpenCascade中矩陣類的使用方法。
二、矩陣的運(yùn)算 Matrix Calculation
矩陣的運(yùn)算主要有矩陣的加法、數(shù)與矩陣相乘、矩陣與矩陣相乘、矩陣的轉(zhuǎn)置、方陣的行列式、共軛矩陣、逆矩陣。還有通過矩陣來求解線性方程組的解問題。
1. 矩陣的加法 Matrix Addition
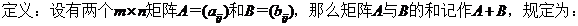
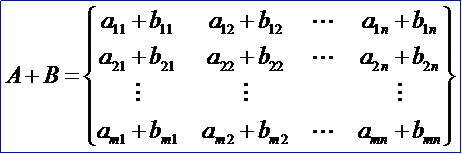
應(yīng)該注意,只有當(dāng)兩個(gè)矩陣是同型矩陣時(shí),才能進(jìn)行加法運(yùn)算。矩陣加法滿足下列運(yùn)算規(guī)律:設(shè)A、B、C都是m×n矩陣:

2. 數(shù)與矩陣相乘 Matrix Multiplication


數(shù)乘矩陣滿足下列運(yùn)算規(guī)律(設(shè)A、B為m×n矩陣,λ、μ為數(shù)):
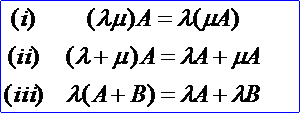
矩陣相加與矩陣相乘合起來,統(tǒng)稱為矩陣的線性運(yùn)算。
3. 矩陣與矩陣相乘 Matrix Multiplication
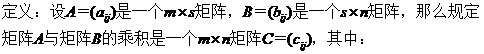

并把此乘積記作:C = AB
按此定義,一個(gè)1×s行矩陣與一個(gè)s×1列矩陣的乘積是一個(gè)1階方陣,也就是一個(gè)數(shù):
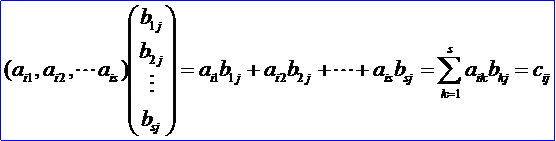
由此表明乘積矩陣AB=C的(i,j)元cij就是A的第i行與B的第j列的乘積。必須注意:只有當(dāng)每一個(gè)矩陣(左矩陣)的列數(shù)等于第二個(gè)矩陣(右矩陣)的行數(shù)時(shí),兩個(gè)矩陣才能相乘。
矩陣的乘法雖不滿足交換律,但仍滿足下列結(jié)合律和分配律(假設(shè)運(yùn)算都是可行的):
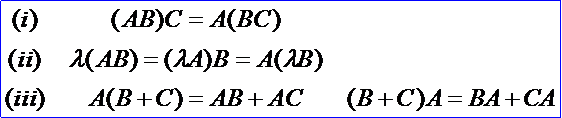
4. 矩陣的轉(zhuǎn)置 Matrix Transpose
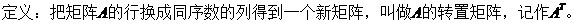
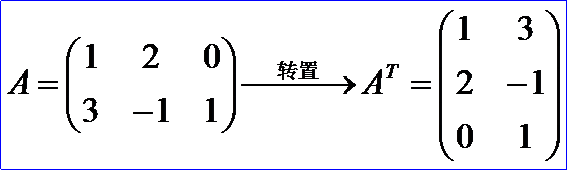
矩陣轉(zhuǎn)置也是一種運(yùn)算,滿足下列運(yùn)算規(guī)律(假設(shè)運(yùn)算都是可行的):
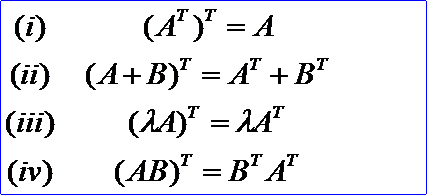
5. 方陣的行列式 Determinant of the Square Matrix

應(yīng)該注意,方陣與行列式是兩個(gè)不同的概念,n階方陣是n×n個(gè)數(shù)按一定方式排列成的數(shù)表,而n階行列式是這些數(shù)(也就是數(shù)表A)按一定的運(yùn)算法則所確定的一個(gè)數(shù)。
由A確定|A|的這個(gè)運(yùn)算滿足下述運(yùn)算規(guī)律(設(shè)A、B為n階方陣,λ為數(shù)):

6. 逆矩陣 Inverse of Matrix
定義:對(duì)于n階矩陣A,如果一個(gè)n階矩陣B,使AB=BA=E,則說矩陣A是可逆的,并把矩陣B稱為A的逆矩陣,簡稱逆陣。
方陣的逆矩陣滿足下列運(yùn)算規(guī)律:

7. 線性方程組的數(shù)值解法
在自然科學(xué)和工程中有很多問題的解決都?xì)w結(jié)為求解線性方程組或者非線性方程組的數(shù)學(xué)問題。例如,電學(xué)中的網(wǎng)絡(luò)問題,用最小二乘法求實(shí)驗(yàn)數(shù)據(jù)的網(wǎng)線擬合問題,三次樣條的插值問題,用有限元素法計(jì)算結(jié)構(gòu)力學(xué)中的一些問題或用差分法解橢圓型偏微分方程的邊值問題等等。
求解線性方程組的直接法主要有選主元高斯消去法、平方根法、追趕法等。如果計(jì)算過程中沒有舍入誤差,則此種方法經(jīng)過有限步算術(shù)運(yùn)算可求得方程組的精確解,但實(shí)際計(jì)算中由于舍入誤差的存在和影響,這種方法也只能求得方程組的近似解。目前這種方法是計(jì)算機(jī)上解低階稠密矩陣的有效方法。
高斯消去法是一個(gè)古老的求解線性方程組的方法,但由于它改進(jìn)得到的選主元的高斯消去法則是目前計(jì)算機(jī)上常用的解低階稠密矩陣方程組的有效方法。
用高斯消去法解方程組的基本思想是用矩陣行的初等變換將系數(shù)矩陣化為具有簡單形式的矩陣,即三角形矩陣,再通過回代過程,求出方程組的解。
三、OpenCascade矩陣計(jì)算
在OpenCascade中,矩陣的計(jì)算類是math_Matrix,它可以有任意的行數(shù)和列數(shù),實(shí)現(xiàn)了矩陣大部分的運(yùn)算。以下通過程序?qū)嵗齺碚f明math_Matrix的使用方法:
/*
* Copyright (c) 2013 eryar All Rights Reserved.
*
* File : Main.cpp
* Author : eryar@163.com
* Date : 2013-07-17 21:46
* Version : 1.0v
*
* Description : Demonstrate how to use math_Matrix class.
* 題目來自《線性代數(shù)》同濟(jì) 第四版
*
*/
#include <math_Matrix.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
int main(int argc, char* argv[])
{
math_Matrix A(1, 3, 1, 3);
math_Matrix B(1, 3, 1, 3);
math_Matrix C(1, 3, 1, 3);
// 1. Test Matrix Transpose and multiply.
// 題目來自P53習(xí)題二 第3題
// Set value of Matrix A
A.Init(1);
A(2, 3) = -1;
A(3, 2) = -1;
// Set value of Matrix B
B(1, 1) = 1; B(1, 2) = 2; B(1, 3) = 3;
B(2, 1) = -1; B(2, 2) = -2; B(2, 3) = 4;
B(3, 1) = 0; B(3, 2) = 5; B(3, 3) = 1;
C.TMultiply(A, B);
cout<<"Matrix A: "<<endl;
cout<<A<<endl;
cout<<"Matrix B: "<<endl;
cout<<B<<endl;
cout<<"Matrix C: "<<endl;
cout<<C<<endl;
// 2. Test the Determinant of the Matrix.
// 題目來自P12 例7
math_Matrix D(1, 4, 1, 4);
D(1, 1) = 3; D(1, 2) = 1; D(1, 3) = -1; D(1, 4) = 2;
D(2, 1) = -5; D(2, 2) = 1; D(2, 3) = 3; D(2, 4) = -4;
D(3, 1) = 2; D(3, 2) = 0; D(3, 3) = 1; D(3, 4) = -1;
D(4, 1) = 1; D(4, 2) = -5; D(4, 3) = 3; D(4, 4) = -3;
cout<<"Matrix D: "<<endl;
cout<<D<<endl;
cout<<"Determinant of Matrix D: "<<D.Determinant()<<endl;
// 3. Calculate Inverse of the Matrix.
// 題目來自P54 11題(3) 和P56 30題(1)
math_Matrix E(1, 3, 1, 3);
E(1, 1) = 1; E(1, 2) = 2; E(1, 3) = -1;
E(2, 1) = 3; E(2, 2) = 4; E(2, 3) = -2;
E(3, 1) = 5; E(3, 2) = -4; E(3, 3) = 1;
cout<<"Inverse of the Matrix E: "<<endl;
cout<<E.Inverse()<<endl;
// P56 30題(1)
math_Matrix F(1, 4, 1, 4);
F(1, 1) = 5; F(1, 2) = 2;
F(2, 1) = 2; F(2, 2) = 1;
F(3, 3) = 8; F(3, 4) = 3;
F(4, 3) = 5; F(4, 4) = 2;
cout<<"Inverse of the Matrix F: "<<endl;
cout<<F.Inverse()<<endl;
return 0;
}
計(jì)算結(jié)果為:
1 Matrix A:
2 math_Matrix of RowNumber = 3 and ColNumber = 3
3 math_Matrix ( 1, 1 ) = 1
4 math_Matrix ( 1, 2 ) = 1
5 math_Matrix ( 1, 3 ) = 1
6 math_Matrix ( 2, 1 ) = 1
7 math_Matrix ( 2, 2 ) = 1
8 math_Matrix ( 2, 3 ) = -1
9 math_Matrix ( 3, 1 ) = 1
10 math_Matrix ( 3, 2 ) = -1
11 math_Matrix ( 3, 3 ) = 1
12
13 Matrix B:
14 math_Matrix of RowNumber = 3 and ColNumber = 3
15 math_Matrix ( 1, 1 ) = 1
16 math_Matrix ( 1, 2 ) = 2
17 math_Matrix ( 1, 3 ) = 3
18 math_Matrix ( 2, 1 ) = -1
19 math_Matrix ( 2, 2 ) = -2
20 math_Matrix ( 2, 3 ) = 4
21 math_Matrix ( 3, 1 ) = 0
22 math_Matrix ( 3, 2 ) = 5
23 math_Matrix ( 3, 3 ) = 1
24
25 Matrix C:
26 math_Matrix of RowNumber = 3 and ColNumber = 3
27 math_Matrix ( 1, 1 ) = 0
28 math_Matrix ( 1, 2 ) = 5
29 math_Matrix ( 1, 3 ) = 8
30 math_Matrix ( 2, 1 ) = 0
31 math_Matrix ( 2, 2 ) = -5
32 math_Matrix ( 2, 3 ) = 6
33 math_Matrix ( 3, 1 ) = 2
34 math_Matrix ( 3, 2 ) = 9
35 math_Matrix ( 3, 3 ) = 0
36
37 Matrix D:
38 math_Matrix of RowNumber = 4 and ColNumber = 4
39 math_Matrix ( 1, 1 ) = 3
40 math_Matrix ( 1, 2 ) = 1
41 math_Matrix ( 1, 3 ) = -1
42 math_Matrix ( 1, 4 ) = 2
43 math_Matrix ( 2, 1 ) = -5
44 math_Matrix ( 2, 2 ) = 1
45 math_Matrix ( 2, 3 ) = 3
46 math_Matrix ( 2, 4 ) = -4
47 math_Matrix ( 3, 1 ) = 2
48 math_Matrix ( 3, 2 ) = 0
49 math_Matrix ( 3, 3 ) = 1
50 math_Matrix ( 3, 4 ) = -1
51 math_Matrix ( 4, 1 ) = 1
52 math_Matrix ( 4, 2 ) = -5
53 math_Matrix ( 4, 3 ) = 3
54 math_Matrix ( 4, 4 ) = -3
55
56 Determinant of Matrix D: 40
57 Inverse of the Matrix E:
58 math_Matrix of RowNumber = 3 and ColNumber = 3
59 math_Matrix ( 1, 1 ) = -2
60 math_Matrix ( 1, 2 ) = 1
61 math_Matrix ( 1, 3 ) = -8.88178e-017
62 math_Matrix ( 2, 1 ) = -6.5
63 math_Matrix ( 2, 2 ) = 3
64 math_Matrix ( 2, 3 ) = -0.5
65 math_Matrix ( 3, 1 ) = -16
66 math_Matrix ( 3, 2 ) = 7
67 math_Matrix ( 3, 3 ) = -1
68
69 Inverse of the Matrix F:
70 math_Matrix of RowNumber = 4 and ColNumber = 4
71 math_Matrix ( 1, 1 ) = 1
72 math_Matrix ( 1, 2 ) = -2
73 math_Matrix ( 1, 3 ) = 0
74 math_Matrix ( 1, 4 ) = 0
75 math_Matrix ( 2, 1 ) = -2
76 math_Matrix ( 2, 2 ) = 5
77 math_Matrix ( 2, 3 ) = -0
78 math_Matrix ( 2, 4 ) = -0
79 math_Matrix ( 3, 1 ) = 0
80 math_Matrix ( 3, 2 ) = 0
81 math_Matrix ( 3, 3 ) = 2
82 math_Matrix ( 3, 4 ) = -3
83 math_Matrix ( 4, 1 ) = -0
84 math_Matrix ( 4, 2 ) = -0
85 math_Matrix ( 4, 3 ) = -5
86 math_Matrix ( 4, 4 ) = 8
87
88 Press any key to continue . . .
線性方程組的計(jì)算方法請(qǐng)參考另一篇blog:
使用OpenCASCADE的Math功能解線性方程組
http://m.shnenglu.com/eryar/archive/2012/06/21/179629.html
四、結(jié)論 Conclusion
OpenCascade的math_Matrix實(shí)現(xiàn)了矩陣的大部分運(yùn)算,也可以作為一個(gè)小型的C++矩陣計(jì)算庫來使用,在沒有安裝Matlab、Mathematica等軟件的情況下,可以使用這個(gè)庫進(jìn)行一些計(jì)算。
另外,對(duì)《計(jì)算方法》中算法感興趣的讀者可以參考OpenCascade其中代碼的實(shí)現(xiàn),加深對(duì)相關(guān)算法的理解。
五、參考文獻(xiàn) Bibliography
1. 同濟(jì)大學(xué)應(yīng)用數(shù)學(xué)系 線性代數(shù) 高等教育出版社 2003
2. 易大義,沈云寶,李有法 計(jì)算方法 浙江大學(xué)出版社 2002