我的SICP習題答案(1.10)
首先,可以寫出這個函數的函數式:
那么,對于 f(0,n), n>=0
當 n >= 1 時, f(0,n) = 2n ,
而當 n = 0 時, f(0,0) = 0 = 2*0, 也滿足 2n ,
故 f(0,n) = 2n, n>=0.
對于f(1,n), n>=1
當 n > 1 時,有 f(1,n) = f(0, f(1, n-1)) = 2*f(1,n-1),
設 f(1,n) = 2^n
if n = 1, f(1,1) = 2 = 2^1
when n > 1, if f(1,n-1) = 2^(n-1)
then f(1,n) = 2*f(1,n-1) = 2*(2^(n-1)) = 2^n
故 f(1,n) = 2^n, n>0.
對于f(2,n), n>0
if n > 1 ,then f(2,n) = f(1, f(2, n-1)) = 2^f(2,n-1),
設 f(2,n) = 2^(2^(... (n 個 2)
if n = 1, then f(2,1) = 2
when n > 1, if f(2, n-1) = 2^(2^(... (n-1)
then f(2,n) = 2^f(2,n-1) = 2^(2^(
這樣我們對于 (A 1 10) = 2^10 = 1024, (A 2 4) = 2^(2^(2^2)) = 2^16 = 65536
而 (A 3 3) = (A 2 A(3 2)) = A(2 A(2 A(2 1))) = (A 2 4) = 2^16 = 65536
(f n) = (A 0 n) = 2n
(g n) = (A 1 n) = 2^n
(h n) = (A 2 n) = 2^(2^(... (n個2)
---------------------------------------------
在網上可以找到關于 Ackermann 函數的討論,主要是針對這個雙遞歸如何用迭代來實現,Ackermann 函數是 德國數學家W.Ackermann 在1928年提出的。在 WikiPedia 英文版上可以搜索 Ackermann function 詞條,有詳細介紹,不過這個Ackermann function 略有不同。如下圖:
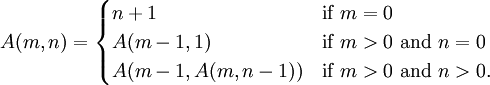
0, y = 0;
f(x,y) = 2y, x = 0;
2, y = 1;
f(x-1, f(x, y-1));
f(x,y) = 2y, x = 0;
2, y = 1;
f(x-1, f(x, y-1));
那么,對于 f(0,n), n>=0
當 n >= 1 時, f(0,n) = 2n ,
而當 n = 0 時, f(0,0) = 0 = 2*0, 也滿足 2n ,
故 f(0,n) = 2n, n>=0.
對于f(1,n), n>=1
當 n > 1 時,有 f(1,n) = f(0, f(1, n-1)) = 2*f(1,n-1),
設 f(1,n) = 2^n
if n = 1, f(1,1) = 2 = 2^1
when n > 1, if f(1,n-1) = 2^(n-1)
then f(1,n) = 2*f(1,n-1) = 2*(2^(n-1)) = 2^n
故 f(1,n) = 2^n, n>0.
對于f(2,n), n>0
if n > 1 ,then f(2,n) = f(1, f(2, n-1)) = 2^f(2,n-1),
設 f(2,n) = 2^(2^(... (n 個 2)
if n = 1, then f(2,1) = 2
when n > 1, if f(2, n-1) = 2^(2^(... (n-1)
then f(2,n) = 2^f(2,n-1) = 2^(2^(
這樣我們對于 (A 1 10) = 2^10 = 1024, (A 2 4) = 2^(2^(2^2)) = 2^16 = 65536
而 (A 3 3) = (A 2 A(3 2)) = A(2 A(2 A(2 1))) = (A 2 4) = 2^16 = 65536
(f n) = (A 0 n) = 2n
(g n) = (A 1 n) = 2^n
(h n) = (A 2 n) = 2^(2^(... (n個2)
---------------------------------------------
在網上可以找到關于 Ackermann 函數的討論,主要是針對這個雙遞歸如何用迭代來實現,Ackermann 函數是 德國數學家W.Ackermann 在1928年提出的。在 WikiPedia 英文版上可以搜索 Ackermann function 詞條,有詳細介紹,不過這個Ackermann function 略有不同。如下圖:
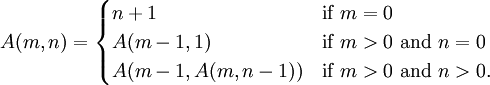
posted on 2008-03-11 23:33 cuigang 閱讀(1504) 評論(0) 編輯 收藏 引用 所屬分類: Lisp/Scheme 、我的SICP答案


