https://blog.csdn.net/u014652390/article/details/79139010
一、圖像坐標：我想和世界坐標談談(A)
玉米竭力用輕松具體的描述來講述雙目三維重建中的一些數學問題。希望這樣的方式讓大家以一個輕松的心態閱讀玉米的《計算機視覺學習筆記》雙目視覺數學架構系列博客。這個系列博客旨在捋順一下已標定的雙目視覺中的數學主線。數學推導是有著幾分枯燥的，但奇妙的計算機視覺世界是建立在嚴密的數學架構之上的。所以對數學框架的理解是理解雙目視覺的必由之路。不過請大家放心，接下來玉米會以盡量有趣，盡量更接地氣兒的方式，闡釋一下自己對雙目視覺數學或者說是投影幾何的理解。
先來張《計算機視覺：算法與應用》中的3D重建示例圖鎮樓！
好吧，現在言歸正傳，來看看幾何學上世界是怎樣投影進攝相機里的吧！接下來讓我們來看一下本系列博客的第一“搏”：
圖像坐標：我想和世界坐標談談(A)
首先，我先解釋一下這個題目吧。題目的字面意義是說：圖像坐標系想和世界坐標系談談。這里面包含著兩個問題：
A、談話對象：視覺系統的三大坐標系：世界坐標系，攝像機坐標系和圖像坐標系。這是玉米在本文《我想和世界坐標談談 (A)》中想要和大家分享的內容。其中主要包含：三大坐標系的位置、作用和應用場景。
B、談話方式：兩個不同的坐標系之間該如何溝通呢？玉米將在《我想和世界坐標談談(B)》中和大家分享一下剛體變換和透視 投影變換。連起兩個坐標系之間這不在一個參考系的“世界上最遠的距離”。
好吧，下面讓我們來揭開三大坐標系的廬山真面目。
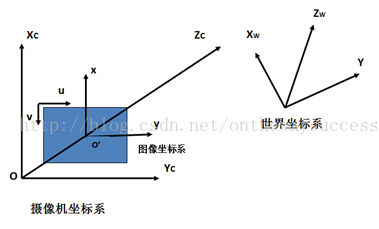
上圖是三個坐標的示意簡圖，通過它大家可以對三個坐標有一個直觀的認識。下面來看看三個坐標系的骨子里藏了什么。
世界坐標系（XW,YW,ZW）：其是目標物體位置的參考系。除了無窮遠，世界坐標可以根據運算方便與否自由放置。在雙目視覺中世界坐標系主要有三個用途：1、標定時確定標定物的位置2、作為雙目視覺的系統參考系，給出兩個攝像機相對世界坐標系的關系，從而求出相機之間的相對關系3、作為重建得到三維坐標的容器，盛放重建后的物體的三維坐標。世界坐標系是將看見中物體納入運算的第一站。
攝像機坐標系(XC,YC,ZC)：其是攝像機站在自己角度上衡量的物體的坐標系。攝像機坐標系的原點在攝像機的光心上，z軸與攝像機光軸平行。它是與拍攝物體發生聯系的橋頭堡，世界坐標系下的物體需先經歷剛體變化轉到攝像機坐標系（旋轉和平移），然后再和圖像坐標系發生關系。它是圖像坐標與世界坐標之間發生關系的紐帶，溝通了世界上最遠的距離。哈哈
圖像坐標系(x,y)米/(u,v)像素 :其是以攝像機拍攝的二維照片為基準建立的坐標系。用于指定物體在照片中的位置。玉米更傾向將(x,y)稱為連續圖像坐標或空間圖像坐標，將(u,v)稱為離散圖像坐標系或者是像素圖像坐標系（雖然這樣的稱呼未經考證，但更能傳達二者的物理意義）。
(x,y)坐標系的原點位于攝像機光軸與成像平面的焦點O’(u0,v0)上，單位為長度單位(米)。(u,v)坐標系的原點在圖片的左上角（其實是存儲器的首地址）如上圖所示，單位為數量單位(個)。(x,y)主要用于表征物體從攝像機坐標系向圖像坐標系的透視投影關系。而(u,v)則是實實在在的，我們能從攝像機中得到的真實信息。
(x,y)與(u,v)存在如下轉換關系：
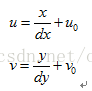
dx代表x軸方向一個像素的寬度，dy代表y軸方向上一個像素的寬度。dx、dy為攝像機的內參數。(u0,v0)稱為圖像平面的主點，也是攝像機的內參數。其實相當于對x軸和y軸的離散化。其可以運用齊次坐標，將上式寫成矩陣形式，如下：
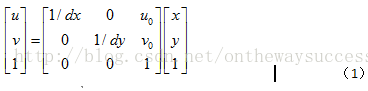
（1）式運用了齊次坐標，初學者可能會感到有些迷惑。大家會問：怎樣將普通坐標轉換為齊次坐標呢？齊次坐標能帶來什么好處呢？
玉米在這里對齊次坐標做一個通俗的解釋。此處只講怎么將普通坐標改寫為齊次坐標及為什么引入齊次坐標。這里只做一個通俗但不太嚴謹的表述。力求簡單明了。針對齊次坐標的嚴謹的純數學推導，可參見“周興和版的《高等幾何》---1.3拓廣平面上的齊次坐標”。玉米曾詳細讀過《高等幾何》這本書，但覺得離計算機視覺有點遠，是講純數學的投影關系的，較為生澀難懂。
齊次坐標可以理解為在原有坐標后面加一個“小尾巴”。將普通坐標轉換為齊次坐標，通常就是在增加一個維度，這個維度上的數值為1。如圖像坐標系(u,v)轉換為(u,v,1)一樣。對于無窮遠點，小尾巴為0。注意，給零向量增加小尾巴，數學上無意義。
那么，為什么計算機視覺在坐標運算時要加上這個“小尾巴”呢？
玉米看來有兩點原因：
1、 將投影平面擴展到無窮遠點。如對消隱點(vanishing point)的描述。
2、 使得計算更加規整
如式（1）如果用普通坐標來表達的話，會是下面的樣子：
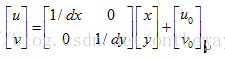
這樣的運算形式會給后與運算帶來一定的麻煩，所以齊次坐標是一個更好的選擇。
齊次坐標還有一個重要的性質，伸縮不變性。即：設齊次坐標M，則αM=M。
玉米才疏學淺，筆記中如有紕漏指出，希望大家不吝指出。玉米在這里拜謝啦！
二、圖像坐標：我想和世界坐標談談(B)
玉米將在這篇博文中，對圖像坐標與世界坐標的這場對話中涉及的第二個問題：談話方式，進行總結。世界坐標是怎樣變換進攝像機，投影成圖像坐標的呢？
玉米做了一個簡單的圖示，在這里做一個提綱。圖中顯示，世界坐標系通過剛體變換到達攝像機坐標系，然后攝像機坐標系通過透視投影變換到達圖像坐標系。可以看出，世界坐標與圖像坐標的關系建立在剛體變換和透視投影變換的基礎上。為了獎勵剛體變和透視投影變換溝通了“世界上最遠的距離”，玉米在圖上獎勵了他們兩朵小紅花。哈哈
首先，讓我們來看一下剛體變換是如何將世界坐標系與圖像坐標系聯系起來的吧。這里，先對剛體變換做一個介紹：
剛體變換(regidbody motion):三維空間中， 當物體不發生形變時，對一個幾何物體作旋轉， 平移的運動，稱之為剛體變換。
因為世界坐標系和攝像機坐標都是右手坐標系，所以其不會發生形變。我們想把世界坐標系下的坐標轉換到攝像機坐標下的坐標，如下圖所示，可以通過剛體變換的方式。空間中一個坐標系，總可以通過剛體變換轉換到另外一個個坐標系的。轉一轉，走一走，就到另外一個坐標系下了。以前可能是面朝大海，經過平移旋轉，最終可能只能面朝冰山了，哈哈
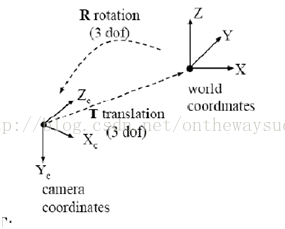
下面讓我來看一下，二者之間剛體變化的數學表達。
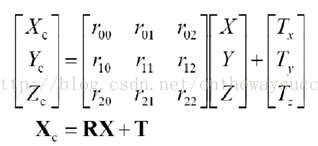
其中，XC代表攝像機坐標系，X代表世界坐標系。R代表旋轉，T代表平移。R、T與攝像機無關，所以稱這兩個參數為攝像機的外參數(extrinsic parameter)可以理解為兩個坐標原點之間的距離，因其受x,y,z三個方向上的分量共同控制，所以其具有三個自由度。
R則為分別繞XYZ三軸旋轉的效果之和。如下面所示：
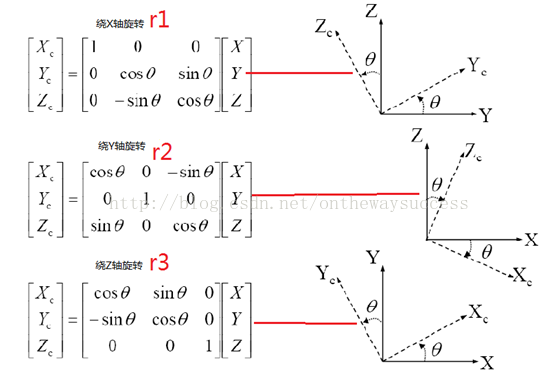
R=r1*r2*r3.其由三個方向的θ控制，故具有三個自由度。
好了，剛體變換就講完了。大家應該都了解，世界坐標系到攝像機坐標系之間的轉換過程了吧。
接下來，讓我們看看攝像機坐標下的坐標如何投影到圖像坐標系下，最終變為照片中的一個像素。這其中包含兩個過程：一是從攝像機坐標到“空間圖像坐標”（x,y）所發生的透視投影；二是從“連續圖像坐標”到“離散圖像坐標”(u,v)。后者我們已經在第一篇博文中解釋過。所以在這里，主要介紹一下透視投影。
透視投影(perspective projection): 用中心投影法將形體投射到投影面上，從而獲得的一種較為接近視覺效果的單面投影圖。有一點像皮影戲。它符合人們心理習慣，即離視點近的物體大，離視點遠的物體小，不平行于成像平面的平行線會相交于消隱點(vanish point)。
啰嗦這么多，其實大家看看示意圖，看看公式，秒懂。
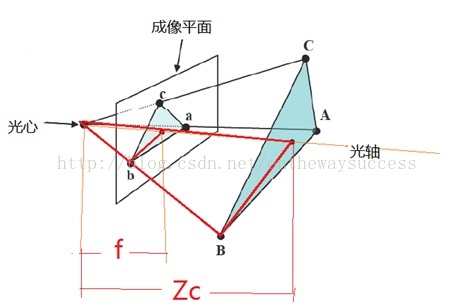
以圖中B(XB,YB)點為例，在小孔成像攝像機模型下（幾何分析的最常用模型）。這里的f為攝像機的焦距，其屬于攝像機的內參數(intrinsic parameter)。其在成像平面上的投影點b(xb,yb)的坐標利用簡單的相似三角形比例關系很容易求出：
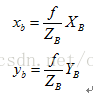
上面兩式也闡明了攝像機坐標與圖像坐標之間的透視投影關系。
好吧，現在玉米已經把圖像坐標與世界坐標之間的這場對話所需經歷的三個波折的過程加以了解釋。即：剛體變換、透視投影、(x,y)換(u,v)（ps.這個在上一篇博文中講過）。接下來玉米用一張圖把三個過程連接起來。實現從世界坐標(X,Y,Z)到(u,v)之間的轉換。讓圖像坐標與世界坐標直接對話。
下圖中的轉換關系，都是用齊次坐標表達的，大家會發現這樣的表達非常整潔。
其實這張圖顯示的過程還有一個名字：攝像機模型(camera model)。其實也就是攝像機的幾何模型了。
將三者相乘，可以把這三個過程和在一起，寫成一個矩陣：
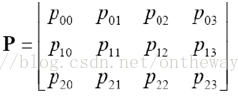
P就是世界坐標到圖像坐標的直接聯系人，P就表示了一個投影相機，有下面公式：
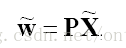
注意在表示齊次坐標時，需要在符號上面加個小帽子。除去齊次坐標控制位P23，P具有11個自由度。
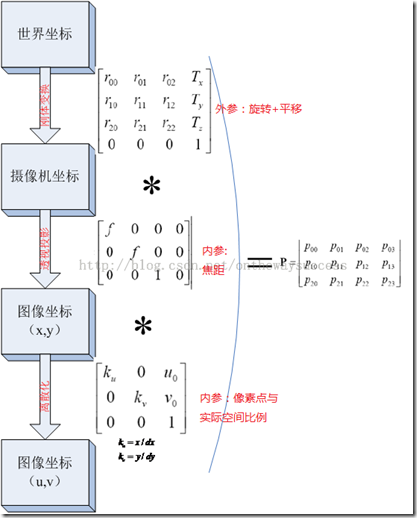
攝像機模型及其中涉及的坐標系等，是弄清3D重建幾何框架的基礎。可以把它們視為基本運算關系。后面對于三維重建幾何框架的推導，都是要用到三個基本坐標系和攝像機模型的。
到這里玉米就順利搭建起了圖像坐標與世界坐標間的這場對話。如有紕漏還請大家擔待，并指正！
三、致敬“張正友標定”
此處“張正友標定”又稱“張氏標定”，是指張正友教授于1998年提出的單平面棋盤格的攝像機標定方法。張氏標定法已經作為工具箱或封裝好的函數被廣泛應用。張氏標定的原文為“A Flexible New Technique forCamera Calibration”。此文中所提到的方法，為相機標定提供了很大便利，并且具有很高的精度。從此標定可以不需要特殊的標定物，只需要一張打印出來的棋盤格。So great! 這樣的方法讓人肅然起敬。所以玉米的這篇博客的題目是：致敬“張氏標定”。
當然，此博的內容也是圍繞著“張氏標定”進行的，在這里，玉米主要介紹一下，“張氏標定”的數學思路。因為標定在整個基于標定攝像機的三維重建的幾何過程占有最重要最核心的地位。如下圖：
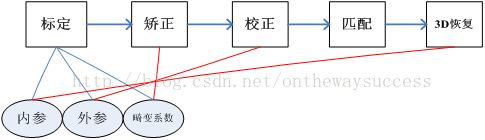
從圖中明顯可以看出，標定得到的內參、外參和畸變系數，是雙目視覺進行圖片矯正，攝像機校正和3D恢復的基礎。沒有好的標定，雙目視覺系統就無法完成3D重建。
既然標定對雙目視覺如此重要，我們有必要對數學的深層含義多加理解。以張氏標定為例，讓我們挖開工具箱，看看其數學本質吧。因為張教授的論文中對標定方法的講述是循序漸進的，所以玉米在這里將按照張教授論文中的順序，為大家講述一下，張氏標定的脈絡。
1、標定平面到圖像平面的單應性
因為張氏標定是一種基于平面棋盤格的標定，所以想要搞懂張氏標定，首先應該從兩個平面的單應性(homography)映射開始著手。
單應性(homography)：在計算機視覺中被定義為一個平面到另一個平面的投影映射。首先看一下，圖像平面與標定物棋盤格平面的單應性。
由上兩篇博文中講到的攝像機模型，肯容易得到：
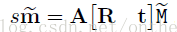
其中m的齊次坐標表示圖像平面的像素坐標(u,v,1)，M的齊次坐標表示世界坐標系的坐標點(X,Y,Z,1)。A[R t]即是上面一篇博客推出的P。R表示旋轉矩陣、t表示平移矩陣、S表示尺度因子。A表示攝像機的內參數,具體表達式如下：
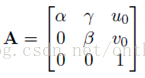
α=f/dx，β=f/dy,因為像素不是規規矩矩的正方形，γ代表像素點在x,y方向上尺度的偏差。
這里還有一個“梗兒”，就是S。它只是為了方便運算，對于齊次坐標，尺度因子不會改變坐標值的。
因為標定物是平面，所以我們可以把世界坐標系構造在Z=0的平面上。然后進行單應性計算。令Z=0可以將上式轉換為如下形式：
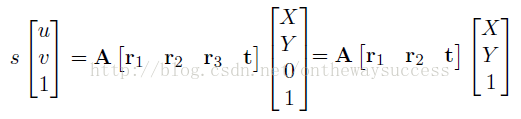
既然，此變化屬于單應性變化。那么我們可以給A[r1 r2 t]一個名字：單應性矩陣。并記H= A[r1 r2 t]。
那么現在就有：
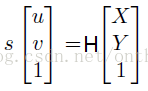
大家可以分析一下，H是一個三3*3的矩陣，并且有一個元素是作為齊次坐標。因此，H有8個未知量待解。
(x,y)作為標定物的坐標，可以由設計者人為控制，是已知量。(u,v)是像素坐標，我們可以直接通過攝像機獲得。對于一組對應的(x,y)-à(u,v)我們可以獲得兩組方程。
現在有8個未知量需要求解，所以我們至少需要八個方程。所以需要四個對應點。四點即可算出，圖像平面到世界平面的單應性矩陣H。
這也是張氏標定采用四個角點的棋盤格作為標定物的一個原因。
在這里，我們可以將單應性矩陣寫成三個列向量的形式，即：
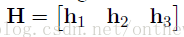
2、利用約束條件求解內參矩陣A
從上面可知，應用4個點我們可以獲得單應性矩陣H。但是，H是內參陣和外參陣的合體。我們想要最終分別獲得內參和外參。所以需要想個辦法，先把內參求出來。然后外參也就隨之解出了。我們可以仔細的“觀摩”一下下面的式子。
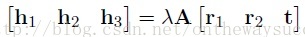
從中可以得出下面兩個約束條件，這兩個約束條件都是圍繞著旋轉向量來的。
1、r1,r2正交 得：r1r2=0。這個很容易理解，因為r1,r2分別是繞x,y軸旋轉的。應用高中立體幾何中的兩垂直平面上（兩個旋轉向量分別位于y-z和x-z平面）直線的垂直關系即可輕松推出。
2、旋轉向量的模為1，即|r1|=|r2|=1。這個也很容易理解，因為旋轉不改變尺度嘛。如果不信可以回到上一篇博客，找到個方向的旋轉矩陣化行列式算一下。
通過上面的式子可以將r1,r2代換為h1,h2與A的組合進行表達。即 r1=h1A-1，r2=h2A-1.根據兩約束條件，可以得到下面兩個式子：
大家從上面兩個式子是不是看出一點端倪了。式子中，h1,h2是通過單應性求解出來的那么未知量就僅僅剩下，內參矩陣A了。內參陣A包含5個參數：α，β，u0，v0，γ。那么如果我們想完全解出這五個未知量，則需要3個單應性矩陣。3個單應性矩陣在2個約束下可以產生6個方程。這樣可以解出全部的五個內參了。大家想一下，我們怎樣才能獲得三個不同的單應性矩陣呢？答案就是，用三幅標定物平面的照片。我們可以通過改變攝像機與標定板間的相對位置來獲得三張不同的照片。（當然也可以用兩張照片，但這樣的話就要舍棄掉一個內參了γ=0）
到這里，大家應該就明白我們在張氏標定法時為什么要不斷變換標定板的方位了吧。當然這只是一個原因。第二個原因，玉米會在講極大似然時講到。
下面在對我們得到的方程做一些數學上的變化，這些變化都是簡單的運算變化了，相信大家動動筆，一算就可以算出。這些變化都是為了運算方便的，所以也沒什么物理意義。
首先令：
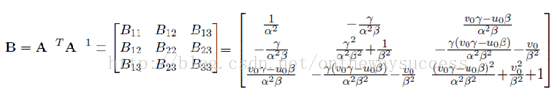
很容易發現B是一個對稱陣，所以B的有效元素只剩下六個（因為有三對對稱的元素是相等的，所以只要解得下面的6個元素就可以得到完整的B了），讓這六個元素構成向量b。
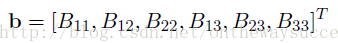
接下來在做一步純數學化簡：
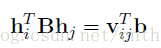
可以計算得：
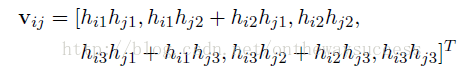
利用約束條件可以得到下面，方程組：
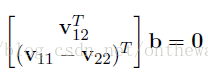
這個方程組的本質和前面那兩個用h和A組成的約束條件方程組是一樣的。在此重復一遍解釋：如果我們想完全解出這五個未知量，則需要3個單應性矩陣。3個單應性矩陣在2個約束下可以產生6個方程。這樣可以解出全部的五個內參了。大家想一下，我們怎樣才能獲得三個不同的單應性矩陣呢？答案就是，用三幅標定物平面的照片。我們可以通過改變攝像機與標定板間的相對位置來獲得三張不同的照片。（當然也可以用兩張照片，但這樣的話就要舍棄掉一個內參了γ=0）
通過至少含一個棋盤格的三幅圖像，應用上述公式我們就可以估算出B了。得到B后，我們通過cholesky分解 ，就可以輕松地得到攝像機的內參陣A。
3、基于內參陣估算外參陣
通過上面的運算，我們已經獲得了攝像機的內參陣。那么對于外參陣，我們很容易通過下面的公式解得：
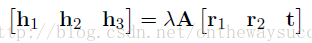
對上面公式進行化簡，可以得到：
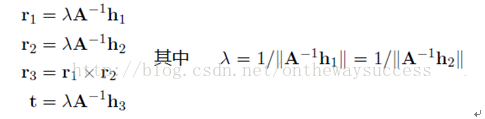
至此，玉米已經將張氏標定的主體數學框架已經講完了。介于篇幅關系（怕太長大機會讀的昏昏欲睡，哈哈）。但其實我們做了這么多推導，僅僅是為后面的極大似然參數估計提供初值。但當然這個初值也是不可或缺的，因為沒有這個初值，就無法估計出更為準確的參數。玉米將張氏標定中用于提高標定精度的極大似然算法，放到下一篇博客中進行講解。
還是老話：玉米才疏學淺，講解之中難免有紕漏，請大家諒解，并指正。
四、極大似然參數估計
此篇博文，玉米將和大家分享一下“張氏標定”除幾何推導外的另外一大精髓：參數估計。
張教授在大作“A Flexible New Technique for Camera Calibration”中的原話如下：” The above solution is obtained through minimizing an algebraic distancewhich is not physically meaningful. We can refine it through maximum likelihoodinference”.意思是：上面的幾何推導僅僅是純代數上的擬合，沒有物理意義。下面讓我們通過極大似然理論對得到的結果進行改善。
順著張教授的意思，玉米先在這里為大家從概念上講述一下極大似然估計。
極大似然估計是一種估計總體未知參數的方法。它主要用于點估計問題。所謂點估計是指用一個估計量的觀測值來估計未知參數的真值。說穿了就一句話：就是在參數空間中選取使得樣本取得觀測值的概率最大的參數。
我們定義似然函數：
總體分布為離散型的：（p是已知的分布律）
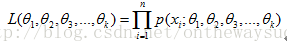
總體分布為連續性的：（f為概率密度函數）
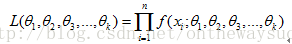
極大似然法就是在的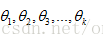
可取范圍內，挑選出來的使L達到最大的未知參數的估計值
。
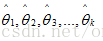如果在內：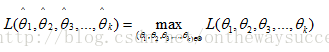
，那么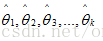就稱為極大似然估計值。
列了這么一大圈兒概念，估計大家看的都昏昏入睡了。玉米在這里用通俗點兒的方式解釋一下極大似然估計：
對很多實驗，我們可以觀察到樣本，但影響樣本的參數卻是未知的。那我們就得對樣本進行估計。既然我們要去估計，那么就想要估計的準。極大似然法就只在概率分布的觀念下，指導我們估計的更準的方法。現實世界中，存在著一條普遍規律：與現實相差越遠的概率越小。這就相當于人群中，非主流總是比主流要少一樣，偏差大的總是占少數。所以，可能發生的概率越大就會越接近真實值。極大似然法就是應用這種思想，認為可能性最大的就是最優的估計值。即極大似然估計值就是最接近真實值的參數值。
那么，極大似然為什么有這么一個別致的名字呢？什么是似然呢？是因為估計值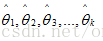不是隨機變量，所以不能把它的可能性稱為概率，那么數學家們就想了這樣(likelihood)一個名字來代表可能性。
極大似然法的一些概念上的問題玉米就講到這里了。下面然玉米帶這大家分析一個具體問題：張教授在張氏標定法中所用的極大似然估計。
首先來看一下，為什么標定的內外參數可以用極大似然法進行估計：
因為我們是假定圖像上的角點是被噪聲干擾的，且我們認為這些噪聲是高斯噪聲。那么對于噪聲的幅度就是給觀測值造成的誤差。但高斯噪聲的概率密度我們是已知的，所以我們可以用前面所述的極大似然估計的思想去“猜”真值。
那么接下來我們就需要構造一個似然函數，然后尋找其最大值了。張教授在文章中直接略過推導，直接給出了公式：
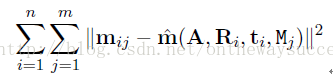
說當此式取得最小值時，就是參數的最大似然估計值。
玉米在這里為大家講一下自己的理解：
設，角點附近的噪聲服從高斯分布
則：角點mij的樣本值服從如下，概率密度函數：
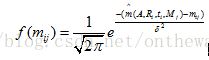
現在構造，似然函數：
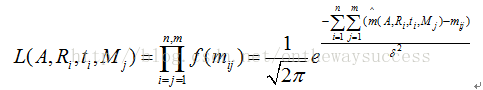
現在讓L取得最大值，則可令下式最小：
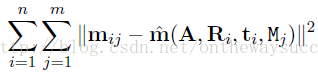
那么怎么令上面這個目標函數達到最小值呢，張氏標定法運用了可以用來解決多參數非線性系統優化問題的Levenberg-Marquardt算法。對于該方法，詳細的介紹大家可以參照《The levenberg-marquardt algorithm, implementation andtheory》一文進行深入了解。這里給出下載本文的鏈接：
http://link.springer.com/chapter/10.1007%2FBFb0067700
那么張氏標定法在不考慮鏡頭畸變的情況下的，獲取攝像機內外參數的數理推導過程。玉米就為大家講到這里了。下面一篇博文，玉米會給大家分析一下，張氏標定法是怎樣分析攝像機的非線性畸變的。
還是老話：玉米才疏學淺，講解之中難免有紕漏，請大家諒解，并指正。
六、張正友標定法小結
這一博文，是玉米后補上的。因為覺得前面用了三篇博文來描述張氏標定法，略顯散亂。在這里總結一下，使條理清晰一點。另外關于張氏標定所得參數也還有兩點需要澄清。下面這個總結，其實也是在“A Flexible New Technique forCamera Calibration”中出現的。
一、張氏標定的過程：
1. 打印一張棋盤格，把它貼在一個平面上，作為標定物。
2. 通過調整標定物或攝像機的方向，為標定物拍攝一些不同方向的照片。
3. 從照片中提取特征點（如角點）。
4. 估算理想無畸變的情況下，五個內參和所有外參。
5. 應用最小二乘法估算。實際存在徑向畸變下的畸變系數。
6. 極大似然法，優化估計，提升估計精度。
通過這樣的過程，我們就獲得了具有高估計精度的五個內參，三個外參和兩個畸變系數。利用這些信息，我們可以進行畸變矯正、圖像校正和最終的三維信息恢復。
二、以下是對于張氏標定求得的內參，需要注意的一點：
通過張氏標定，我們并不能得到：焦距(f)和像素的物理尺寸(sx,sy)兩個參數。因為我們在求解內參陣A時，求解出的是α和β。
α=f/ sx,β= f/ sy 。分別代表焦距長度上，x軸和y軸像素的個數。
雖然，沒有求得焦距，但這并不影響，我們在三維坐標恢復時，進行三角運算。因為彼時，我們的計算中用到的也是α和β。
大家可能會有疑問，既然我們無法得到焦距(f)和像素的物理尺寸(sx,sy)兩個參數。那么在opencv中，調用的cvCalibrateCamera2時返回的參數中是包含焦距(f)的。Opencv的這個函數也是用了張氏標定法。為什么可以得到f呢？
答案是這條opencv函數對內參陣做了簡化，其認為γ=0即像素的物理尺寸(sx,sy)兩個參數相等。然后統一約掉物理尺寸s。得到的B陣如下：
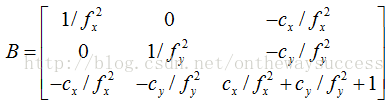
這樣我們就可以解出f了。
張氏標定的精確度可達到0.5個像素，這樣的指標已經可以滿足絕大多數的應用了。所以如此簡單的方法，得到了這么高的精度。這樣的方法是值得人們膜拜的。在此，在次向張正友教授致敬！
在此，玉米又對張氏標定法進行了一個總結。張氏標定的原理分析就到此為止了。但是它的作用還會延續到下面兩篇博文中。
玉米才疏學淺，文中如有紕漏，請大家批評指正。
七、立體標定與立體校正
這篇博文中，讓玉米和大家一起了解一下，張氏標定是怎樣過渡到立體標定的？在這里主要以雙目立體視覺進行分析。對于雙目立體視覺，我們有兩個攝像頭。它們就像人的一雙眼睛一樣，從不同的方向看世界。兩只眼睛中的圖像的視差，讓我們對世界有了三維的認識。
那么，想要知道視差，首先應該知道雙目視覺系統中兩個攝像頭之間的相對位置關系。我們可以通過同時對兩個攝像頭進行標定，分別得到二者相對同一坐標系的旋轉矩陣和平移矩陣。獲得這兩個矩陣的過程，就是立體標定的過程。也即是：從張氏標定走向立體標定！
兩攝像頭之間的旋轉矩陣和平移矩陣可以由下式求出：
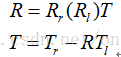
其中，R為兩攝像頭間的旋轉矩陣，T為兩攝像頭間的平移矩陣。Rr為右攝像頭經過張氏標定得到的相對標定物的旋轉矩陣，Tr為右攝像頭通過張氏標定得到的相對標定物的平移向量。Rl為左攝像頭經過張氏標定得到的相對相同標定物的旋轉矩陣，Tl為左攝像頭經過張氏標定得到的相對相同標定物的平移向量。
兩個式子是可以通過數學代換推導來的。但玉米覺得對這樣有明顯物理意義并且空間過程簡單的計算式。物理上的空間想象，比純代數代換，要生動的多。并且有利于大家揣摩整個物理過程。
在玉米眼里，這兩個式子是這樣的：
對于R，首先用T把左攝像機坐標系平移到右攝像機坐標系上（即兩坐標系遠點重合）。然后在同一參考系下的兩個旋轉矩陣相乘，表示世界坐標先向右旋轉到Rr ，再向左旋轉Rl。那么兩次旋轉后得到的旋轉，就是有攝像機旋轉到左攝像機所需的旋轉矩陣R。
對于T，那就更容易理解了，先用R對左坐標系旋轉一下，把左右兩攝像機調成平行，然后直接平移向量相減，即得到。兩攝像機之間的平移向量T。
上面求得的R和T就是立體標定得到的參數了。
那么運用的立體標定所得的參數了，下一步我們該做什么呢？答案是：立體校正。
在介紹立體校正的具體方法之前，讓我們來看一下，為什么要進行立體校正？
因為當兩個圖像平面是完全共面行對準時，計算立體視差是最簡單的。但是，在現實的雙目立體視覺系統中，是不存在完全的共面行對準的兩個攝像機圖像平面的。所以我們要進行立體校正。立體校正的目的就是，把實際中非共面行對準的兩幅圖像，校正成共面行對準。如下面示意圖所示。（共面行對準是指：兩攝像機圖像平面在同一平面上，且同一點投影到兩個攝像機圖像平面時，應該在兩個像素坐標系的同一行）
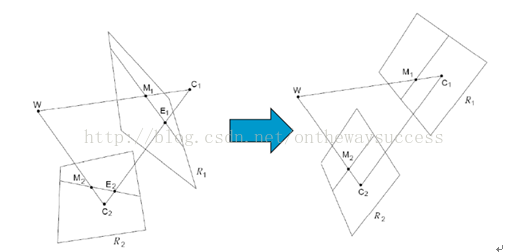
有了上述鋪墊，下面讓玉米給大家陳述一下基于立體標定所獲參數的立體校正的數學原理，或者說是幾何原理。但玉米在這里，主要和大家分享一下，如此校正的物理意義。
立體校正應該分兩步走：
1、 將兩個圖像平面拉回同一平面。
這一步，該怎么做呢？玉米相信，經過這么多鋪墊，大家應該早就心里有數了。這一步很簡單。可以這樣：兩個平面在方向上 之間不是相差一個旋轉矩陣R嗎，那么我們讓兩個相機個旋轉一半，但需注意二者的旋轉，應該是反向的。如下式所示：
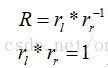
上面的這個公式是玉米根據物理意義自己總結的。rl 、rr 分別代表左攝像機和右攝像機為達到共面所需的旋轉矩陣。rl、rr程度 相同，但旋轉方向相反。左右相機分別經歷了這樣的旋轉之后，二者就已經共面了。大家應該明白了吧？
2、 旋轉圖像使得同行對準
玉米在這里先為大家展示一個，校正成功的圖吧。
大家可以像小學時候寫看圖說話作文一樣，觀察一下圖中校正前和校正后左右兩攝像機的圖像到底發生了什么本質的變 化。
玉米的答案是：左右兩圖分別繞光軸作了旋轉，旋轉過后兩攝像機的主點連線平行像素坐標的行線。
玉米的答案也是自己對行對準的理解，比較通俗。這與很多書上用極幾何術語描述的有些不同，大家可以思考一下，玉米 說的有沒有道理。
好，既然已經明確了，要達到行對準，圖像所需發生的變化。那么就讓我們用數學表達式來表達它們吧。
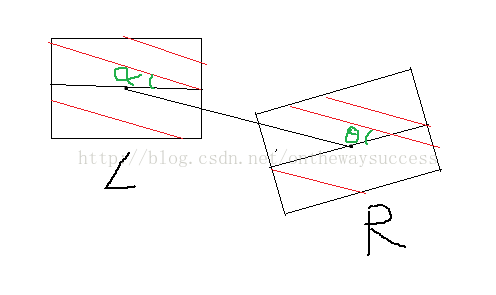
玉米畫了一個簡單的示意圖，畫的丑大家不要見笑。
紅色的線表示的是校正后的行線，其是左右對準的。大家可以看到，從原圖像的行線轉到校正后圖像的行線，左圖像轉動了α，右圖像轉動了θ。那么怎樣來確定兩個旋轉角度呢？
大家可以回憶一下，我們在本系列博文中的第二篇中講述剛體變換時，把旋轉矩陣按不同軸分解的方法。可以看做是沿光軸旋轉，旋轉目的是與主點連線平行。先以左圖像為例：
那么我們設旋轉矩陣為Rh ,
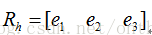
則Rh可以表示為以歸一化T（平移向量）：e1為旋轉的指針,則隨之e2為e1與光軸的叉積，e3為e2與e1的叉積：
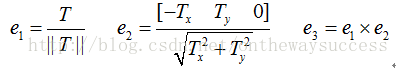
大家可以進一步算一下：
我們發現，其實行對準就是繞e3方向，轉了α。同樣的，對右圖就是轉了θ。
通過上面的推導，我們就把立體標定與立體校正中的數學思想理清楚了。其實，立體匹配是有很多種方法的，玉米在里只是介紹了立體校正的基本原理。其他方法中，有一些可以不依賴標定參數，如果大家想要對立體校正進行深入研究，大家可以搜索一些經典論文進行深入學習。如：A. Fusiello, E. Trucco, and A. Verri.寫的 Acompact algorithm for rectification of stereo pairs.等等
截止目前對于三維重建的所有準備工作，都已完成。幾何框架也僅剩下最后一步：立體成像。（因為本系列博文只介紹雙目視覺的幾何架構，所以跳過匹配不談）玉米在下一篇博文中將與大家分享一下，幾何脈絡的最終果實：立體成像。這也是我們對于雙目視覺幾何框架推導和理解的最終目標。
玉米才疏學淺，文中如有紕漏，請大家批評指正！
八、走向三維
我們前面花了七篇博文做鋪墊，我們所做的一切努力都是為了最后的這一擊——立體成像。因為玉米的這個系列文章是對雙目視覺幾何框架的總結。此處跳過匹配，假設左右圖像點的完美匹配的。只看在幾何上，三維坐標是如何被還原的。相對來說，最后的這一步，比前面是要輕松許多的，因為我們前面已經做了大量的工作。這些工作使得最后的這一步，由不可能稱為可能，由復雜變得簡單，吧啦吧啦。好吧，閑話少說，讓我們一起來見證這一時刻吧。
此處我們按opencv中cvcalibratecamera2()函數得到的焦距f進行三維坐標的求解。
請大家看下面示意圖（莫怪，玉米的圖一向畫的丑）：
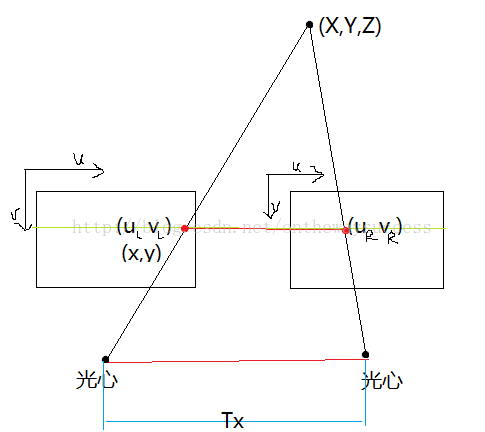
根據最簡單的相似三角形關系，我們就可以求出，物點坐標(X,Y,Z)。
首先，
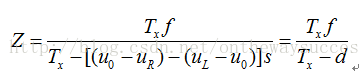
其中，s為像素的物理尺寸，d就是兩個攝像機間的視差，d=(uL-uR)s。
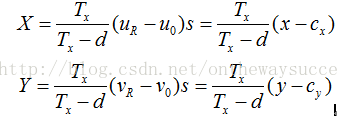
我們得到的這個三維坐標，相當于是在右攝像機的攝像機坐標系上的。
那么重建就是透視投影的逆過程，我們可以把這個過程表示成矩陣形式。我們定義Q為反投影矩陣。那么依照上式：
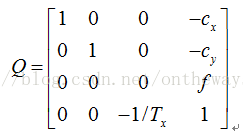
齊次坐標形式的三維坐標恢復，矩陣形式如下：
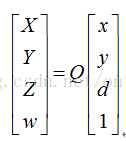
至此，玉米的《計算機視覺學習筆記》雙目視覺幾何框架系列文章順利收尾。希望這八篇博文對大家，尤其是計算機視覺的初學者有所幫助。
在行文過程中，玉米引用了網絡上的一些圖片，但大多找不到出處，所以未給出引用表。如這些圖片的主人，發現了自己的圖片在這個博客上，請和玉米聯系，玉米會將引用出處，重新給出！
本系列博文中涉及的數學運算頗多，玉米才疏學淺，中間若有理解上的錯誤，懇請大家批評指正！
原創地址：http://blog.csdn.net/onthewaysuccess/article/details/40709745