亚洲一区日韩,99精品国产高清一区二区,国产在线精品自拍

統計

隨筆 - 150
文章 - 1
評論 - 78
引用 - 0

常用鏈接

留言簿(27)

隨筆檔案(150)

文章檔案(1)

2006年1月 (1)

博客鏈接

baike.baidu.com
bbs.matwav.com
code.google.com/p
cs.cmu.edu/~quake
en.wikipedia.org
gamasutra.com
gamedev.net
k-3d.org/wiki
koders.com
mathworld.wolfram.com
netlib.org
osgchina.org
print.google.com
scribd.com
zh.wikipedia.com
友情鏈接

搜索

積分與排名

積分 - 291739
排名 - 91

貝塞爾曲線

LINK: http://zh.wikipedia.org/wiki/%E8%B2%9D%E8%8C%B2%E6%9B%B2%E7%B7%9A#.E9.9B.BB.E8.85.A6.E7.B9.AA.E5.9C.96

在數學的數值分析領域中，貝茲曲線（Bézier curve）是電腦圖形學中相當重要的參數曲線。更高維度的廣泛化貝茲曲線就稱作貝茲曲面，其中貝茲三角是一種特殊的實例。

貝茲曲線於1962年，由法國工程師皮埃爾·貝茲（Pierre Bézier）所廣泛發表，他運用貝茲曲線來為汽車的主體進行設計。貝茲曲線最初由 Paul de Casteljau 於1959年運用 de Casteljau 演算法開發，以穩定數值的方法求出貝茲曲線。

[編輯] 實例說明

[編輯] 線性貝茲曲線

給定點 P₀、P₁，線性貝茲曲線只是一條兩點之間的直線。這條線由下式給出：

$\mathbf{B}(t)=\mathbf{P}_0 + (\mathbf{P}_1-\mathbf{P}_0)t=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \mbox{ , } t \in [0,1]$

且其等同於線性插值。

[編輯] 二次方貝茲曲線

二次方貝茲曲線的路徑由給定點 P₀、P₁、P₂ 的函數 B(t) 追蹤：

$\mathbf{B}(t) = (1 - t)^{2}\mathbf{P}_0 + 2t(1 - t)\mathbf{P}_1 + t^{2}\mathbf{P}_2 \mbox{ , } t \in [0,1]$ 。

TrueType 字型就運用了以貝茲樣條組成的二次貝茲曲線。

[編輯] 三次方貝茲曲線

P₀、P₁、P₂、P₃ 四個點在平面或在三維空間中定義了三次方貝茲曲線。曲線起始於 P₀ 走向 P₁，並從 P₂ 的方向來到 P₃。一般不會經過 P₁ 或 P₂；這兩個點只是在那裡提供方向資訊。 P₀ 和 P₁ 之間的間距，決定了曲線在轉而趨進 P₃ 之前，走向 P₂ 方向的「長度有多長」。

曲線的參數形式為：

$\mathbf{B}(t)=\mathbf{P}_0(1-t)^3+3\mathbf{P}_1t(1-t)^2+3\mathbf{P}_2t^2(1-t)+\mathbf{P}_3t^3 \mbox{ , } t \in [0,1]$ 。

現代的成象系統，如 PostScript、Asymptote 和 Metafont，運用了以貝茲樣條組成的三次貝茲曲線，用來描繪曲線輪廓。

[編輯] 一般化

$n$ 階貝茲曲線可如下推斷。給定點 P₀、P₁、…、P_n，其貝茲曲線即

$\mathbf{B}(t)=\sum_{i=0}^n {n\choose i}\mathbf{P}_i(1-t)^{n-i}t^i =\mathbf{P}_0(1-t)^n+{n\choose 1}\mathbf{P}_1(1-t)^{n-1}t+\cdots+\mathbf{P}_nt^n \mbox{ , } t \in [0,1]$ 。

例如 $n = 5$ ：

$\mathbf{B}(t)=\mathbf{P}_0(1-t)^5+5\mathbf{P}_1t(1-t)^4+10\mathbf{P}_2t^2(1-t)^3+10\mathbf{P}_3t^3(1-t)^2+5\mathbf{P}_4t^4(1-t)+\mathbf{P}_5t^5 \mbox{ , } t \in [0,1]$ 。

如上公式可如下遞歸表達：用 $\mathbf{B}_{\mathbf{P}_0\mathbf{P}_1\ldots\mathbf{P}_n}$ 表示由點 P₀、P₁、…、P_n 所決定的貝茲曲線。則

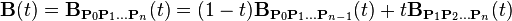
$\mathbf{B}(t) = \mathbf{B}_{\mathbf{P}_0\mathbf{P}_1\ldots\mathbf{P}_n}(t) = (1-t)\mathbf{B}_{\mathbf{P}_0\mathbf{P}_1\ldots\mathbf{P}_{n-1}}(t) + t\mathbf{B}_{\mathbf{P}_1\mathbf{P}_2\ldots\mathbf{P}_n}(t)$

用平常話來說， $n$ 階的貝茲曲線，即雙 $n - 1$ 階貝茲曲線之間的插值。

[編輯] 術語

一些關於參數曲線的術語，有

$\mathbf{B}(t) = \sum_{i=0}^n \mathbf{P}_i\mathbf{b}_{i,n}(t),\quad t\in[0,1]$

即多項式

$\mathbf{b}_{i,n}(t) = {n\choose i} t^i (1-t)^{n-i},\quad i=0,\ldots n$

又稱作 n 階的伯恩斯坦基底多項式，定義 0⁰ = 1。

點 P_i 稱作貝茲曲線的控制點。多邊形以帶有線的貝茲點連接而成，起始於 P₀ 並以 P_n 終止，稱作貝茲多邊形（或控制多邊形）。貝茲多邊形的凸包（convex hull）包含有貝茲曲線。

[編輯] 註解

開始於 P₀ 並結束於 P_n 的曲線，即所謂的端點插值法屬性。
曲線是直線的充分必要條件是所有的控制點都位在曲線上。同樣的，貝茲曲線是直線的充分必要條件是控制點共線。
曲線的起始點（結束點）相切於貝茲多邊形的第一節（最後一節）。
一條曲線可在任意點切割成兩條或任意多條子曲線，每一條子曲線仍是貝茲曲線。
一些看似簡單的曲線（如圓）無法以貝茲曲線精確的描述，或分段成貝茲曲線（雖然當每個內部控制點對單位圓上的外部控制點水平或垂直的的距離為 $4\left(\sqrt{2} -1\right)/3$ 時，分成四段的貝茲曲線，可以小於千分之一的最大半徑誤差近似於圓）。
位於固定偏移量的曲線（來自給定的貝茲曲線），又稱作偏移曲線（假平行於原來的曲線，如兩條鐵軌之間的偏移）無法以貝茲曲線精確的形成（某些瑣屑實例除外）。無論如何，現存的啟發法通常可為實際用途中給出近似值。

[編輯] 建構貝茲曲線

[編輯] 線性曲線

線性貝茲曲線演示動畫，t in [0,1]

線性貝茲曲線函數中的 t 會經過由 P₀ 至 P₁ 的 B(t) 所描述的曲線。例如當 t=0.25 時，B(t) 即一條由點 P₀ 至 P₁ 路徑的四分之一處。就像由 0 至 1 的連續 t，B(t) 描述一條由 P₀ 至 P₁ 的直線。

[編輯] 二次曲線

為建構二次貝茲曲線，可以中介點 Q₀ 和 Q₁ 作為由 0 至 1 的 t：

由 P₀ 至 P₁ 的連續點 Q₀，描述一條線性貝茲曲線。
由 P₁ 至 P₂ 的連續點 Q₁，描述一條線性貝茲曲線。
由 Q₀ 至 Q₁ 的連續點 B(t)，描述一條二次貝茲曲線。


二次貝茲曲線的結構		二次貝茲曲線演示動畫，t in [0,1]

[編輯] 高階曲線

為建構高階曲線，便需要相應更多的中介點。對於三次曲線，可由線性貝茲曲線描述的中介點 Q₀、Q₁、Q₂，和由二次曲線描述的點 R₀、R₁ 所建構：


三次貝茲曲線的結構		三次貝茲曲線演示動畫，t in [0,1]

對於四次曲線，可由線性貝茲曲線描述的中介點 Q₀、Q₁、Q₂、Q₃，由二次貝茲曲線描述的點 R₀、R₁、R₂，和由三次貝茲曲線描述的點 S₀、S₁ 所建構：


四次貝茲曲線的結構		四次貝茲曲線演示動畫，t in [0,1]

（還可參閱五階貝茲曲線的構成。）

[編輯] 應用

[編輯] 電腦繪圖

貝塞爾曲線被廣泛地在計算機圖形中用來為平滑曲線建立模型。

二次和三次貝塞爾曲線最為常見

[編輯] 程式範例

下列程式碼為一簡單的實際運用範例，展示如何使用 C 標出三次方貝茲曲線。注意，此處僅簡單的計算多項式係數，並讀盡一系列由 0 至 1 的 t 值；實踐中一般不會這麼做，遞歸求解通常會更快速——以更多的記憶體為代價，花費較少的處理器時間。不過直接的方法較易於理解並產生相同結果。以下程式碼已使運算更為清晰。實踐中的最佳化會先計算係數一次，並在實際計算曲線點的迴圈中反複使用。此處每次都會重新計算，損失了效率，但程式碼更清楚易讀。

曲線的計算可在曲線陣列上將相連點畫上直線——點越多，曲線越平滑。

在部分架構中，下以程式碼也可由動態程式設計進行最佳化。舉例來說，dt 是一個常數，cx * t 則等同於每次反覆就修改一次常數。經反覆應用這種最佳化後，迴圈可被重寫為沒有任何乘法（雖然這個過程不是穩定數值的）。

/*
產生三次方貝茲曲線的程式碼
*/
typedef struct
{
float x;
float y;
}
Point2D;
/*
cp 在此是四個元素的陣列:
cp[0] 為起始點，或上圖中的 P0
cp[1] 為第一個控制點，或上圖中的 P1
cp[2] 為第二個控制點，或上圖中的 P2
cp[3] 為結束點，或上圖中的 P3
t 為參數值，0 <= t <= 1
*/
Point2D PointOnCubicBezier( Point2D* cp, float t )
{
float   ax, bx, cx;
float   ay, by, cy;
float   tSquared, tCubed;
Point2D result;
/* 計算多項式係數 */
cx = 3.0 * (cp[1].x - cp[0].x);
bx = 3.0 * (cp[2].x - cp[1].x) - cx;
ax = cp[3].x - cp[0].x - cx - bx;
cy = 3.0 * (cp[1].y - cp[0].y);
by = 3.0 * (cp[2].y - cp[1].y) - cy;
ay = cp[3].y - cp[0].y - cy - by;
/* 計算位於參數值 t 的曲線點 */
tSquared = t * t;
tCubed = tSquared * t;
result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;
result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;
return result;
}
/*
ComputeBezier 以控制點 cp 所產生的曲線點，填入 Point2D 結構的陣列。
呼叫者必須分配足夠的記憶體以供輸出結果，其為 <sizeof(Point2D) numberOfPoints>
*/
void ComputeBezier( Point2D* cp, int numberOfPoints, Point2D* curve )
{
float   dt;
int	    i;
dt = 1.0 / ( numberOfPoints - 1 );
for( i = 0; i < numberOfPoints; i++)
curve[i] = PointOnCubicBezier( cp, i*dt );
}

另一種貝茲曲線的應用是在動畫中，描述物件的運動路徑等等。此處，曲線的 x、y 位置不用來標示曲線，但用來表示圖形位置。當用在這種形式時，連續點之間的距離會變的更為重要，且大多不是平均比例。點將會串的更緊密，控制點更接近每一個點，而更為稀疏的控制點會散的更開。如果需要線性運動速度，進一步處理時就需要循所需路徑將點平均分散。

[編輯] 有理貝茲曲線

有理貝茲增加可調節的權重，以提供更近似於隨意的形狀。分子是加權的伯恩斯坦形式貝茲曲線，而分母是加權的伯恩斯坦多項式的總和。

給定 n + 1 控制點 P_i，有理貝茲曲線可如下描述：

$\mathbf{B}(t) = \frac{ \sum_{i=0}^n b_{i,n}(t) \mathbf{P}_{i}w_i } { \sum_{i=0}^n b_{i,n}(t) w_i }$

或簡單的

$\mathbf{B}(t) = \frac{ \sum_{i=0}^n {n \choose i} t^i (1-t)^{n-i}\mathbf{P}_{i}w_i } { \sum_{i=0}^n {n \choose i} t^i (1-t)^{n-i}w_i }$

[編輯] 參閱

de Casteljau算法
樣條
貝茲樣條
貝茲曲面
貝茲三角
NURBS
string art，Bézier curves are also formed by many common forms of string art, where strings are looped across a frame of nails.
埃爾米特曲線

[編輯] 參考文獻

Paul Bourke: Bézier curves, http://astronomy.swin.edu.au/~pbourke/curves/bezier/
Donald Knuth: Metafont: the Program, Addison-Wesley 1986, pp. 123-131. Excellent discussion of implementation details; available for free as part of the TeX distribution.
Dr Thomas Sederberg, BYU Bézier curves, http://www.tsplines.com/resources/class_notes/Bezier_curves.pdf
J.D. Foley et al.: Computer Graphics: Principles and Practice in C (2nd ed., Addison Wesley, 1992)

posted on 2009-10-22 17:05 zmj 閱讀(5053) 評論(3) 編輯收藏引用

# re: 貝塞爾曲線 2014-02-13 11:00 xuthus