（一）世界坐標系向觀察坐標系的轉(zhuǎn)換

假如任何形體都放在世界坐標系中，那么計算是相當復(fù)雜的，為了簡化計算，我們需要把形體從世界坐標系轉(zhuǎn)到觀察坐標系中。觀察坐標系的原點在是世界坐標系的位置為Eye，Z軸與觀察方向一致（從Eye出發(fā)到At點的向量）如圖4-1所示：

                                                                            圖4-1

假設(shè)觀察坐標系的坐標軸分別以單位向量xaxis,yaxis,zaxis,則：

                                                               xaxis= normal (At-Eye);

                                                               yaxis= normal (cross(Up,zaxis));

                                                               zaxis= normal (zaxis,xaxis);

假設(shè)世界坐標系中任意一點P的坐標（x,y,z）,在觀察坐標系中的坐標（x'，y'，z'）。

x' = (P-Eye)* xaxis = x*xaxis.x + y* xaxis.y + z * xaxis.z - xaxis*Eye

y' = (P- Eye)*yaxis = x*yaxis.x + y* yaxis.y + z * yaxis.z - yaxis*Eye

z'= (P- Eye)*zaxis = x*zaxis.x + y* zaxis.y + z * zaxis.z - zaxis*Eye

                                    (x',y',z',1) = (x,y,z,1)*

所以從世界坐標系向觀察坐標系變換的矩陣為

（二）齊次裁剪透視投影變換

真實的物體是三維的，但是計算機屏幕是二維的，必須把三維物體投影到屏幕平面上，而且還要保存深度信息，這個變換過程稱為投影變換，如圖4-2所示

                                                                                                    圖4-2

假設(shè)視截體Y方向的張角fov，近平面Zn，遠平面的Zf，近平面的寬高比aspect，現(xiàn)在可以直到近平面的方程z=Zn，遠平面 z=Zf。

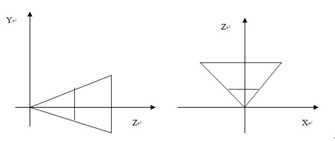
                                                                                                      圖4-3

由圖4-3可以看出，視截體的頂面方程為y=z*tan(fov/2);底面方程=-z*tan（fov/2）；視截體的右側(cè)面x=cot(fov/2)*aspect*z.

左側(cè)面方程x=-cot(fov/2)*aspect*z.

首先尋求把頂面y = z*tan(fov/2) 轉(zhuǎn)換為y'=1,y'=k*y ,k=cot(fov/2)*y/z就是滿足條件的變換，底面變換也是這個表達式。

右側(cè)面x = cot(fov/2)*aspect*z,轉(zhuǎn)換為x'=1, x'=p*x, 從而p=（tan(fov/2)/aspect)/z(左側(cè)面表達式相同).

最后尋求把近平面Zn轉(zhuǎn)換為z'=0;Zf轉(zhuǎn)換為z'=1.   z'= r*z + s.于是r* Zn + s =0,r*Zf + s =1,由此求出 r= /(Zf-Zn), s= -Zn/(Af-Zn).

透視投影變換矩陣=

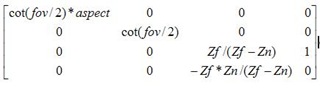
（三）視截體平面的計算

根據(jù)模型變換矩陣和投影變換矩陣，可以計算出視截體的6個平面。世界坐標系中的視截體在模型變換和透視投影變換后，成為觀察坐標系中的[-1,1]*[-1,1]*[0,1]。設(shè)模型變換A，投影變換B，M=A*B,視截體的方程:ax+by+cz+d=0。該平面在觀察坐標系中的形式為a'x'+b'y'+c'z'+d'=0.

(x',y',z',1) = (x,y,z,1)M

(x,y,z,1)(a,b,c,d)(轉(zhuǎn)置)=0

(x',y',z',1)(a',b',c',d')(轉(zhuǎn)置) = 0

可得：（x,y,z,1）M(a',b',c',d')(轉(zhuǎn)置) = 0

（a,b,c,d）(轉(zhuǎn)置)= M (a',b',c',d')（轉(zhuǎn)置）

a=M11a'+M12b'+M13c'+M14d'

b=M21a'+M22b'+M23c'+M24d'

c=M31a'+M32b'+M33c'+M34d'

d=M41a'+M42b'+M43c'+M44d'

視截體的6個平面的法向量均指向視截體內(nèi)部，視截體的左側(cè)面leftplane   觀察坐標系中的左側(cè)面x+1=0 ，代入上式可得視截體左側(cè)面的系數(shù)

a=M11+M14

b=M21+M24

c=M31+M34

d=M41+M44

右側(cè)面的方程1-x=0;系數(shù)

a=M14-M11

b=M24-M21

c=M34-M31

d=M44-M41

同理：頂面系數(shù)

a=M14-M12

b=M24-M22

c=M24-M32

d=M44-M42

底面系數(shù)

a=M12+M14

b=M22+M24

c=M32+M34

d=M42+M44

近平面系數(shù)：

a=M13

b=M23

c=M33

d=M43

遠平面系數(shù)：

a=M14-M13

b=M24-M23

c=M34-M33

d=M44-M43

上述內(nèi)容是涉及視截體計算的數(shù)學(xué)基礎(chǔ)，下一節(jié)實戰(zhàn)視截體編程！