Walking Curved Paths

In your game, the paths need not be so straight. You can have your objects move along a nice, curvy path, such as when a character walks around in a circle. Trying to define a smooth circular path using straight lines is nearly impossible, so you must develop a second type of path−one that can handle curves. Not just any type of curve, however. Remember that this is advanced animation−we're going for the big leagues here, and that major hitter you want is a cubic Bezier curve! As Figure 2.3 illustrates, a cubic Bezier curve uses four control points (two end points and two midpoints) to define the various aspects of the curve.

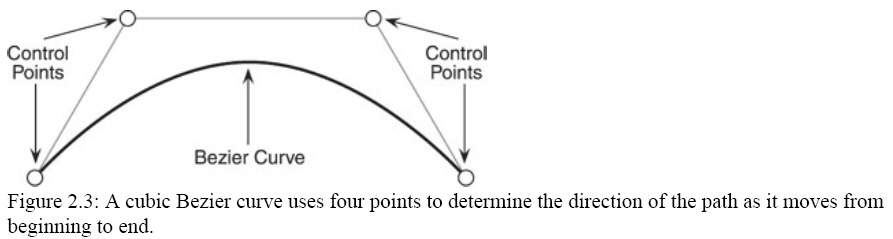
As you can see, a cubic Bezier curve is not a typical curve−it can bend and twist in a myriad of curved shapes. By manipulating the four control points you can create some really useful paths to use in your projects. The way a cubic Bezier curve works is fairly easy in theory, but a little difficult to implement.

To understand the theory behind a cubic Bezier curve, take a look at Figure 2.4, which shows how the curve is drawn using the four control points.

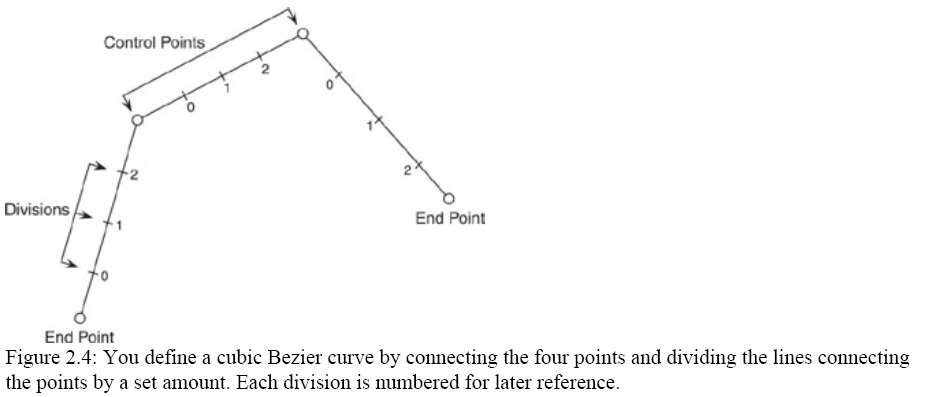
The purpose of dividing the lines that connect the curve's points is both for visual aid and to serve as the curve's granularity (or smoothness). The more additional divisions you add to each line, the smoother the resulting curve will look. To actually see the curve that the points create, you need to connect the divisions on either side of the line, as you can see in Figure 2.5

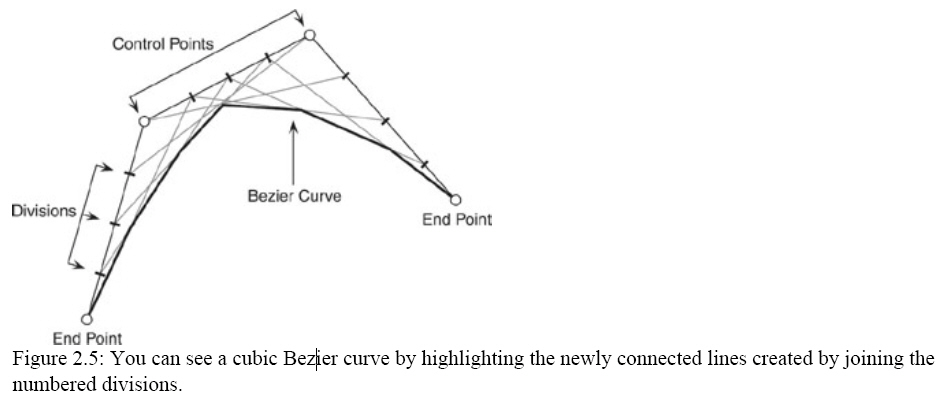
Although it's cool to draw the curve in the manner I just showed you, it won't make much sense to your computer, nor will it help you figure out the coordinates of a point in the curve. What you need to do is come up with a way to calculate the exact coordinates of any point along the curve. That way, you can do anything you want with the coordinates, from drawing curves to calculating the coordinates where you want to position an object along the curve path! The formula to calculate the coordinates along the curve is

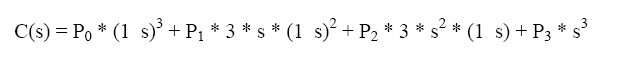
In the formula, the control points are defined as P0, P1, P2, and P3, which represent the starting point, first midpoint, second midpoint, and ending point, respectively. The resulting coordinates along the curve are defined as C(s), where s is a scalar value (or a time value) ranging from 0 to 1 that determines the position along the curve for which the coordinates should be calculated.

A value of s=0 designates the starting point, whereas a value of s=1 designates the ending point. Any value of s from 0 to 1 designates a point between the two end points. Therefore, to calculate the midpoint of the curve, you would specify s=0.5. The one−quarter position of the curve would be s=0.25, and so on.

To make things easy, you can create a function that takes the four control points (as vector objects) and a scalar value as parameters. The function will return another vector object that contains the coordinates of the point along the curve as specified by the four points and the scalar value. Call the function CubicBezierCurve, and use the following prototype to define it.

void CubicBezierCurve(D3DXVECTOR3 *vecPoint1, // Start point
  D3DXVECTOR3 *vecPoint2, // Midpoint 1
  D3DXVECTOR3 *vecPoint3, // Midpoint 2
  D3DXVECTOR3 *vecPoint4, // End point
  float Scalar,
  D3DXVECTOR3 *vecOut)
{

Now get ready for this−you're going to recreate the cubic Bezier curve formula in program code by replacing
the appropriate variables with the control point vectors and the scalar value.

// C(s) =
*vecOut =
// P0 * (1 − s)3 +
(*vecPoint1)*(1.0f−Scalar)*(1.0f−Scalar)*(1.0f−Scalar) +
// P1 * 3 * s * (1 − s)2 +
(*vecPoint2)*3.0f*Scalar*(1.0f−Scalar)*(1.0f−Scalar) +
// P2 * 3 * s2 * (1 − s) +
(*vecPoint3)*3.0f*Scalar*Scalar*(1.0f−Scalar) +
// P3 * s3
(*vecPoint4)*Scalar*Scalar*Scalar;
}

That's it! Yep, from now on you can calculate the coordinates along a cubic Bezier curve by passing the four control points' coordinates, a scalar, and a returning vector object. For example, going back to the sample curve, you can use the following function call to CubicBezierCurve to find the parametric midpoint:

D3DXVECTOR3 vecPos;

CubicBezierCurve(&D3DXVECTOR3(−50.0f, 25.0f, 0.0f),
  &D3DXVECTOR3(0.0f, 50.0f, 0.0f),
  &D3DXVECTOR3(50.0f, 0.0f, 0.0f),
  &D3DXVECTOR3(25.0f, −50.0f, 0.0f) ,
  0.5f, &vecPos);

Getting back to the point, you can use the return coordinates from the CubicBezierCurve function (contained in the vecPos vector object) as the coordinates in which to place an object in the game. By slowly changing the scalar value from 0 to 1 (over a specified amount of time), you move the object from the start of the path to the end. For instance, to travel a curved path over a period of 1,000 milliseconds, you can use the following code:

// vecPoints[4] = Starting, midpoint 1, midpoint 2, and end points
// Every frame, use the following code to position an object along the curve based on the current time.
D3DXVECTOR3 vecPos;
float Scalar = (float)(timeGetTime() % 1001) / 1000.0f;

CubicBezierCurve(&vecPoints[0], &vecPoints[1],  &vecPoints[2], &vecPoints[3],  Scalar, &vecPos);

// Use vecPos.x, vecPos.y, and vecPos.z coordinates for object

That's cool, but having to deal with a scalar value is a little unorthodox when you need to work with actual 3D unit measurements. I mean, how are you supposed to know which scalar value to use when you want to move an object 50 units along the curved path? Isn't there a way to calculate the length of the curve and use that, much like you did with straight lines?

Strangely enough, no. There is no easy way to calculate the length of a Bezier curve. However, you can approximate the length using a few simple calculations. Assuming the four control points of the curve are denoted as p0, p1, p2, and p3, you can add the lengths between the points p0 and p1, p1 and p2, and p2 and p3, divide the result in half, and add the length between points p0 and p3 (also divided in half). In code, those calculations would look like this:

// p[4] = four control points' coordinate vectors
float Length01 = D3DXVec3Length(&(p[1]−p[0]));
float Length12 = D3DXVec3Length(&(p[2]−p[1]));
float Length23 = D3DXVec3Length(&(p[3]−p[2]));
float Length03 = D3DXVec3Length(&(p[3]−p[0]));

float CurveLength = (Length01+Length12+Length23) * 0.5f + Length03 * 0.5f;

The CurveLength variable will therefore contain the estimated length of the curve. You'll use the CurveLength value much like you did in the straight−path calculations to convert the unit length to a scalar value to calculate the exact coordinates along the curve.

// Pos = position in curve (from 0−CurveLength)
float Scalar = Pos / CurveLength;
CubicBezierCurve(&vecPoints[0], &vecPoints[1], &vecPoints[2], &vecPoints[3],  Scalar, &vecPos);

As you can see, cubic Bezier curves aren't too difficult to use. The formulas are pretty basic, and I'd rather leave it up to the math textbooks to go into the details of the calculations (or a fine book like Kelly Dempski's Focus On Curves and Surfaces). For now, I'm only interested in making it work for your game project. Speaking of that, let's see what you can do with your newfound knowledge of using straight and curved paths to create routes.

Main Routine:

Runtime Snap:

download source file