我們能夠通過分別把兩個向量的各個分量相加得到向量之和,注意在相加之前必須保證它們有相同的維數。
u + v =
(ux+ vx,
uy+ vy,
uz+ vz)
圖5顯示的是幾何學上的向量相加。
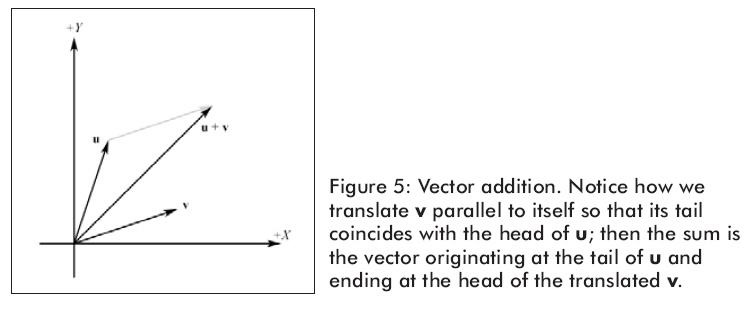
兩個向量相加的代碼,我們使用重載的加法操作符:
|
D3DXVECTOR3 u(2.0f, 0.0f,
1.0f);
D3DXVECTOR3 v(0.0f, -1.0f,
5.0f);
// (2.0 +
0.0, 0.0 + (-1.0), 1.0 + 5.0)
D3DXVECTOR3 sum = u + v;
// = (2.0f, -1.0f, 6.0f)
|
和加法類似,通過分別把兩個向量的各個分量相減得到向量之差。再次重聲兩個向量必須是相同維數。
u-v = u + (-v) = (ux
- vx, uy
- vy, uz -
vz)
圖6顯示的是幾何學上的向量相減。
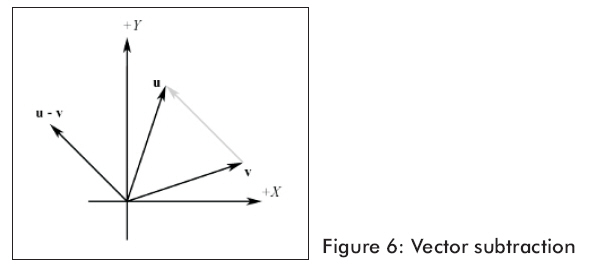
兩個向量相減的代碼,我們使用重載的減法操作符:
|
D3DXVECTOR3 u(2.0f, 0.0f,
1.0f);
D3DXVECTOR3 v(0.0f, -1.0f,
5.0f);
D3DXVECTOR3 difference = u
- v; // = (2.0f, 1.0f, -4.0f)
|
圖6顯示,向量減法得到一個從v向量終點到u向量終點的向量。假如我們解釋u和v的分量,我們能用向量相減找到從一個點到另一個點的向量。這是非常方便的操作,因為我們常常想找到從一個點到另一個點的方向向量。
我們能用一個標量與向量相乘,就象名字暗示的一樣,向量按比例變化。這種運算不會改變向量的方向,除非標量是負數,這種情況向量方向相反。