新建網(wǎng)頁 1
兩個AABB的相交性檢測
檢測兩個靜止AABB的相交性是很簡單的，只需要在每一維上單獨檢查它們的重合程度即可。如果在所有維上都沒有重合，那么這兩個AABB就不會相交。intersectAABBs()就是用這項技術(shù)來實現(xiàn)的。
//---------------------------------------------------------------------------
// Check if two AABBs intersect, and return true if so. Optionally return
// the AABB of their intersection if an intersection is detected.
//---------------------------------------------------------------------------
bool intersectAABBs(const AABB3& box1, const AABB3& box2, AABB3* boxIntersect)
{
// Check for no overlap
if (box1.min.x > box2.max.x) return false;
if (box1.max.x < box2.min.x) return false;
if (box1.min.y > box2.max.y) return false;
if (box1.max.y < box2.min.y) return false;
if (box1.min.z > box2.max.z) return false;
if (box1.max.z < box2.min.z) return false;
// We have overlap. Compute AABB of intersection, if they want it.
if (boxIntersect != NULL)
{
boxIntersect->min.x = max(box1.min.x, box2.min.x);
boxIntersect->max.x = min(box1.max.x, box2.max.x);
boxIntersect->min.y = max(box1.min.y, box2.min.y);
boxIntersect->max.y = min(box1.max.y, box2.max.y);
boxIntersect->min.z = max(box1.min.z, box2.min.z);
boxIntersect->max.z = min(box1.max.z, box2.max.z);
}
return true;
}
AABB間的動態(tài)測試稍微復(fù)雜一些。考慮一個由極值點
smin和smax定義的靜止AABB和一個由mmin和mmax定義的運動AABB。運動AABB的運動由向量d給出，t從0變換到1。
目標(biāo)是計算運動邊界框碰撞到靜止邊界框的時刻t（假設(shè)兩個邊界框剛開始時不相交）。要計算出t，我們需要計算出兩個邊界框在所有維上同時重合的第一個點。因為它的應(yīng)用范圍在2D或3D中，我們先在2D中解決它（擴(kuò)展到3D也是非常容易的）。先單獨分析每個坐標(biāo)，解決兩個(在3D中就是三個)獨立的一維問題，再把它們組合到一起就得到最終答案。
現(xiàn)在要解決的問題變成一維問題了。我們需要知道兩個矩形邊界框在特定維上重合的時間區(qū)間，假設(shè)把問題投影到x軸上，如圖13.15所示：
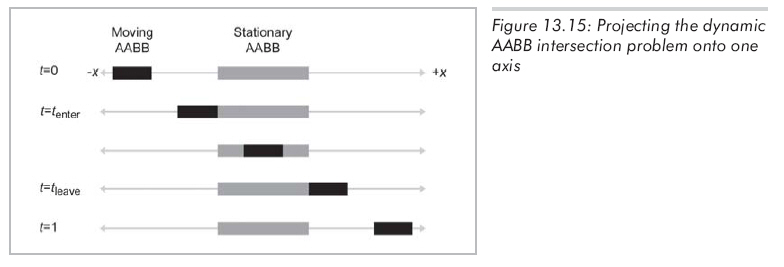
黑色矩形代表沿數(shù)軸滑動的運動AABB。當(dāng)圖13.15中的t=0時，運動的AABB完全位于靜止AABB的左邊，當(dāng)t=1時運動AABB完全位于靜止AABB右邊。tenter是兩個AABB開始相交時的時刻，tleave是兩個AABB脫離接觸的時刻。對于正在討論的維，設(shè)mmin(t)和mmax(t)代表運動AABB在時刻t的最小值和最大值：
mmin(t) = mmin(0) + td
mmax(t) = mmax(0) + td
mmin(0)和mmax(0)是運動AABB的起始位置，d是位移向量d在這個維上的分量。類似地用smin和smax來定義靜止AABB（當(dāng)然，它們和t是不相關(guān)的，因為這個AABB是靜止的）。tenter就是當(dāng)mmax(t)等于smin時的t值：
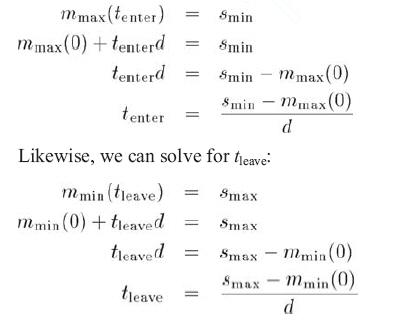
這里有三個要點：
（1）如果分母d為0，那么兩個矩形邊界框總是相交，或永不相交。
（2）如果運動AABB開始位于靜止AABB的右邊并向左移動，那么tenter將大于tleave。此時我們交換兩個值以確保tenter < tleave。
（3）tenter 和 tleave的值可能會超出[0, 1]這個區(qū)間，為了應(yīng)付t值超出區(qū)間的情況，可以認(rèn)為運動AABB是沿著平行于d的無限軌道移動。當(dāng)tenter> 1或tleave < 0時，在所討論的時間內(nèi)它們是不相交的，
現(xiàn)在我們已經(jīng)能夠求出兩個邊界框重合的時間范圍了，其邊界為tenter和tleave。在這段時間內(nèi)兩個邊界框會在某一維上相交，而所有維上的時間區(qū)間的交集就是兩個邊界框相交的時間段。圖13.16展示了在2D中的兩個時間區(qū)間（不要和圖13.15混淆，圖 13.16中的數(shù)軸是時間軸，而圖13.15中的數(shù)軸是x軸）。
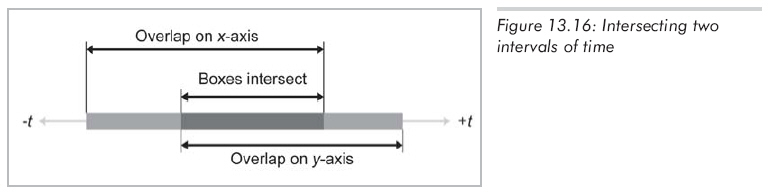
如果區(qū)間為空，那么兩個邊界框永遠(yuǎn)不會相交；如果區(qū)間范圍在[0, 1]之外，那么在所討論的時間段內(nèi)它們不相交。實際上，這個時間區(qū)間給出的信息比我們想要的多，因為我們只需要知道它們開始相交的時間點，而不需要知道結(jié)束相交的點。然而，我們?nèi)匀灰S持這個區(qū)間來檢測時間區(qū)間是否為空。
intersectMovingAABB()有上述過程的完整實現(xiàn)：
//---------------------------------------------------------------------------
// Return parametric point in time when a moving AABB collides
// with a stationary AABB. Returns > 1 if no intersection.
//---------------------------------------------------------------------------
float intersectMovingAABB(const AABB3& stationaryBox, const AABB3& movingBox, const Vector3& d)
{
// We'll return this huge number if no intersection
const float kNoIntersection = 1e30f;
// Initialize interval to contain all the time under consideration
float tEnter = 0.0f;
float tLeave = 1.0f;
// Compute interval of overlap on each dimension, and intersect this interval with the interval
// accumulated so far. As soon as an empty interval is detected, return a negative result
// (no intersection.) In each case, we have to be careful for an infinite of empty interval on
// each dimension.
// Check x-axis
if (d.x == 0.0f)
{
// Empty or infinite inverval on x
if ((stationaryBox.min.x >= movingBox.max.x) || (stationaryBox.max.x <= movingBox.min.x))
{
// Empty time interval, so no intersection.
return kNoIntersection;
}
// Inifinite time interval - no update necessary
}
else
{
float oneOverD = 1.0f / d.x; // Divide once
// Compute time value when they begin and end overlapping
float xEnter = (stationaryBox.min.x - movingBox.max.x) * oneOverD;
float xLeave = (stationaryBox.max.x - movingBox.min.x) * oneOverD;
// Check for interval out of order
if (xEnter > xLeave)
swap(xEnter, xLeave);
// Update interval
if (xEnter > tEnter) tEnter = xEnter;
if (xLeave < tLeave) tLeave = xLeave;
// Check if this resulted in empty interval
if (tEnter > tLeave)
return kNoIntersection;
}
// Check y-axis
if (d.y == 0.0f)
{
// Empty or infinite inverval on y
if ((stationaryBox.min.y >= movingBox.max.y) || (stationaryBox.max.y <= movingBox.min.y))
{
// Empty time interval, so no intersection
return kNoIntersection;
}
// Inifinite time interval - no update necessary
}
else
{
// Divide once
float oneOverD = 1.0f / d.y;
// Compute time value when they begin and end overlapping
float yEnter = (stationaryBox.min.y - movingBox.max.y) * oneOverD;
float yLeave = (stationaryBox.max.y - movingBox.min.y) * oneOverD;
// Check for interval out of order
if (yEnter > yLeave)
swap(yEnter, yLeave);
// Update interval
if (yEnter > tEnter) tEnter = yEnter;
if (yLeave < tLeave) tLeave = yLeave;
// Check if this resulted in empty interval
if (tEnter > tLeave)
return kNoIntersection;
}
// Check z-axis
if (d.z == 0.0f)
{
// Empty or infinite inverval on z
if ((stationaryBox.min.z >= movingBox.max.z) || (stationaryBox.max.z <= movingBox.min.z))
{
// Empty time interval, so no intersection
return kNoIntersection;
}
// Inifinite time interval - no update necessary
}
else
{
// Divide once
float oneOverD = 1.0f / d.z;
// Compute time value when they begin and end overlapping
float zEnter = (stationaryBox.min.z - movingBox.max.z) * oneOverD;
float zLeave = (stationaryBox.max.z - movingBox.min.z) * oneOverD;
// Check for interval out of order
if (zEnter > zLeave)
swap(zEnter, zLeave);
// Update interval
if (zEnter > tEnter) tEnter = zEnter;
if (zLeave < tLeave) tLeave = zLeave;
// Check if this resulted in empty interval
if (tEnter > tLeave)
return kNoIntersection;
}
// OK, we have an intersection.
// Return the parametric point in time where the intersection occurs.
return tEnter;
}
不幸的是，在實際情況中，物體的邊界框很少是軸對齊于同一個坐標(biāo)空間的。然而，因為這個檢測相對較快，所以可以把它當(dāng)作一個預(yù)備測試，可以先排除一些物體，然后再做一個特殊（通常計算量更大的）檢測。