HTML clipboard
HTML clipboard
四元數的對數、指數和標量乘運算
首先,讓我們重寫四元數的定義,引入一個新的變量α,等于半角θ/2:
α = θ/2
|| n || = 1
q = [cosα n sinα] = [cosα xsinα
ysinα zsinα]
q 的對數定義為公式10.15:
log q = log([cosα n sinα]) ≡ [0 α
n ]
公式10.15 四元數的對數
≡表示"恒等于",注意log q 的結果,它一般不是單位四元數。
指數以嚴格相反的方式定義,首先,設四元數 p 的形式為[0 α n ],
n 為單位向量:
p = [0 α n ] = [0 (αx αy αz)]
|| n || = 1
接著,指數定義為公式10.16:
exp p = exp([0 α n ]) = [cosα n
sinα]
公式10.16 四元數的指數
根據定義,exp p 總是返回單位四元數。
四元數的對數和指數類似于它們的標量形式,回憶一下,對于標量α,有下列關系成立:

同樣,四元數指數運算為四元數對數運算的逆運算:
exp(log q ) = q
最后,四元數能與一個標量相乘。其計算方法非常直接:每個分量都乘以這個標量,給定標量k和四元數 q ,有公式 10.17:
k q = k[w v ] = [kw k v
] = k[w (x y z)] = [kw kx ky kz]
公式10.17 四元數和標量相乘
一般不會得到單位四元數,這也是為什么在表達角位移的場合中標量乘不是那么有用的原因。
四元數求冪
四元數能作為底數,記作 qt
(不要和指數運算混淆,指數運算只接受一個四元數作為參數,而四元數求冪有兩個參數 ---- 四元數和指數)。四元數求冪的意義類似于實數求冪。回憶一下,a0
= 1, a1 = a,a為非零標量。當t從0變到1時,at從1到a。四元數求冪有類似的結論:當t從0變到1,
qt從[1, 0 ]到 q 。
這對四元數求冪非常有用,因為它可以從角位移中抽取"一部分"。例如,四元數 q
代表一個角位移,現在想要得到代表1/3這個角位移的四元數,可以這樣計算: q1/3。
指數超出[0, 1]范圍外的幾何行為和預期的一樣(但有一個重要的注意事項)。例如, q2代表的角位移是
q 的兩倍。假設 q 代表繞x軸順時針旋轉30度,那么 q2代表繞x軸順時針旋轉60度,
q-1/3代表繞x軸逆時針旋轉10度。
上面提到的注意事項是,四元數表達角位移時使用最短圓弧,不能"繞圈"。繼續上面的例子, q4不是預期的繞x軸順時針旋轉240度,而是逆時針80度。顯然,向一個方向旋轉240度等價于向相反的方向旋轉80度,都能得到正確的"最終結果"。但是,在此基礎上的進一步運算,產生的就可能不是預期的結果了。例如,(q4)1/2不是 q 2,盡管我們感覺應該是這樣。一般來說,凡是涉及到指數運算的代數公式,如(as)t
= a(st),對四元數都不適用。
現在,我們已經理解四元數求冪可以為我們做什么了。讓我們看看它的數學定義,四元數求冪定義在前一節討論的"有用"運算上,定義如公式10.18:

注意,對于標量求冪,也有類似結論:

不難理解為什么當t從0變到1時 q'從單位四元數變到 q
。注意到對數運算只是提取了軸 n
和角度θ;接著,和指數t進行標量乘時,結果是θ乘以t;最后,指數運算"撤銷"了對數運算,從tθ和 n 重新計算w和
v 。上面給出的定義就是標準數學定義,在理論上非常完美,但直接轉換到代碼卻是很復雜的。程序清單10.1所示的代碼展示了怎樣計算
q'的值。
Listing 10.1: Code to raise a quaternion to a power
// Quaternion (input and output)
float w,x,y,z;
// Input exponent
float exponent;
// Check for the case of an identity quaternion.
// This will protect against divide by zero
if (fabs(w) < .9999f)
{
// Extract the half angle alpha (alpha = theta/2)
float alpha = acos(w);
// Compute new alpha value
float newAlpha = alpha * exponent;
// Compute new w value
w = cos(newAlpha);
// Compute new xyz values
float mult = sin(newAlpha) / sin(alpha);
x *= mult;
y *= mult;
z *= mult;
}
關于這些代碼,需要注意的地方有:
(1)有必要做單位四元數的檢查。因為w=+(-)1會導致mult的計算中出現除零現象。單位四元數的任意次方還是單位四元數。因此,如果檢測到輸入是單位四元數,忽略指數直接返回原四元數即可。
(2)計算alpha時,使用了acos函數,它的返回值是正的角度。這并不會違背一般性,任何四元數都能解釋成有正方向的旋轉角度,因為繞某軸的負旋轉等價于繞指向相反方向的軸的正旋轉。
四元數插值 ---- "slerp"
當今3D數學中四元數存在的理由是由于一種稱作slerp的運算,它是球面線性插值的縮寫(Spherical Linear
Interpolation)。slerp運算非常有用,因為它可以在兩個四元數間平滑插值。slerp運算避免了歐拉角插值的所有問題。
slerp是一種三元運算,這意味著它有三個操作數。前兩個操作數是兩個四元數,將在它們中間插值。設這兩個"開始"和"結束"四元數分別為 q 0和
q 1。插值參數設為變量t,t在0到1之間變化,slerp函數:slerp( q 0,
q 1, t),將返回 q 0到 q 1之間的插值方位。
能否利用現有的數學工具推導出slerp公式呢?如果是在兩個標量a0和a1間插值,我們會使用下面的標準線性插值公式:
Δa = a1 - a0
lerp(a0, a1, t) = a0 + tΔa
標準線性插值公式從a0開始,并加上a0和a1差的t倍,有三個基本步驟:
(1)計算兩個值的差。
(2)取得差的一部分。
(3)在初始值上加上差的一部分。
可以使用同樣的步驟在四元數間插值:
(1)計算兩個值的差, q 0到 q 1的角位移由Δ q
= q 0-1 q 1給出。
(2)計算差的一部分,四元數求冪可以做到,差的一部分由(Δ q )t給出。
(3)在開始值上加上差的一部分,方法是用四元數乘法來組合角位移: q 0(Δ q )t
這樣,得到slerp的公式如公式10.19所示:

這是理論上的slerp計算過程,實踐中,將使用一種更加有效的方法。
我們在4D空間中解釋四元數,因為所有我們感興趣的四元數都是單位四元數,所以它們都"存在"于一個 4D"球面"上。
slerp的基本思想是沿著4D球面上連接兩個四元數的弧插值(這就是球面線性插值這個名稱的由來)。
可以把這種思想表現在平面上,設兩個2D向量 v 0和 v 1,都是單位向量。我們要計算
v 1,它是沿 v 0到 v 1弧的平滑插值。設w是
v 0到 v 1弧所截的角,那么 v t就是繞
v 1沿弧旋轉tw的結果,如圖10.10所示:

將 v t表達成 v 0和 v 1的線性組合,從另一方面說,存在兩個非零常數k0和k1,使得:
v t = k0 v 0
+ k1 v 1
可以用基本幾何學求出k0和k1,圖10.11展示了計算的方法:
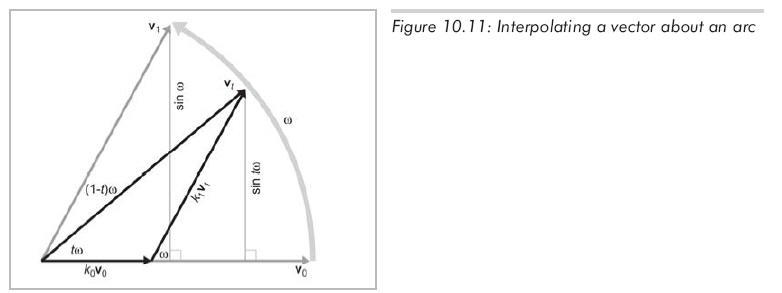
對以k1 v 1為斜邊的直角三角形應用三角公式得:

這里有兩點需要考慮。第一,四元數 q 和- q
代表相同的方位,但它們作為slerp的參數時可能導致不一樣的結果,這是因為4D球面不是歐式空間的直接擴展。而這種現象在2D和3D中不會發生。解決方法是選擇
q 0和 q 1的符號使得點乘 q 0 . q
1的結果是非負。第二個要考慮的是如果 q 0和 q
1非常接近,sinθ會非常小,這時除法可能會出現問題。為了避免這樣的問題,當sinθ非常小時使用簡單的線性插值。程序清單10.2把所有的建議都應用到了計算四元數的slerp中:
Listing 10.2: How slerp is computed in practice
// The two input quaternions
float w0,x0,y0,z0;
float w1,x1,y1,z1;
// The interpolation parameter
float t;
// The output quaternion will be computed here
float w,x,y,z;
// Compute the "cosine of the angle" between the
// quaternions, using the dot product
float cosOmega = w0*w1 + x0*x1 + y0*y1 + z0*z1;
// If negative dot, negate one of the input
// quaternions to take the shorter 4D "arc"
if (cosOmega < 0.0f) {
w1 = –w1;
x1 = –x1;
y1 = –y1;
z1 = –z1;
cosOmega = –cosOmega;
}
// Check if they are very close together to protect
// against divide-by-zero
float k0, k1;
if (cosOmega > 0.9999f) {
// Very close - just use linear interpolation
k0 = 1.0f–t;
k1 = t;
} else {
// Compute the sin of the angle using the
// trig identity sin^2(omega) + cos^2(omega) = 1
float sinOmega = sqrt(1.0f – cosOmega*cosOmega);
// Compute the angle from its sin and cosine
float omega = atan2(sinOmega, cosOmega);
// Compute inverse of denominator, so we only have
// to divide once
float oneOverSinOmega = 1.0f / sinOmega;
// Compute interpolation parameters
k0 = sin((1.0f – t) * omega) * oneOverSinOmega;
k1 = sin(t * omega) * oneOverSinOmega;
}
// Interpolate
w = w0*k0 + w1*k1;
x = x0*k0 + x1*k1;
y = y0*k0 + y1*k1;
z = z0*k0 + z1*k1;