新建網頁 1
在3D中,平面是到兩個點的距離相等的點的集合。平面完全是平的,沒有厚度,且無限延伸。
平面方程 ---- 隱式定義
可以用類似于定義直線的方法來定義平面,平面的隱式定義由所有滿足平面方程的點p=(x, y, z)給出,平面方程的兩種記法如公式12.11所示:
ax + by + cz = d
p . n = d
公式12.11 平面方程
注意第二種形式中,n = [a, b, c]。一旦知道n,就能用任意已知的平面上的點來計算d。
向量n也稱作平面的法向量,因為它垂直于平面。讓我們來驗證它,設p和q都在平面上,滿足平面方程。將p、q代入式12.11,即有:

最后一行點乘的幾何意義就是n垂直于從q到p的向量,這對于平面上的任意p、q點都是成立的,因此n垂直于平面上的任意向量。
我們還假設平面有"正面"和"反面"。一般來說,n指向的方向是平面的正面(front side)。即從n的頭向尾看,我們看見的是正面,如圖12.13所示:

將n限制為單位長度并不會失去一般性,而且通常會給計算帶來方便。
用三個點定義
另一種定義平面的方法是給出平面上不共線的三個點,也就是說,這三個點不在一條直線上。(如果三個點在一條直線上,就存在無數多個平面包含這條直線,這樣也就無法說明我們指的是哪個平面了。)
讓我們通過平面上的三個點p1、p2和p3來計算n和d。先計算n,n指向什么方向呢?左手坐標系中的慣例是:當從平面的正面看時,p1、p2和p3以順時針方向列出。(右手坐標系中,經常假設這些點以逆時針方向列出,這樣不管使用哪種坐標系公式,結果都是相同的。)
圖12.14展示了使用平面上的三個點計算平面的法線向量的情況。
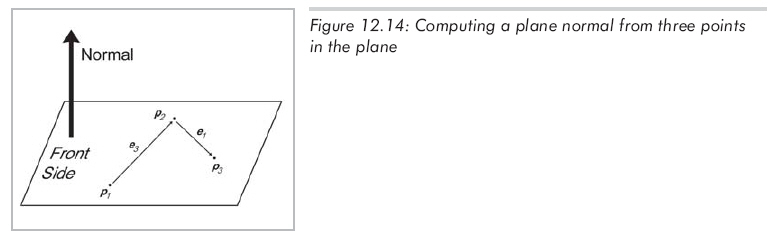
我們按順時針方向構造兩個向量(如圖12.14所示),"e"代表"邊(edge)"向量,因為這個公式經常用來計算三角形代表的平面。這兩個向量叉乘的結果就是n,但可能不是單位向量,但我們可以單位化n,以上所有過程用公式12.12來簡介地概括:
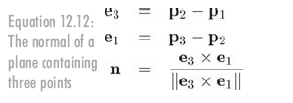
注意,如果這些點共線,則e3與e1平行。這樣叉乘為0,不能單位化。這個數學上的特例與物理特例相吻合:共線點不能唯一地定義一個平面。
現在知道了n,剩下的就是求d,可以由某個點與n點乘獲得。
多于三個點的"最佳"平面
有時,我們希望從一組三個以上的點集求出平面方程,這種點集最常見的例子就是多邊形頂點。在這種情況下,這些頂點繞多邊形順指針地列出。(順序很重要,因為要依據它決定哪邊是"正面"哪邊是"反面"。)
一種糟糕的方式是任選三個連續的點并用這三個點計算平面方程。畢竟所選的三個點可能共線,或接近共線。因為數值精度的問題,這將非常糟糕。或者,多邊形可能是凹的,所選的點恰好在凹處,從而構成了逆時針(將導致法向量方向錯誤)。又或者,多邊形上的頂點可能不是共面的,這可能是由數值上的不精確,或錯誤的生成多邊形的方法所引起的。我們真正想要的是從點集中求出"最佳"平面的方法,該平面綜合考慮了所有的點。設給定n個點:

如果我們限制n必須為單位向量,則這個向量必須單位化。
求和符號能使公式12.13更簡潔些,設pn+1 = p1,則有:

如下代碼展示了怎樣從點集中求出最佳法向量:
Listing 12.2: Computing the best-fit plane normal for a set of points
Vector3 computeBestFitNormal(const Vector3 v[], int n)
{
// Zero out sum
Vector3 result = kZeroVector;
// Start with the "previous" vertex as the last one.
// This avoids an if-statement in the loop
const Vector3 *p = &v[n–1];
// Iterate through the vertices
for (int i = 0 ; i < n ; ++i)
{
// Get shortcut to the "current" vertex
const Vector3 *c = &v[i];
// Add in edge vector products appropriately
result.x += (p–>z + c–>z) * (p–>y – c–>y);
result.y += (p–>x + c–>x) * (p–>z – c–>z);
result.z += (p–>y + c–>y) * (p–>x – c–>x);
// Next vertex, please
p = c;
}
// Normalize the result and return it
result.normalize();
return result;
}
最佳d值為每個點對應的d的平均值:

點到平面的距離
設想一個平面和一個不在平面上的點q,平面上存在一個點p,它到q的距離最短。很明顯,從p到q的向量垂直于平面,且形式為an。如圖12.15所示:

假設n為單位向量,那么p到q的距離(也就是q到平面的距離)就是a了。(如果q在平面的反面,這個距離為負。)令人驚奇的是,不用知道p的位置就能計算出a。讓我們回顧q的原定義,并做一些向量計算以消掉p,如公式12.14所示: