包含平移的線性變換稱(chēng)作仿射變換,3D中的仿射變換不能用 3 x 3 矩陣表達(dá),必須使用4
x 4矩陣。
一般來(lái)說(shuō),變換物體相當(dāng)于以相反的量變換描述這個(gè)物體的坐標(biāo)系。當(dāng)有多個(gè)變換時(shí),則需要以相反的順序變換相反的量。例如,將物體順時(shí)針旋轉(zhuǎn)20度,擴(kuò)大200%,等價(jià)于將坐標(biāo)系縮小200%,再逆時(shí)針旋轉(zhuǎn)20度。
2D中的旋轉(zhuǎn)
在2D環(huán)境中,物體只能繞某個(gè)點(diǎn)旋轉(zhuǎn),因?yàn)楝F(xiàn)在暫不考慮平移。這里我們進(jìn)一步限制物體,使其只繞原點(diǎn)旋轉(zhuǎn)。2D中繞原點(diǎn)的旋轉(zhuǎn)只有一個(gè)參數(shù),角度θ,它描述了旋轉(zhuǎn)量。逆時(shí)針旋轉(zhuǎn)經(jīng)常(不是必須)被認(rèn)為是正方向,順時(shí)針?lè)较蚴秦?fù)方向。圖8.5展示了基向量p,q繞原點(diǎn)旋轉(zhuǎn),得到新的基向量p',q'。
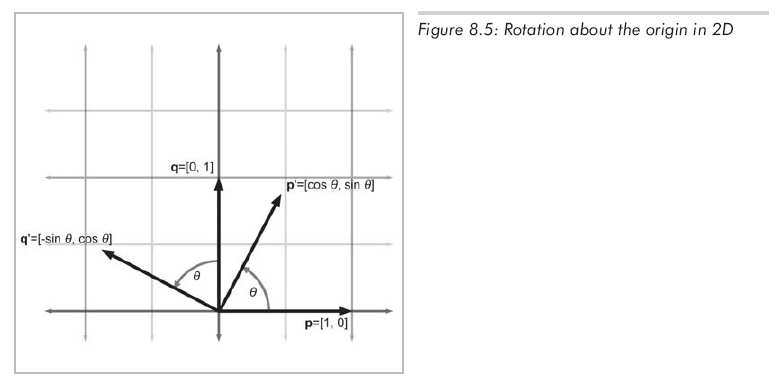
現(xiàn)在我們知道了旋轉(zhuǎn)后基向量的值,就可以以公式8.1的形式構(gòu)造矩陣如下:
3D中繞坐標(biāo)軸的旋轉(zhuǎn)
在3D場(chǎng)景中,繞軸旋轉(zhuǎn)而不是點(diǎn)(此時(shí)軸指的是旋轉(zhuǎn)所繞的直線,不一定是笛卡爾坐標(biāo)軸x,y,z)。再次聲明,這里暫不考慮平移,所以只討論旋轉(zhuǎn)軸穿過(guò)原點(diǎn)的情況。
繞軸旋轉(zhuǎn)角度θ時(shí),必須知道哪個(gè)方向被認(rèn)為“正”,哪個(gè)方向被認(rèn)為“負(fù)”,左手坐標(biāo)系中定義此方向的規(guī)則為左手法則。首先,要明確旋轉(zhuǎn)軸指向哪個(gè)方向。當(dāng)然,旋轉(zhuǎn)軸在理論上是無(wú)限延伸的,但我們還是要認(rèn)為它有正端點(diǎn)和負(fù)端點(diǎn)。與笛卡爾坐標(biāo)軸定義坐標(biāo)系相同,左手法則是這樣的:伸出左手,大拇指向上,其余手指彎曲。大拇指指向旋轉(zhuǎn)軸的正方向,此時(shí),四指彎曲的方向就是旋轉(zhuǎn)的正方向。如圖8.6所示。
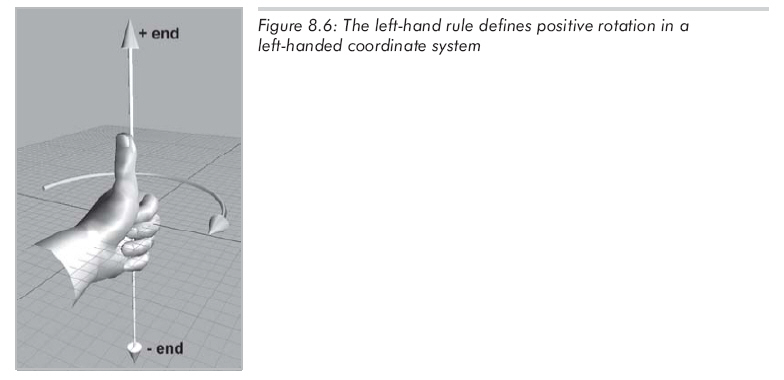
如果用的是右手坐標(biāo)系,也有類(lèi)似的法則,不過(guò)是用右手代替左手,如圖8.7所示:
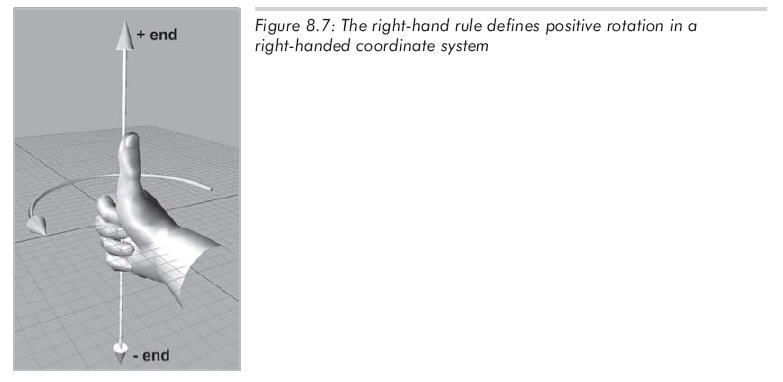
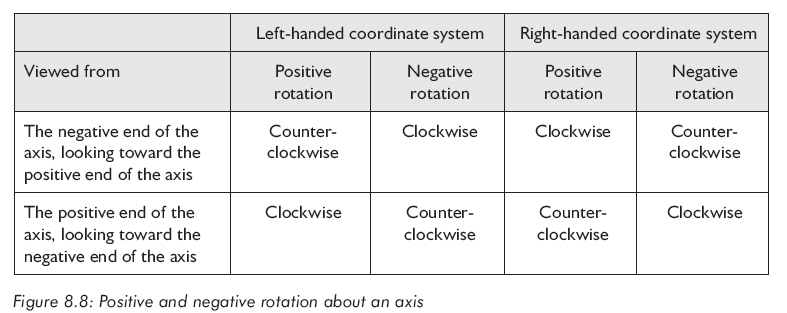
圖8.8顯示了另一種正方向的定義:
最為常見(jiàn)的旋轉(zhuǎn)是繞某坐標(biāo)軸的簡(jiǎn)單旋轉(zhuǎn),讓我們從繞x軸旋轉(zhuǎn)開(kāi)始,如圖8.9所示:

求出旋轉(zhuǎn)后的基向量,可以得到矩陣,見(jiàn)公式8.2。
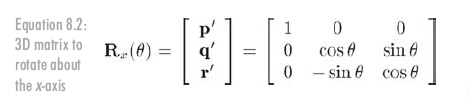
Rotation about the y-axis is similar:
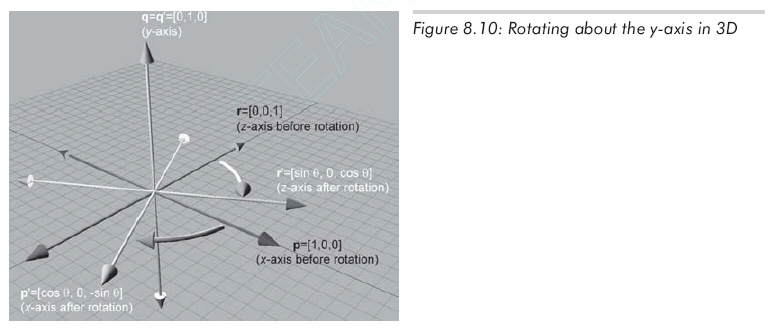
The matrix to rotate about the y-axis:
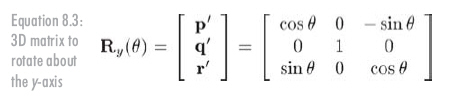
Finally, rotating about the z-axis:
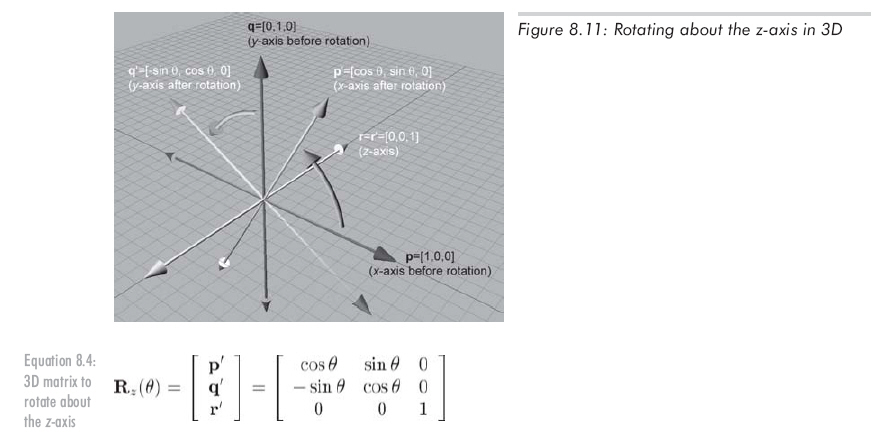
3D中繞任意軸的旋轉(zhuǎn)
當(dāng)然也能繞3D中的任意軸旋轉(zhuǎn)。因?yàn)檫@里不考慮平移,可以假設(shè)旋轉(zhuǎn)軸通過(guò)原點(diǎn),這種旋轉(zhuǎn)比繞坐標(biāo)軸的旋轉(zhuǎn)更復(fù)雜也更少見(jiàn)。用單位向量n描述旋轉(zhuǎn)軸,和前面一樣用θ描述旋轉(zhuǎn)量。
讓我們導(dǎo)出繞軸n旋轉(zhuǎn)角度θ的矩陣,也就是說(shuō),我們想得到滿足下面條件的矩陣 R(n,
θ):
vR(n, θ) = v'
v'是向量v繞軸n旋轉(zhuǎn)后的向量。讓我們看看能否用v,n和θ表示v'。我們的想法是在垂直于n的平面中解決這個(gè)問(wèn)題,那么這就轉(zhuǎn)換為了一個(gè)簡(jiǎn)單的2D問(wèn)題。為了做到這一點(diǎn),將v分解為兩個(gè)分量:v||和v⊥,分別平行于n和垂直于n,并有v
= v|| + v⊥。因?yàn)?strong>v||平行于n,所以繞n旋轉(zhuǎn)不會(huì)影響它。故只要計(jì)算出v⊥繞n旋轉(zhuǎn)后的
v⊥',就能得到 v' =v||
+ v⊥'。為了計(jì)算v⊥',我們構(gòu)造向量v||
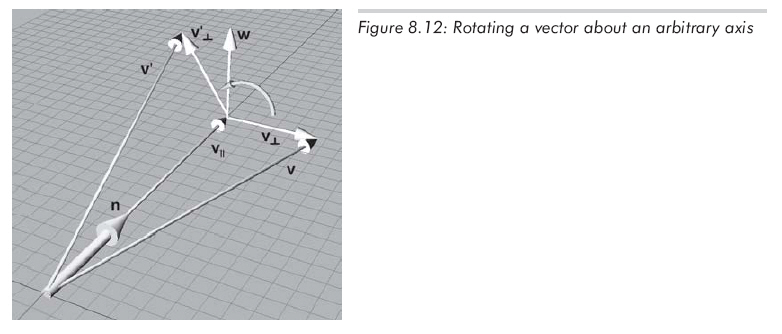
,v⊥和臨時(shí)向量w,如圖8.12所示:
 ’
’
上圖展示了以下向量:
(1)v|| 是v平行于n的分量,另一種說(shuō)法就是v||
是v在n上的投影,用(v.n)n計(jì)算。
(2)v⊥是v垂直于n的分量,因?yàn)?
v = v|| + v⊥,所以
v⊥ = v - v||。v⊥是v投影到垂直于n的平面上的結(jié)果。
(3)w是同時(shí)垂直于v||和v⊥的向量,它的長(zhǎng)度和v⊥的相同。w和v⊥同在垂直于n的平面中,w是v⊥繞n旋轉(zhuǎn)90度的結(jié)果,由n
x v⊥可以得到。
現(xiàn)在,v'垂直于n的分量可以表示為:


