Points Within
Time Limit: 2 Seconds Memory Limit: 65536 KB
Statement of the Problem
Several drawing applications allow us to draw polygons and almost all of them allow us to fill them with some color. The task of filling a polygon reduces to knowing which points are inside it, so programmers have to colour only those points.
You're expected to write a program which tells us if a given point lies inside a given polygon described by the coordinates of its vertices. You can assume that if a point is in the border of the polygon, then it is in fact inside the polygon.
Input Format
The input file may contain several instances of the problem. Each instance consists of: (i) one line containing integers N, 0 < N < 100 and M, respectively the number of vertices of the polygon and the number of points to be tested. (ii) N lines, each containing a pair of integers describing the coordinates of the polygon's vertices; (iii) M lines, each containing a pair of integer coordinates of the points which will be tested for "withinness" in the polygon.
You may assume that: the vertices are all distinct; consecutive vertices in the input are adjacent in the polygon; the last vertex is adjacent to the first one; and the resulting polygon is simple, that is, every vertex is incident with exactly two edges and two edges only intersect at their common endpoint. The last instance is followed by a line with a 0 (zero).
Output Format
For the ith instance in the input, you have to write one line in the output with the phrase "Problem i:", followed by several lines, one for each point tested, in the order they appear in the input. Each of these lines should read "Within" or "Outside", depending on the outcome of the test. The output of two consecutive instances should be separated by a blank line.
Sample Input
3 1
0 0
0 5
5 0
10 2
3 2
4 4
3 1
1 2
1 3
2 2
0
Sample Output
Problem 1:
Outside
Problem 2:
Outside
Within
#include <stdio.h>
#include <math.h>
double D,M,A,J,jtime, jtimeaccellimit, jtimespeedlimit, jtimedistlimit,
atime, dist, delta, a, b, c, r;
double cubrt(double x) {
return (exp(log(x)/3));
}
main(){
while (4 == scanf("%lf%lf%lf%lf",&D,&M,&A,&J)) {
jtimeaccellimit = A/J;
jtimespeedlimit = sqrt(M/J);
jtimedistlimit = cubrt(D/2/J);
jtime = jtimeaccellimit;
if (jtimespeedlimit < jtime) jtime = jtimespeedlimit;
if (jtimedistlimit < jtime) jtime = jtimedistlimit;
atime = (M - J*pow(jtime,2))/A;
a = 0.5*A;
b = A*jtime + 0.5*J*pow(jtime,2);
c = J * pow(jtime,3) - D/2;
r = (-b + sqrt(b*b - 4*a*c))/2/a;
if (r < atime) atime = r;
dist = J * pow(jtime,3)
+ 0.5*J*pow(jtime,2)*atime + 0.5*A * pow(atime,2)
+ A * atime*jtime;
printf("%0.1lf\n",4*jtime+2*atime+2*(D/2-dist)/M);
}
}
文章來源: http://www.cnblogs.com/kuangbin/archive/2011/11/15/2250031.html
Probability
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2313 Accepted Submission(s): 1146
Problem Description
Mickey is interested in probability recently. One day , he played a game which is about probability with mini.First mickey gives a letter and a word to mini.Then mini calculate the probability that the letter appears in the word.For example,give you the letter "a" and the word "apple". the probability of this case is 0.20000.
Input
The input contains several test cases. Each test case consists of a letter and a word.The length of the word is no longer than 200.
Output
For each test case, print the probability rounded to five digits after the decimal point.
Sample Input
Sample Output
Author
KiKi
Source
Recommend
威士忌
#include<stdio.h>
#include<string.h>
char str[210];
int main()
{
char ch1,ch2;
while(scanf("%c %s",&ch1,&str)!=EOF)
{
if(ch1>='a'&&ch1<='z')ch2=ch1-'a'+'A';
else ch2=ch1-'A'+'a';
int len=strlen(str);
int tt=0;
for(int i=0;i<len;i++)
{
if(str[i]==ch1||str[i]==ch2)tt++;
}
printf("%.5lf\n",(double)tt/len);
getchar();
}
return 0;
}
文章來源: http://www.cnblogs.com/kuangbin/archive/2011/11/15/2249142.html
/*
題意:就是給你一個有2^n個輸入的門電路,初始輸入為全0,問至少要改變輸入
開關多少次(即改變輸入中0、1多少次)才能得到所需的0、1輸出序列。
題意分析:
這道題的數據范圍為k<10000,所以不能枚舉暴搞,只能用遞推來求解。
仔細分析就可一發現當有多個0或多個1在一起時,是不用改變開關的。只有
在輸出序列中出現0到1或1到0的跳變時才需要改變開關。
*/
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int ch[10010];
char str[10010];
int n;
int solve(int i)//遞歸求從0變1需要的至少次數
{
if(2*i+1>=n-1)
{
if(ch[i]==0)return 1;
else return 2;
}
if(ch[i]==1) return solve(2*i+1)+solve(2*i+2);
else return min(solve(2*i+1),solve(2*i+2));
}
int main()
{
freopen("test.in","r",stdin);
freopen("test.out","w",stdout);
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
scanf("%s",&str);
for(int i=0;i<n-1;i++)
{
scanf("%d",&ch[i]);
}
int m=solve(0);
//printf("%d\n",m);
int res;
if(str[0]=='0') res=0;
else res=1;
int len=strlen(str);
for(int i=1;i<len;i++)//找變化的次數,1變0,0變1
{
if(str[i]!=str[i-1])res++;
}
if(res)res+=m-1;//加上第一次變1 的次數,以后改變只需要一次就好了
printf("%d\n",res);
}
return 0;
}
1A,好爽,去福州前去刷刷水題很痛快。。。。期待福州拿牌回來。。。
Sheryl's Circuit I
| Time Limit: 1000MS |
|
Memory Limit: 65536K |
| Total Submissions: 1037 |
|
Accepted: 430 |
Description
In the Design of Digital Logic class, Sheryl is asked to design a device which can produce a digital signal (a sequence of 0 and 1), given by the professor. After several sleepless nights, she completes a kind of Boolean circuit which looks like a complete binary tree as showed in Figure 1. Every node of the tree is a Boolean arithmetic unit (BAU) which takes in inputs from its both children and produce an output to its parent. The inputs of BAU are either 1 or 0, and the output should be calculated due to the type of BAU which is either ∧ or ∨. The truth tables of the two types are also showed in Figure 1. The INPUT of Sheryl's circuit is the sequence of inputs of the lowest-level BAUs and the OUTPUT is the output of the top BAU.
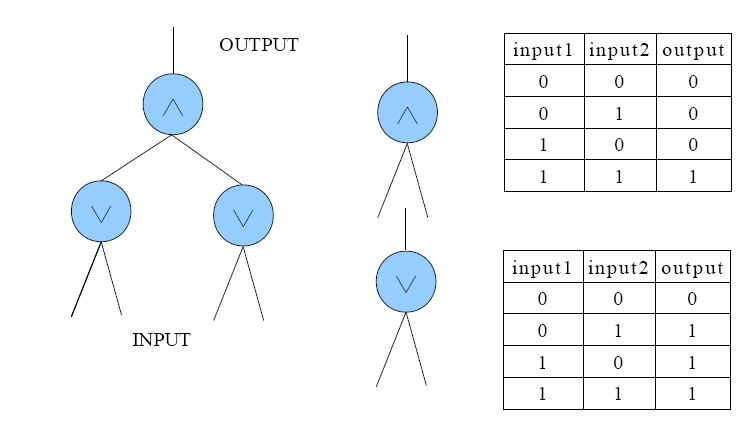
Figure 1
To accomplish the assignment, Sheryl has to manually handle the INPUT to produce the expected signal. For example, assuming Sheryl's circuit is the one showed in Figure 1, when the professor wants (0, 0, 0, 1, 1, 1) as the signal, the INPUT may alter as this: (0, 0, 0, 0) -> (0, 0, 1, 1) -> (1, 1, 0, 0) -> (1, 1, 1, 1) -> (1, 0, 1, 0) -> (0, 1, 0, 1). But this is too complex because Sheryl has to change the INPUT 14(2 + 4 + 2 + 2 + 4) times totally! So a more clever way is preferable, say (0, 0, 0, 0) -> (0, 0, 0, 0) -> (0, 0, 0, 0) -> (0, 1, 0, 1) -> (0, 1, 0, 1) -> (0, 1, 0, 1), which requires only 2(0 + 0 + 2 + 0 +0) changes of the INPUT.
Given Sheryl's circuit and the signal expected, your task is to find the minimal changes of the INPUT to produce the signal. Note the INPUT begins with all 0s.
Input
There are multiple test cases.
The first line contains the number of test cases.
Each test case begins with an integer N( ≤ 10000), the number of inputs of Sheryl's circuit. It is guaranteed that N equals 2k, where k is an integer.
The next line contains the expected signal which consists of 0 and 1 only. The length of the signal is no more than 10000.
Next N - 1 numbers describe the types of the BAUs, 0 for ∨ and 1 for ∧. The describing order is from top level to bottom level. For the same level it is from left to right.
Output
For each test case output the minimal number of changes in a separate line.
Sample Input
2
4
010101
0 0 0
4
111111
1 1 1
Sample Output
5
4
Source
題意:就是給你一個有2^n個輸入的門電路,初始輸入為全0,問至少要改變輸入開關多少次(即改變輸入中0、1多少次)才能得到所需的0、1輸出序列。
題意分析:
這道題的數據范圍為k<10000,所以不能枚舉暴搞,只能用遞推來求解。
仔細分析就可一發現當有多個0或多個1在一起時,是不用改變開關的。只有在輸出序列中出現0到1或1到0的跳變時才需要改變開關。
文章來源: http://www.cnblogs.com/kuangbin/archive/2011/11/14/2248770.html
Problem 1021 飛船賽
Accept: 1368 Submit: 5167
Time Limit: 1000 mSec Memory Limit : 32768 KB
 Problem Description Problem Description
有N個飛船進行比賽,它們的跑道為直線并互相平行。每個飛船的起跑位置均不相同。第i個飛船從起跑線右邊Xi處開始向右行駛(Xi各不相同)。比賽開始后,它能在零時間內加速到最大速度Vi并永遠保持此速度。比賽沒有終點,即會永遠進行下去。

你的任務是算出比賽過程中一共有多少次"超車"。
 Input Input
輸入數據由多組數據組成。每組數據格式如下:
第一行為一個整數N(1<=N<=250000)。
接下來的N行,每行兩個整數Xi (0≤Xi≤10^6)和Vi(0<Vi<100),描述了一輛飛船的起跑位置和最大速度。
給出的飛船信息按照起跑位置Xi的升序排列,即X1<X2<X3<…<Xn。
最后一組數據N=0,標志輸入結束,不需要處理。
 Output Output
對于每組數據,輸出僅一行包含一個整數,即"超車"的次數對1000000的模。
 Sample Input Sample Input
4 0 2 2 1 3 8 6 3 0
 Sample Output Sample Output
2
#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
const int mod=1000000;
int v[102];
int main()
{
int x,a;
int n;
int sum;
while(scanf("%d",&n),n)
{
memset(v,0,sizeof(v));
sum=0;
for(int i=0;i<n;i++)
{
scanf("%d%d",&x,&a);
v[a]++;
for(int j=a+1;j<102;j++) sum+=v[j];
sum%=mod;
}
printf("%d\n",sum);
}
return 0;
}
文章來源: http://www.cnblogs.com/kuangbin/archive/2011/11/14/2248202.html
最優連通子集
| Time Limit: 1000MS |
|
Memory Limit: 10000K |
| Total Submissions: 1649 |
|
Accepted: 855 |
Description
眾所周知,我們可以通過直角坐標系把平面上的任何一個點P用一個有序數對(x, y)來唯一表示,如果x, y都是整數,我們就把點P稱為整點,否則點P稱為非整點。我們把平面上所有整點構成的集合記為W。
定義1 兩個整點P1(x1, y1), P2(x2, y2),若|x1-x2| + |y1-y2| = 1,則稱P1, P2相鄰,記作P1~P2,否則稱P1, P2不相鄰。
定義 2 設點集S是W的一個有限子集,即S = {P1, P2,..., Pn}(n >= 1),其中Pi(1 <= i <= n)屬于W,我們把S稱為整點集。
定義 3 設S是一個整點集,若點R, T屬于S,且存在一個有限的點序列Q1, Q2, ?, Qk滿足:
1. Qi屬于S(1 <= i <= k);
2. Q1 = R, Qk = T;
3. Qi~Qi + 1(1 <= i <= k-1),即Qi與Qi + 1相鄰;
4. 對于任何1 <= i < j <= k有Qi ≠ Qj;
我們則稱點R與點T在整點集S上連通,把點序列Q1, Q2,..., Qk稱為整點集S中連接點R與點T的一條道路。
定義4 若整點集V滿足:對于V中的任何兩個整點,V中有且僅有一條連接這兩點的道路,則V稱為單整點集。
定義5 對于平面上的每一個整點,我們可以賦予它一個整數,作為該點的權,于是我們把一個整點集中所有點的權的總和稱為該整點集的權和。
我們希望對于給定的一個單整點集V,求出一個V的最優連通子集B,滿足:
1. B是V的子集
2. 對于B中的任何兩個整點,在B中連通;
3. B是滿足條件(1)和(2)的所有整點集中權和最大的。
Input
第1行是一個整數N(2 <= N <= 1000),表示單整點集V中點的個數;
以下N行中,第i行(1 <= i <= N)有三個整數,Xi, Yi, Ci依次表示第i個點的橫坐標,縱坐標和權。同一行相鄰兩數之間用一個空格分隔。-10^6 <= Xi, Yi <= 10^6;-100 <= Ci <= 100。
Output
僅一個整數,表示所求最優連通集的權和。
Sample Input
5
0 0 -2
0 1 1
1 0 1
0 -1 1
-1 0 1
Sample Output
2
Source
/*********************************************
POJ1192最優連通子集
題目意思:如果兩個點的距離相差一,則兩個點相鄰或著說連通。
求:連通圖的最大加權和。
思路:對給出的 n 個點建樹,然后就是灰常簡單的樹形DP了。
f[ p ] 表示節點 p 含有的最大值,最后用個for循環遍歷各個節點找出最大加權和。
**********************************************/
#include<iostream>
#include<stdio.h>
#include<vector>
#include<math.h>
using namespace std;
const int MAXN=1005;
int n;
bool used[MAXN];
int f[MAXN];
struct Node
{
int x,y,v;
}tt[MAXN];
vector<int>child[MAXN];
bool near(int p,int q)//判斷兩個整點是否相鄰
{
if(fabs((double)tt[p].x-tt[q].x)+fabs((double)tt[p].y-tt[q].y)==1)return true;
return false;
}
void dfs(int p)
{
used[p]=true;
for(int i=1;i<=n;i++)
{
if(!used[i]&&near(p,i))
{
child[p].push_back(i);
dfs(i);
}
}
}
void recur(int p)
{
if(child[p].size()==0)
{
f[p]=tt[p].v;
return;
}
for(int i=0;i<child[p].size();i++)
recur(child[p][i]);
f[p]=tt[p].v;
for(int i=0;i<child[p].size();i++)
if(f[child[p][i]]>0)f[p]+=f[child[p][i]];
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d%d",&tt[i].x,&tt[i].y,&tt[i].v);
for(int i=1;i<=n;i++) child[i].clear();
memset(used,false,sizeof(used));
dfs(1);
recur(1);
int ans=0;
//for(int i=1;i<=n;i++)
//if(f[i]>ans)ans=f[i];
printf("%d\n",f[1]);
system("pause");
return 0;
}
文章來源: http://www.cnblogs.com/kuangbin/archive/2011/11/13/2247173.html
Break the Chocolate
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 427 Accepted Submission(s): 142
Problem Description
 Benjamin is going to host a party for his big promotion coming up. Every party needs candies, chocolates and beer, and of course Benjamin has prepared some of those. But as everyone likes to party, many more people showed up than he expected. The good news is that candies are enough. And for the beer, he only needs to buy some extra cups. The only problem is the chocolate. As Benjamin is only a 'small court officer' with poor salary even after his promotion, he can not afford to buy extra chocolate. So he decides to break the chocolate cubes into smaller pieces so that everyone can have some. He have two methods to break the chocolate. He can pick one piece of chocolate and break it into two pieces with bare hand, or put some pieces of chocolate together on the table and cut them with a knife at one time. You can assume that the knife is long enough to cut as many pieces of chocolate as he want. The party is coming really soon and breaking the chocolate is not an easy job. He wants to know what is the minimum number of steps to break the chocolate into unit-size pieces (cubes of size 1 × 1 × 1). He is not sure whether he can find a knife or not, so he wants to know the answer for both situations.
Input
The first line contains an integer T(1<= T <=10000), indicating the number of test cases.
Each test case contains one line with three integers N,M,K(1 <=N,M,K <=2000), meaning the chocolate is a cube of size N ×M × K.
Output
For each test case in the input, print one line: "Case #X: A B", where X is the test case number (starting with 1) , A and B are the minimum numbers of steps to break the chocolate into N × M × K unit-size pieces with bare hands and knife respectively.
Sample Input
Sample Output
Case #1: 2 2 Case #2: 7 3
Source
初看感覺非常簡單,但是陷阱很多!!!!!!
先把N,M,K從小到大排序。
然后用手扮的次數就是:(N-1)+N*(M-1+M*(K-1))=N*M*K-1;
就是先扮截面積最大的面,就是分最小的N,要N-1次,之后就有了N個M*K了,類似辦法,要M-1+M*(K-1);
但是這里一定要用long long ,int會超出的。(這里注意,比賽果然不一樣,陷阱很多,下次注意了)
然后用到的時候。其實是分別切N,M,K。
切N是要[log2(N)]往上取整。往上取整我是加了0.999,不知道大牛們有沒有更好的辦法!!有的話請留言噢~~~~
切M和K類似。
具體看代碼:
#include<stdio.h>
#include<math.h>
int main()
{
int T;
int iCase=0;
int n,m,k;
scanf("%d",&T);
while(T--)
{
iCase++;
scanf("%d%d%d",&n,&m,&k);
int t1=n,t2,t3=n;
if(m<t1)t1=m;
if(k<t1)t1=k;
if(m>t3)t3=m;
if(k>t3)t3=k;
t2=n+m+k-t1-t3;
n=t1;m=t2;k=t3;
int res=0;
if(n>1)res+=(int)(log(1.0*n)/log(2.0)+0.999);//往上取整
if(m>1)res+=(int)(log(1.0*m)/log(2.0)+0.999);
if(k>1)res+=(int)(log(1.0*k)/log(2.0)+0.999);
long long res1=(long long)n*m*k-1;
printf("Case #%d: %I64d %d\n",iCase,res1,res);
}
return 0;
}
文章來源: http://www.cnblogs.com/kuangbin/archive/2011/11/12/2246500.html
Fast Food
| Time Limit: 1000MS |
|
Memory Limit: 10000K |
| Total Submissions: 1597 |
|
Accepted: 553 |
|
Special Judge |
Description
The fastfood chain McBurger owns several restaurants along a highway. Recently, they have decided to build several depots along the highway, each one located at a restaurant and supplying several of the restaurants with the needed ingredients. Naturally, these depots should be placed so that the average distance between a restaurant and its assigned depot is minimized. You are to write a program that computes the optimal positions and assignments of the depots.
To make this more precise, the management of McBurger has issued the following specification: You will be given the positions of n restaurants along the highway as n integers d1 < d2 < ... < dn (these are the distances measured from the company's headquarter, which happens to be at the same highway). Furthermore, a number k (k <= n) will be given, the number of depots to be built.
The k depots will be built at the locations of k different restaurants. Each restaurant will be assigned to the closest depot, from which it will then receive its supplies. To minimize shipping costs, the total distance sum, defined as
n
∑ |di - (position of depot serving restaurant i)|
i=1
must be as small as possible.
Write a program that computes the positions of the k depots, such that the total distance sum is minimized.
Input
The input file contains several descriptions of fastfood chains. Each description starts with a line containing the two integers n and k. n and k will satisfy 1 <= n <= 200, 1 <= k <= 30, k <= n. Following this will n lines containing one integer each, giving the positions di of the restaurants, ordered increasingly.
The input file will end with a case starting with n = k = 0. This case should not be processed.
Output
For each chain, first output the number of the chain. Then output an optimal placement of the depots as follows: for each depot output a line containing its position and the range of restaurants it serves. If there is more than one optimal solution, output any of them. After the depot descriptions output a line containing the total distance sum, as defined in the problem text.
Output a blank line after each test case.
Sample Input
6 3
5
6
12
19
20
27
0 0
Sample Output
Chain 1
Depot 1 at restaurant 2 serves restaurants 1 to 3
Depot 2 at restaurant 4 serves restaurants 4 to 5
Depot 3 at restaurant 6 serves restaurant 6
Total distance sum = 8
Source
【題目大意】
一條公路上有n個旅館,選出其中k個設置倉庫,一個倉庫可服務若干個旅館,一個旅館只需一個倉庫服務。問在哪幾個旅館設置倉庫,每個倉庫服務哪些旅館,可使得旅館到倉庫的總距離最小,并求出總距離(長理只要求求最后一步)。
【數據范圍】
1 <= n <= 200, 1 <= k <= 30, k <= n
【解題思想】
1、此題屬于明顯動態規劃題,關鍵點是找狀態轉移方程。
2、可以用sum[i][j]表示前i個旅館,設置j個倉庫得到的距離和最小值,那么sum[n][k]即為所求。
3、找sum[i][j]的子結構,假設前j-1個倉庫服務第1個到第k個旅館,則最后一個倉庫服務第k+1個到第i個旅館。
4、可以用one[i][j]表示一個倉庫服務第i個到第j個旅館,到這個倉庫距離和的最小值。
5、則得到狀態轉移方程:sum[i][j]=min(sum[k][j-1]+one[k+1][i]) (j-1<=k<=i-1,min表示所有k取值得到的值中的最小值)。
6、問題轉換為了求one[i][j],即在第i到第j家旅館中設置一個倉庫的總距離。
7、假設i到j共有奇數家旅館,我們嘗試將倉庫放置在中間旅館,即旅館(i+j)/2,假設將倉庫左移距離x,則右半邊所有旅館到倉庫距離均加x,而只有部分左半邊旅館距離減少了x,剩下的減少均小于x,甚至不減少。因此可以得到,將倉庫從中間位置左移到任何位置總距離都會增加,右移同理,因此倉庫放到旅館(i+j)/2最合適。
8、假設i到j共有偶數家旅館,容易得到將倉庫放到(i+j-1)/2和(i+j+1)/2得到的總距離相等(對稱性),若將倉庫放到(i+j-1)/2,并左移,則用7相似的想法可得知總距離增大,右移情況同理,由此得知倉庫放到(i+j-1)/2這個位置即可滿足總距離最小。
9、由7、8得到one[i][j]實際上時將倉庫放到(i+j)/2取整位置可得到最小的總距離。
10、數據范圍較小,我們可以計算出一切one[i][j]的組合。
11、由于poj還要求輸出在哪幾個旅館設置倉庫,每個倉庫服務哪些旅館,因此還需要存儲動態規劃路徑。
12、可用at[i][j],from[i][j],to[i][j]分別表示sum[i][j]得到最小值時最后一個倉庫的位置、服務的起始位置和服務的終止位置。
13、通過遞歸輸出結果。
#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
const int INF=100000000;
int r[300],sum[300][40],one[300][300];
int from[300][40],to[300][40],at[300][40];
int output(int i,int j)
{
if(j<=0||i<=0)return 1;
int num=output(from[i][j]-1,j-1);
printf("Depot %d at restaurant %d serves ",num,at[i][j]);
if(from[i][j]==to[i][j])printf("restaurant %d\n",from[i][j]);
else printf("restaurants %d to %d\n",from[i][j],to[i][j]);
return num+1;
}
int main()
{
int n,K,i,j,k,middle;
int iCase=0;
while(scanf("%d%d",&n,&K)!=EOF)
{
iCase++;
if(n==0&&K==0)break;
for(i=1;i<=n;i++)scanf("%d",&r[i]);
memset(one,0,sizeof(one));
memset(sum,0,sizeof(sum));
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
middle=(i+j)/2;
for(k=i;k<middle;k++)one[i][j]+=r[middle]-r[k];
for(k=middle+1;k<=j;k++)one[i][j]+=r[k]-r[middle];
}
}
for(i=1;i<=n;i++)sum[i][0]=INF;
for(i=1;i<=n;i++)
{
for(j=1;j<=i&&j<=K;j++)
{
sum[i][j]=INF;
for(k=j-1;k<=i-1;k++)
{
int tmp=sum[k][j-1]+one[k+1][i];
if(tmp<sum[i][j])
{
sum[i][j]=tmp;
from[i][j]=k+1;
to[i][j]=i;
at[i][j]=(k+1+i)/2;
}
}
}
}
printf("Chain %d\n",iCase);
output(n,K);
printf("Total distance sum = %d\n\n",sum[n][K]);
}
return 0;
}
文章來源: http://www.cnblogs.com/kuangbin/archive/2011/11/12/2246407.html
Counterfeit Dollar
| Time Limit: 1000MS |
|
Memory Limit: 10000K |
| Total Submissions: 30917 |
|
Accepted: 9680 |
Description
Sally Jones has a dozen Voyageur silver dollars. However, only eleven of the coins are true silver dollars; one coin is counterfeit even though its color and size make it indistinguishable from the real silver dollars. The counterfeit coin has a different weight from the other coins but Sally does not know if it is heavier or lighter than the real coins.
Happily, Sally has a friend who loans her a very accurate balance scale. The friend will permit Sally three weighings to find the counterfeit coin. For instance, if Sally weighs two coins against each other and the scales balance then she knows these two coins are true. Now if Sally weighs
one of the true coins against a third coin and the scales do not balance then Sally knows the third coin is counterfeit and she can tell whether it is light or heavy depending on whether the balance on which it is placed goes up or down, respectively.
By choosing her weighings carefully, Sally is able to ensure that she will find the counterfeit coin with exactly three weighings.
Input
The first line of input is an integer n (n > 0) specifying the number of cases to follow. Each case consists of three lines of input, one for each weighing. Sally has identified each of the coins with the letters A--L. Information on a weighing will be given by two strings of letters and then one of the words ``up'', ``down'', or ``even''. The first string of letters will represent the coins on the left balance; the second string, the coins on the right balance. (Sally will always place the same number of coins on the right balance as on the left balance.) The word in the third position will tell whether the right side of the balance goes up, down, or remains even.
Output
For each case, the output will identify the counterfeit coin by its letter and tell whether it is heavy or light. The solution will always be uniquely determined.
Sample Input
1
ABCD EFGH even
ABCI EFJK up
ABIJ EFGH even
Sample Output
K is the counterfeit coin and it is light.
Source
枚舉了所有的情況。12種,有一種假的,輕就設為-1,重為1,其余為0,至多12*2中情況。
#include<stdio.h>
#include<string.h>
int main()
{
char str[9][20];
int a[12];
int T;
scanf("%d",&T);
while(T--)
{
for(int i=0;i<9;i++)scanf("%s",&str[i]);
int res=-1;
while(res<12)
{
int t;
if(res==-1){res=0;t=1;}
else if(a[res]==1) t=-1;
else {res++;t=1;}
for(int i=0;i<12;i++) a[i]=0;
a[res]=t;
int L=0,R=0;
int len=strlen(str[0]);
for(int i=0;i<len;i++) L+=a[str[0][i]-'A'];
len=strlen(str[1]);
for(int i=0;i<len;i++) R+=a[str[1][i]-'A'];
if(strcmp(str[2],"even")==0)
{
if(L!=R)continue;
}
if(strcmp(str[2],"up")==0)
if(L<=R)continue;
if(strcmp(str[2],"down")==0)
if(L>=R)continue;
L=0,R=0;
len=strlen(str[3]);
for(int i=0;i<len;i++) L+=a[str[3][i]-'A'];
len=strlen(str[4]);
for(int i=0;i<len;i++) R+=a[str[4][i]-'A'];
if(strcmp(str[5],"even")==0)
{
if(L!=R)continue;
}
if(strcmp(str[5],"up")==0)
if(L<=R)continue;
if(strcmp(str[5],"down")==0)
if(L>=R)continue;
L=0,R=0;
len=strlen(str[6]);
for(int i=0;i<len;i++) L+=a[str[6][i]-'A'];
len=strlen(str[7]);
for(int i=0;i<len;i++) R+=a[str[7][i]-'A'];
if(strcmp(str[8],"even")==0)
{
if(L!=R)continue;
}
if(strcmp(str[8],"up")==0)
if(L<=R)continue;
if(strcmp(str[8],"down")==0)
if(L>=R)continue;
break;
}
printf("%c is the counterfeit coin and it is ",res+'A');
if(a[res]==-1) printf("light.\n");
else printf("heavy.\n");
}
return 0;
}
文章來源: http://www.cnblogs.com/kuangbin/archive/2011/11/12/2246372.html
Zombie’s Treasure Chest
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 994 Accepted Submission(s): 211
Problem Description
Some brave warriors come to a lost village. They are very lucky and find a lot of treasures and a big treasure chest, but with angry zombies.
The warriors are so brave that they decide to defeat the zombies and then bring all the treasures back. A brutal long-drawn-out battle lasts from morning to night and the warriors find the zombies are undead and invincible.
Of course, the treasures should not be left here. Unfortunately, the warriors cannot carry all the treasures by the treasure chest due to the limitation of the capacity of the chest. Indeed, there are only two types of treasures: emerald and sapphire. All of the emeralds are equal in size and value, and with infinite quantities. So are sapphires.
Being the priest of the warriors with the magic artifact: computer, and given the size of the chest, the value and size of each types of gem, you should compute the maximum value of treasures our warriors could bring back.
Input
There are multiple test cases. The number of test cases T (T <= 200) is given in the first line of the input file. For each test case, there is only one line containing five integers N, S1, V1, S2, V2, denoting the size of the treasure chest is N and the size and value of an emerald is S1 and V1, size and value of a sapphire is S2, V2. All integers are positive and fit in 32-bit signed integers.
Output
For each test case, output a single line containing the case number and the maximum total value of all items that the warriors can carry with the chest.
Sample Input
2 100 1 1 2 2 100 34 34 5 3
Sample Output
Source
Recommend
lcy
#include<stdio.h>
#include<algorithm>
using namespace std;
long long gcd(long long da,long long xiao)
{
long long temp;
while(xiao!=0)
{
temp=da%xiao;
da=xiao;
xiao=temp;
}
return da;
}
int main()
{
int iCase=0;
int T;
scanf("%d",&T);
long long N,S1,V1,S2,V2;
while(T--)
{
iCase++;
scanf("%I64d%I64d%I64d%I64d%I64d",&N,&S1,&V1,&S2,&V2);
long long tmp=S1*S2/gcd(S1,S2);
long long res;
long long tt=N/tmp;
N=N%tmp;
if(tt)
{
tt--;
N+=tmp;
}
res=max((tt)*(tmp/S1)*V1,(tt)*(tmp/S2)*V2);
long long res2=0;
if(S2>S1)
{
long long t;
t=S1;S1=S2;S2=t;
t=V1;V1=V2;V2=t;
}
for(int i=0;i<=N/S1;i++)
{
if(res2<i*V1+(N-i*S1)/S2*V2)res2=i*V1+(N-i*S1)/S2*V2;
}
res+=res2;
printf("Case #%d: %I64d\n",iCase,res);
}
return 0;
}
文章來源: http://www.cnblogs.com/kuangbin/archive/2011/11/07/2240182.html
What Is Your Grade?
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4032 Accepted Submission(s): 1198
Problem Description
“Point, point, life of student!”
This is a ballad(歌謠)well known in colleges, and you must care about your score in this exam too. How many points can you get? Now, I told you the rules which are used in this course.
There are 5 problems in this final exam. And I will give you 100 points if you can solve all 5 problems; of course, it is fairly difficulty for many of you. If you can solve 4 problems, you can also get a high score 95 or 90 (you can get the former(前者) only when your rank is in the first half of all students who solve 4 problems). Analogically(以此類推), you can get 85、80、75、70、65、60. But you will not pass this exam if you solve nothing problem, and I will mark your score with 50.
Note, only 1 student will get the score 95 when 3 students have solved 4 problems.
I wish you all can pass the exam!
Come on!
Input
Input contains multiple test cases. Each test case contains an integer N (1<=N<=100, the number of students) in a line first, and then N lines follow. Each line contains P (0<=P<=5 number of problems that have been solved) and T(consumed time). You can assume that all data are different when 0<p.
A test case starting with a negative integer terminates the input and this test case should not to be processed.
Output
Output the scores of N students in N lines for each case, and there is a blank line after each case.
Sample Input
4 5 06:30:17 4 07:31:27 4 08:12:12 4 05:23:13 1 5 06:30:17 -1
Sample Output
Author
lcy
#include<stdio.h>
#include<algorithm>
#include<stdlib.h>//qsort
#include<iostream>
#include<string.h>
using namespace std;
struct Node
{
int num;//輸入的原始編號
int n;//正確解題數
int fen;//分數
int time;//用掉的時間
}node[110];
int cmp1(const void *a,const void *b)
{
struct Node *c=(Node *)a;
struct Node *d=(Node *)b;
if(c->n == d->n)return c->time - d->time;
return d->n - c->n;
}
int cmp2(const void *a,const void *b)
{
struct Node *c=(Node *)a;
struct Node *d=(Node *)b;\
return c->num - d->num;
}
int main()
{
int n,i,j,k;
int sum[10];
int tol[10];
int h,m,s;
while(scanf("%d",&n))
{
if(n<0)break;
memset(sum,0,sizeof(sum));
memset(tol,0,sizeof(tol));
for(i=0;i<n;i++)
{
scanf("%d %d:%d:%d",&node[i].n,&h,&m,&s);
node[i].num=i;
node[i].time=h*3600+m*60+s;
sum[node[i].n]++;
}
for(i=4;i>0;i--)
{
tol[i]=tol[i+1];
tol[i]+=sum[i+1];
}
qsort(node,n,sizeof(node[0]),cmp1);
for(i=0;i<n;i++)
{
node[i].fen=node[i].n*10+50;
if(node[i].n>=1&&node[i].n<5&&(((i+1)-tol[node[i].n])<=sum[node[i].n]/2)) node[i].fen+=5;
}
qsort(node,n,sizeof(node[0]),cmp2);
for(i=0;i<n;i++)
{
printf("%d\n",node[i].fen);
}
printf("\n");
}
return 0;
}
文章來源: http://www.cnblogs.com/kuangbin/archive/2011/11/01/2232037.html
|
|
|
| | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
|---|
| 31 | 1 | 2 | 3 | 4 | 5 | 6 | | 7 | 8 | 9 | 10 | 11 | 12 | 13 | | 14 | 15 | 16 | 17 | 18 | 19 | 20 | | 21 | 22 | 23 | 24 | 25 | 26 | 27 | | 28 | 29 | 30 | 31 | 1 | 2 | 3 | | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
公告
導航
統計
- 隨筆: 100
- 文章: 0
- 評論: 2
- 引用: 0
常用鏈接
留言簿(2)
隨筆分類
隨筆檔案
博客
搜索
最新評論

閱讀排行榜
評論排行榜
|
|