/*
題意：就是給你一個有2^n個輸入的門電路，初始輸入為全0，問至少要改變輸入
開關多少次（即改變輸入中0、1多少次）才能得到所需的0、1輸出序列。

題意分析：

這道題的數據范圍為k<10000，所以不能枚舉暴搞，只能用遞推來求解。

仔細分析就可一發現當有多個0或多個1在一起時，是不用改變開關的。只有
在輸出序列中出現0到1或1到0的跳變時才需要改變開關。


*/

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int ch[10010];
char str[10010];
int n;
int solve(int i)//遞歸求從0變1需要的至少次數 
{
    if(2*i+1>=n-1)
    {
        if(ch[i]==0)return 1;
        else return 2;
    }    
    if(ch[i]==1) return solve(2*i+1)+solve(2*i+2);
    else return min(solve(2*i+1),solve(2*i+2));
}    
int main()
{
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        scanf("%s",&str);
        for(int i=0;i<n-1;i++)
        {
            scanf("%d",&ch[i]);
        }
        int m=solve(0);
        //printf("%d\n",m);
        int res;
        if(str[0]=='0') res=0;
        else res=1;
        int len=strlen(str);
        for(int i=1;i<len;i++)//找變化的次數，1變0，0變1 
        {
            if(str[i]!=str[i-1])res++;
        }        
        if(res)res+=m-1;//加上第一次變1 的次數，以后改變只需要一次就好了 
        printf("%d\n",res);
    }    
    return 0;
}
 
 
 
1A,好爽，去福州前去刷刷水題很痛快。。。。期待福州拿牌回來。。。

Sheryl's Circuit I
Time Limit: 1000MS   Memory Limit: 65536K
Total Submissions: 1037   Accepted: 430

Description

In the Design of Digital Logic class, Sheryl is asked to design a device which can produce a digital signal (a sequence of 0 and 1), given by the professor. After several sleepless nights, she completes a kind of Boolean circuit which looks like a complete binary tree as showed in Figure 1. Every node of the tree is a Boolean arithmetic unit (BAU) which takes in inputs from its both children and produce an output to its parent. The inputs of BAU are either 1 or 0, and the output should be calculated due to the type of BAU which is either ∧ or ∨. The truth tables of the two types are also showed in Figure 1. The INPUT of Sheryl's circuit is the sequence of inputs of the lowest-level BAUs and the OUTPUT is the output of the top BAU.

 


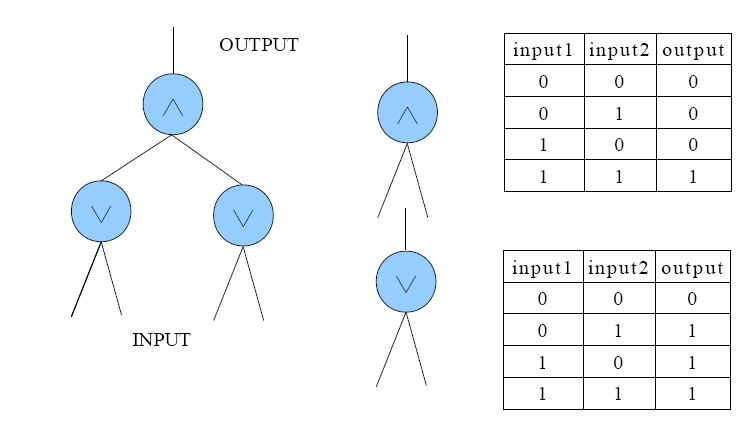
Figure 1

 

To accomplish the assignment, Sheryl has to manually handle the INPUT to produce the expected signal. For example, assuming Sheryl's circuit is the one showed in Figure 1, when the professor wants (0, 0, 0, 1, 1, 1) as the signal, the INPUT may alter as this: (0, 0, 0, 0) -> (0, 0, 1, 1) -> (1, 1, 0, 0) -> (1, 1, 1, 1) -> (1, 0, 1, 0) -> (0, 1, 0, 1). But this is too complex because Sheryl has to change the INPUT 14(2 + 4 + 2 + 2 + 4) times totally! So a more clever way is preferable, say (0, 0, 0, 0) -> (0, 0, 0, 0) -> (0, 0, 0, 0) -> (0, 1, 0, 1) -> (0, 1, 0, 1) -> (0, 1, 0, 1), which requires only 2(0 + 0 + 2 + 0 +0) changes of the INPUT.

Given Sheryl's circuit and the signal expected, your task is to find the minimal changes of the INPUT to produce the signal. Note the INPUT begins with all 0s.

Input

There are multiple test cases.
The first line contains the number of test cases.
Each test case begins with an integer N( ≤ 10000), the number of inputs of Sheryl's circuit. It is guaranteed that N equals 2k, where k is an integer.
The next line contains the expected signal which consists of 0 and 1 only. The length of the signal is no more than 10000.
Next N - 1 numbers describe the types of the BAUs, 0 for ∨ and 1 for ∧. The describing order is from top level to bottom level. For the same level it is from left to right.

Output

For each test case output the minimal number of changes in a separate line.

Sample Input

2
4
010101
0 0 0
4
111111
1 1 1

Sample Output

5
4

Source

 
 
題意：就是給你一個有2^n個輸入的門電路，初始輸入為全0，問至少要改變輸入開關多少次（即改變輸入中0、1多少次）才能得到所需的0、1輸出序列。

題意分析：

這道題的數據范圍為k<10000，所以不能枚舉暴搞，只能用遞推來求解。

仔細分析就可一發現當有多個0或多個1在一起時，是不用改變開關的。只有在輸出序列中出現0到1或1到0的跳變時才需要改變開關。

 
 

文章來源:http://www.cnblogs.com/kuangbin/archive/2011/11/14/2248770.html