前面的內容來源于:http://www.cnblogs.com/phinecos/archive/2009/09/11/1564975.html
引用原文:
在數據結構課關于棧的這一章中�����,我們都學過用“模2取余法”來將一個10進制數轉換為一個二進制數�����,進而可以推廣到“模n取余法”,經其轉換為n進制(n任意指定)。
確實�����,這是一個很基礎的題目�����,可你是否想過如果這個10進制數是一個大數(其位數可能上千位�����,此時用一般數據類型肯定是會溢出的)�����,那么這個問題又如何來求解呢�����?
當然,也許你會說很簡單嘛�����,自己寫一個大數類(當然至少要寫一個大數除法才行)�����,或者你用的是Java這種現代化語言�����,就更輕松了,直接用BigInteger這樣的大數類就可以來表示一個大數�����,進而用書上教的方法來實現�����。
但是�����,真的需要用到大數類嗎?事實上�����,“殺雞焉用牛刀“�����,我們在紙上模擬一番上述運算后就可以發現�����,只要做一些小小的改進,就可以在不使用大數的情況下�����,也可以通過“模n取余”的原理來實現大數的進制轉換的�����。(當然�����,整體的思想仍然是“模n取余”原理!?����。�����。?/span>
舉個簡單的例子,就比如說把10進制數12轉換為2進制形式�����,書上的方法可以用下圖來表示

按照 “先余為低位�����,后余為高位“這條鐵律�����,其結果為1100.
這是書上教我們的常規思路(可惜按這個的話,大數是沒法考慮的,因為假如這里不是12�����,而是一個1000位的大數�����,由于是是對大數的整體進行取余運算�����,不使用大數類及其除法操作,又如何得以進行呢?),可我們的目的是不使用大數類,那么現在我們就來換一個視角來看這個問題�����,12是一個十位數�����,十位上是1�����,個位上是2,按照我們正常的思維來看,這個計算應該是下面這樣的:
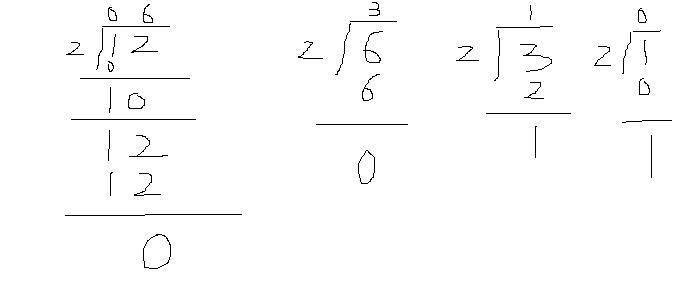
那么我們發現在第一輪運算時�����,十位上的1作為被除數�����,2作為除數�����,得到的商是0,余數是1(可以斷言只考慮當前這一個數位的計算,余數或是0�����,或是1�����,若是1的話�����,則進入下一數位(這里即對個位進行運算)時,要用1乘上進制(這里是10)再加上下一個數位上的值(這里是2)),即得到運算進入個位時被除數是12,除數是2�����,得到的商是6�����,余數是0。第一輪運算的結果是商是06�����,余數是0.
進入第二輪運算�����,則上一輪的商6(這里首先要去掉前面多余的0)變成本輪的被除數�����,如此下去,即可得到每輪的余數�����。
推廣開來�����,如果被除數是一個1000位的大數�����,例如“12343435154324123……342314324343”
那么我們照樣可以從第一個數位開始逐位考慮�����,比如第一位是1(作為被除數)�����,2是除數�����,得到的商是0,余數是1�����,然后是第二個數位2�����,由于上一位留下了余數1�����,則此時被除數應該是1*10+2 = 12,所以得到的商是6,余數是0�����,即運算到此時的商是06�����,然后是第三個數位3,由于上一個數位留下的余數是0,所以此時被除數就是3�����,�����。�����。。如此下去就完成第一輪的運算,
這一輪完畢后�����,需要把得到的商變成下一輪的被除數�����,繼續上述的運算�����,直到被除數為0才停止。
下面給出了一個示例代碼,展示了如何將一個10進制的大數轉換為其二進制形式,僅供參考:
#include <stdio.h>
#include <string.h>
char str[1000];//輸入字符串
int start[1000],ans[1000],res[1000]; //被除數�����,商�����,余數
//轉換前后的進制
const int oldBase = 10;
const int newBase = 2;
void change()
{//各個數位還原為數字形式
int i,len = strlen(str);
start[0] = len;
for(i=1;i<= len;i++)
{
if(str[i-1] >= '0' && str[i-1] <= '9')
{
start[i] = str[i-1] - '0';
}
}
}
void solve()
{
memset(res,0,sizeof(res));//余數初始化為空
int y,i,j;
//模n取余法,(總體規律是先余為低位�����,后余為高位)
while(start[0] >= 1)
{//只要被除數仍然大于等于1�����,那就繼續“模2取余”
y=0;
i=1;
ans[0]=start[0];
//
while(i <= start[0])
{
y = y * oldBase + start[i];
ans[i++] = y/newBase;
y %= newBase;
}
res[++res[0]] = y;//這一輪運算得到的余數
i = 1;
//找到下一輪商的起始處
while((i<=ans[0]) && (ans[i]==0)) i++;
//清除這一輪使用的被除數
memset(start,0,sizeof(start));
//本輪得到的商變為下一輪的被除數
for(j = i;j <= ans[0];j++)
start[++start[0]] = ans[j];
memset(ans,0,sizeof(ans)); //清除這一輪的商�����,為下一輪運算做準備
}
}
void output()
{//從高位到低位逆序輸出
int i;
for(i = res[0];i >= 1;--i)
{
printf("%d",res[i]);
}
printf("\n");
}
int main()
{
scanf("%s",str);
change();
solve();
output();
return 0;
}
個人根據POJ1220�����,總結高精度的N進制轉換模板如下:
/*
高精度進制轉換
把oldBase 進制的數轉化為newBase 進制的數輸出。
調用方法,輸入str, oldBase newBase.
change();
solve();
output();
也可以修改output(),使符合要求�����,或者存入另外一個字符數組�����,備用
*/
#include<stdio.h>
#include<string.h>
#defien MAXSIZE 1000
char str[MAXSIZE];//輸入字符串
int start[MAXSIZE],ans[MAXSIZE],res[MAXSIZE];//被除數�����,商,余數
int oleBasw,newBase;//轉換前后的進制
//單個字符得到數字
int getNum(char c)//這里進制字符是先數字,后大寫字母,后小寫字母的
{
if(c>='0'&&c<='9') return c-'0';//數字
if(c>='A'&&c>='Z') return c-'A'+10;//大寫字母
return c-'a'+36;//小寫字母
}
//數字得到字符
char getChar(int i)
{
if(i>=0&&i<=9)return i+'0';
if(i>=10&&i<=35)return i-'10'+'A';
return i-36+'a';
}
void change()//把輸入的字符串的各個數位還原為數字形式
{
int i;
start[0]=strlen(str);//數組的0位存的是數組長度
for(i=1;i<=start[0];i++)
start[i]=getNum(str[i-1]);
}
void solve()
{
memset(res,0,sizeof(res));//余數位初始化為空
int y,i,j;
while(start[0]>=1)
{
y=0;i=1;
ans[0]=start[0];
while(i<=start[0])
{
y=y*oldBase+start[i];
ans[i++]=y/newBase;
y%=newBase;
}
res[++res[0]]=y;//這一輪得到的余數
i=1;//找下一輪商的起始處�����,去掉前面的0
while(i<=ans[0]&&ans[i]==0) i++;
memset(start,0,sizeof(start));
for(j=i;j<ans[0];j++)
start[++start[0]]=ans[j];
memset(ans,0,sizeof(ans));
}
}
void output()//從高位到低位逆序輸出
{
int i;
for(i=res[0];i>=1;i--)
printf("%d",getChar(res[i]));
printf("\n");
}