昨晚熱身，a了個(gè)背包，tle了搜索（好久沒(méi)練的），剩下的隊(duì)友出，早上出了博弈的
Northcott Game
Time Limit : 1000/1000ms (Java/Other) Memory Limit : 32768/32768K (Java/Other)
Total Submission(s) : 11 Accepted Submission(s) : 3
Font: Times New Roman | Verdana | Georgia
Font Size: ← →
Problem Description
Tom和Jerry正在玩一種Northcott游戲，可是Tom老是輸，因此他懷疑這個(gè)游戲是不是有某種必勝策略，郁悶的Tom現(xiàn)在向你求救了，你能幫幫他么？
游戲規(guī)則是這樣的：
如圖所示，游戲在一個(gè)n行m列（1 ≤ n ≤ 1000且2 ≤ m ≤ 100）的棋盤(pán)上進(jìn)行，每行有一個(gè)黑子（黑方）和一個(gè)白子（白方）。執(zhí)黑的一方先行，每次玩家可以移動(dòng)己方的任何一枚棋子到同一行的任何一個(gè)空格上，當(dāng)然這過(guò)程中不許越過(guò)該行的敵方棋子。雙方輪流移動(dòng)，直到某一方無(wú)法行動(dòng)為止，移動(dòng)最后一步的玩家獲勝。Tom總是先下（黑方）。圖1是某個(gè)初始局面，圖二是Tom移動(dòng)一個(gè)棋子后的局面（第一行的黑子左移兩步）。
圖1
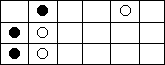
圖2Input
輸入數(shù)據(jù)有多組。每組數(shù)據(jù)第一行為兩個(gè)整數(shù)n和m，由空格分開(kāi)。接下來(lái)有n行，每行兩個(gè)數(shù)Ti，Ji (1 ≤ Ti, Ji ≤ m)分別表示Tom和Jerry在該行棋子所處的列數(shù)。
注意：各組測(cè)試數(shù)據(jù)之間有不定數(shù)量的空行。你必須處理到文件末。
Output
對(duì)于每組測(cè)試數(shù)據(jù)輸出一行你的結(jié)果。如果當(dāng)前局面下Tom有必勝策略則輸出“I WIN!”，否則輸出“BAD LUCK!”。
Sample Input
3 6
4 5
1 2
1 2
3 6
4 5
1 3
1 2
Sample Output
BAD LUCK!
I WIN!
/**//*
尼姆博奕(Nimm Game):
有三堆各若干個(gè)物品,兩個(gè)人輪流從某一堆取任意多的物品,規(guī)定每次至少取一個(gè),多者不限,最后取光者得勝.
這種情況最有意思,它與二進(jìn)制有密切關(guān)系,我們用(a,b,c)表示某種局勢(shì),首先(0,0,0)顯然是奇異局勢(shì),無(wú)論誰(shuí)面對(duì)奇異局勢(shì),都必然失敗.第二種奇異局勢(shì)是(0,n,n),只要與對(duì)手拿走一樣多的物品,最后都將導(dǎo)致(0,0,0).仔細(xì)分析一下,(1,2,3)也是奇異局勢(shì),無(wú)論對(duì)手如何拿,接下來(lái)都可以變?yōu)?0,n,n)的情形.
計(jì)算機(jī)算法里面有一種叫做按位模2加,也叫做異或的運(yùn)算,我們用符號(hào)(+)表示這種運(yùn)算.這種運(yùn)算和一般加法不同的一點(diǎn)是1+1=0.先看(1,2,3)的按位模2加的結(jié)果：
1 =二進(jìn)制01
2 =二進(jìn)制10
3 =二進(jìn)制11 (+)
-------
0 =二進(jìn)制00 (注意不進(jìn)位)
對(duì)于奇異局勢(shì)(0,n,n)也一樣,結(jié)果也是0.
任何奇異局勢(shì)(a,b,c)都有a(+)b(+)c =0.
如果我們面對(duì)的是一個(gè)非奇異局勢(shì)(a,b,c),要如何變?yōu)槠娈惥謩?shì)呢？假設(shè) a < b< c,我們只要將 c 變?yōu)?nbsp;a(+)b,即可,因?yàn)橛腥缦碌倪\(yùn)算結(jié)果: a(+)b(+)(a(+)b)=(a(+)a)(+)(b(+)b)=0(+)0=0.要將c 變?yōu)閍(+)b,只要從 c中減去 c-(a(+)b)即可.
*/
#include<iostream>
using namespace std;
#define MAXN 10001
int an[MAXN];
int Nimm_Game(int n)
{
int ans=0;
for(int i=0;i<n;++i){
ans^=an[i];
}
return ans;
}
int main()
{
int n,m,a,b;
while(scanf("%d %d",&n,&m) !=EOF)
{
for( int i=0;i<n;++i){
scanf("%d%d",&a,&b);
an[i]=abs(a-b)-1;
}
if(!Nimm_Game(n)) printf("BAD LUCK!\n");
else printf("I WIN!\n");
}
return 0;
}
posted on 2009-04-23 10:56
爬 閱讀(2386)
評(píng)論(0) 編輯 收藏 引用 所屬分類(lèi):
algorithm