Posted on 2010-10-15 11:15
MiYu 閱讀(2055)
評(píng)論(0) 編輯 收藏 引用 所屬分類:
ACM_資料

Matrix67原創(chuàng) Trackback: http://www.matrix67.com/blog/archives/108
如果說今年這時(shí)候OIBH問得最多的問題是二分圖,那么去年這時(shí)候問得最多的算是離散化了。對(duì)于“什么是離散化”,搜索帖子你會(huì)發(fā)現(xiàn)有各種說法,比如“排序后處理”、“對(duì)坐標(biāo)的近似處理”等等。哪個(gè)是對(duì)的呢?哪個(gè)都對(duì)。關(guān)鍵在于,這需要一些例子和不少的講解才能完全解釋清楚。
離散化是程序設(shè)計(jì)中一個(gè)非常常用的技巧,它可以有效的降低時(shí)間復(fù)雜度。其基本思想就是在眾多可能的情況中“只考慮我需要用的值”。下面我將用三個(gè)例子說明,如何運(yùn)用離散化改進(jìn)一個(gè)低效的,甚至根本不可能實(shí)現(xiàn)的算法。
《算法藝術(shù)與信息學(xué)競(jìng)賽》中的計(jì)算幾何部分,黃亮舉了一個(gè)經(jīng)典的例子,我認(rèn)為很適合用來介紹離散化思想。這個(gè)問題是UVA10173(http://acm.uva.es/p/v101/10173.html),題目意思很簡(jiǎn)單,給定平面上n個(gè)點(diǎn)的坐標(biāo),求能夠覆蓋所有這些點(diǎn)的最小矩形面積。這個(gè)問題難就難在,這個(gè)矩形可以傾斜放置(邊不必平行于坐標(biāo)軸)。
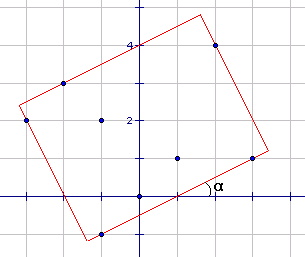
這里的傾斜放置很不好處理,因?yàn)槲覀儾恢肋@個(gè)矩形最終會(huì)傾斜多少度。假設(shè)我們知道這個(gè)矩形的傾角是α,那么答案就很簡(jiǎn)單了:矩形面積最小時(shí)四條邊一定都挨著某個(gè)點(diǎn)。也就是說,四條邊的斜率已經(jīng)都知道了的話,只需要讓這些邊從外面不斷逼近這個(gè)點(diǎn)集直到碰到了某個(gè)點(diǎn)。你不必知道這個(gè)具體應(yīng)該怎么實(shí)現(xiàn),只需要理解這可以通過某種方法計(jì)算出來,畢竟我們的重點(diǎn)在下面的過程。
我們的算法很顯然了:枚舉矩形的傾角,對(duì)于每一個(gè)傾角,我們都能計(jì)算出最小的矩形面積,最后取一個(gè)最小值。
這個(gè)算法是否是正確的呢?我們不能說它是否正確,因?yàn)樗静豢赡軐?shí)現(xiàn)。矩形的傾角是一個(gè)實(shí)數(shù),它有無數(shù)種可能,你永遠(yuǎn)不可能枚舉每一種情況。我們說,矩形的傾角是一個(gè)“連續(xù)的”變量,它是我們無法枚舉這個(gè)傾角的根本原因。我們需要一種方法,把這個(gè)“連續(xù)的”變量變成一個(gè)一個(gè)的值,變成一個(gè)“離散的”變量。這個(gè)過程也就是所謂的離散化。
我們可以證明,最小面積的矩形不但要求四條邊上都有一個(gè)點(diǎn),而且還要求至少一條邊上有兩個(gè)或兩個(gè)以上的點(diǎn)。試想,如果每條邊上都只有一個(gè)點(diǎn),則我們總可以把這個(gè)矩形旋轉(zhuǎn)一點(diǎn)使得這個(gè)矩形變“松”,從而有余地得到更小的矩形。于是我們發(fā)現(xiàn),矩形的某條邊的斜率必然與某兩點(diǎn)的連線相同。如果我們計(jì)算出了所有過兩點(diǎn)的直線的傾角,那么α的取值只有可能是這些傾角或它減去90度后的角(直線按“\”方向傾斜時(shí))這么C(n,2)種。我們說,這個(gè)“傾角”已經(jīng)被我們 “離散化”了。雖然這個(gè)算法仍然有優(yōu)化的余地,但此時(shí)我們已經(jīng)達(dá)到了本文開頭所說的目的。
對(duì)于某些坐標(biāo)雖然已經(jīng)是整數(shù)(已經(jīng)是離散的了)但范圍極大的問題,我們也可以用離散化的思想縮小這個(gè)規(guī)模。最近搞模擬賽Vijos似乎火了一把,我就拿兩道Vijos的題開刀。
VOJ1056(http://www.vijos.cn/Problem_Show.asp?id=1056) 永遠(yuǎn)是離散化的經(jīng)典問題。大意是給定平面上的n個(gè)矩形(坐標(biāo)為整數(shù),矩形與矩形之間可能有重疊的部分),求其覆蓋的總面積。平常的想法就是開一個(gè)與二維坐標(biāo)規(guī)模相當(dāng)?shù)亩SBoolean數(shù)組模擬矩形的“覆蓋”(把矩形所在的位置填上True)。可惜這個(gè)想法在這里有些問題,因?yàn)檫@個(gè)題目中坐標(biāo)范圍相當(dāng)大(坐標(biāo)范圍為-10^8到10^8之間的整數(shù))。但我們發(fā)現(xiàn),矩形的數(shù)量n<=100遠(yuǎn)遠(yuǎn)小于坐標(biāo)范圍。每個(gè)矩形會(huì)在橫縱坐標(biāo)上各“使用”兩個(gè)值, 100個(gè)矩形的坐標(biāo)也不過用了-10^8到10^8之間的200個(gè)值。也就是說,實(shí)際有用的值其實(shí)只有這么幾個(gè)。這些值將作為新的坐標(biāo)值重新劃分整個(gè)平面,省去中間的若干坐標(biāo)值沒有影響。我們可以將坐標(biāo)范圍“離散化”到1到200之間的數(shù),于是一個(gè)200*200的二維數(shù)組就足夠了。實(shí)現(xiàn)方法正如本文開頭所說的“排序后處理”。對(duì)橫坐標(biāo)(或縱坐標(biāo))進(jìn)行一次排序并映射為1到2n的整數(shù),同時(shí)記錄新坐標(biāo)的每?jī)蓚€(gè)相鄰坐標(biāo)之間在離散化前實(shí)際的距離是多少。這道題同樣有優(yōu)化的余地。
最后簡(jiǎn)單講一下計(jì)算幾何以外的一個(gè)運(yùn)用實(shí)例(實(shí)質(zhì)仍然是坐標(biāo)的離散)。才考的VOJ1238(http://www.vijos.cn/Problem_Show.asp?id=1238)中,標(biāo)程開了一個(gè)與時(shí)間范圍一樣大的數(shù)組來儲(chǔ)存時(shí)間段的位置。這種方法在空間上來看十分危險(xiǎn)。一旦時(shí)間取值范圍再大一點(diǎn),盲目的空間開銷將導(dǎo)致Memory Limit Exceeded。我們完全可以采用離散化避免這種情況。我們對(duì)所有給出的時(shí)間坐標(biāo)進(jìn)行一次排序,然后同樣用時(shí)間段的開始點(diǎn)和結(jié)束點(diǎn)來計(jì)算每個(gè)時(shí)刻的游戲數(shù),只是一次性加的經(jīng)驗(yàn)值數(shù)將乘以排序后這兩個(gè)相鄰時(shí)間點(diǎn)的實(shí)際差。這樣,一個(gè)1..n的數(shù)組就足夠了。
離散化的應(yīng)用相當(dāng)廣泛,以后你會(huì)看到還有很多其它的用途。
2007.04.05補(bǔ)充:
VOJ1056那個(gè)例子看來還是有人不明白。
我發(fā)一張示意圖,注意左邊的10*7的數(shù)組是如何等價(jià)地轉(zhuǎn)化為右邊兩個(gè)4*4的數(shù)組的
