ÒÇÇÒÇÇÕàêÕüçÞ«¥a2 = t, Úóÿþø«¥lÖÕ«Üõ║åÚÇƵĿÕà│þ│╗ÕQÜAn = 2 * t * An-1 - An-2 (n > 2)ÕQîÕêØÕÇ╝A1 = 1, A2 = tÕQøÚóÿþø«Þªüµ▒éSn = An ^ 2 + An-1 ^ 2 + ... + A1 ^ 2ÒÇ?br>ÒÇÇÒÇÇÕÅìÕñìÕ║öþö¿ÚÇƵĿÕà│þ│╗Õ¥ùÕê░ÕQ?br>ÒÇÇÒÇÇ
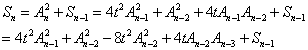
ÒÇÇÒÇÇþäÂÕÉÄSn-1Õê®þö¿þø©ÕÉîþÜäµû╣Õ╝ÅÕ▒òÕ╝ÇÕQîµèè4tAn-2An-3¥UªÕÄ╗ÕQîÕ¥ùÕêÄ═╝Ü
ÒÇÇÒÇÇ
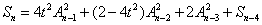
ÒÇÇÒÇÇÿqÖµáÀ׫▒µ»öÞ¥âÕ«╣µÿôÕ¥ùÕç║SnþÜäÚÇÜÚí╣ÕQ?br>ÒÇÇÒÇÇ
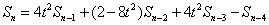
ÒÇÇÒÇÇÕ¢ôÕêØÿqÖõ©¬Úóÿþø«õ╣ïµëÇõ╗ѵ▓íµâø_ê░ÿqÖþºìµûÊÄ│òÕQîÕ░▒µÿ»Õøáõ©ÌZ©Çþ£ïÕê░ÚÇƵĿÕà│þ│╗ÕQîÕ░▒µâ│þØÇþö¿õ©ÇÞê¼Þºúµû╣þ¿ïþÜäµû╣µ│òÕÄ╗µ▒éÞºúÚÇÜÚí╣ÕQîµÇØþ╗┤Þó½Õ▒ÇÚÖÉõ║åÕQîÕàÂÕ«×þö¿¢ÄÇÕìòþÜäµû╣Õ╝Å׫▒ÕÅ»õ╗ѵĿÕç║µØÑþÜäÒÇéõ╗ÑÕÉÄÕ»╣õ║Äõ©Çõ©¬Úù«Úóÿ´╝îÕ║öÞ»Ñõ╗ÄÕñÜõ©¬µû╣ÚØóÕÄ╗µâ╗I╝îõ©ìÞ⢵âø_¢ôþäÂÕòèÒÇéµâ│ÞÁõh£Çÿqæþ£ïÕê░þÜäõ©ÇîDÁÞ»ØÕQîõ╗ѵ¡ñÞç¬Õïë´╝Ü
ÒÇÇÒÇǵ¡úÕêÖÞí¿Þ¥¥Õ╝ÅÚØ×Õ©©Õ╝║Õñº´╝îõ¢åµÿ»Õ«âÕãêõ©ìÞâ¢õ©║µ»Åõ©Çõ©¬Úù«ÚóÿµÅÉõ¥øµ¡ú╝ï«þÜäÞºúÕå│µûÊÄíêÒÇéõ¢áÕ║öÞ»ÑÕ¡ªõ╣á¡æø_ñƒÕñÜþÜäþƒÑÞ»åÕQîõ╗ÑÞ¥¿Õê½õ╗Çõ╣êµùÂÕÇÖÕ«âõ╗¼µÿ»ÕÉêÚÇéþÜäÕQîõ╗Çõ╣êµùÂÕÇÖÕ«âõ╗¼õ╝ÜÞºúÕå│õ¢áþÜäÚù«ÚóÿÕQîõ╗Çõ╣êµùÂÕÇÖÕ«âõ╗¼õ±öþöƒþÜäÚù«Úóÿµ»öÞªüÞºúÕå│þÜäÚù«ÚóÿÞ┐ÿÞªüÕñÜÒÇ?br>ÒÇÇÒÇÇõ©Çõ║øõØhÕQîÚüçÕê¯C©Çõ©¬Úù«ÚóÿµùÂ׫▒µâ│ÕQ?#8220;µêæþƒÑÚüô´╝îµêæÕ░åõ¢┐þö¿µ¡úÕêÖÞí¿Þ¥¥Õ╝ÅÒÇ?#8221;þÄ░Õ£¿õ╗ûµ£ëõ©ñõ©¬Úù«Úóÿõ║åÒÇéÔÇöÔÇöJamie Zawinski
sdfond 2010-03-12 13:06 ÕÅæÞí¿Þ»äÞ«║
]]>ÒÇÉÚóÿþø«Õêåµ×ÉÒÇ?br>ÒÇÇÒÇÇÕ»╣õ║Äïéïþøÿµö¥Þ×RÚù«ÚóÿÕÅ»õ╗Ñþö¿þ╗äÕÉêµò░Õ¡ªþÜäþƒÑÞ»åµØÑÞºúÕå╗I╝îõ¢åµÿ»Õ»╣õ║ÄÕɽþªüÕî║þÜäµæåµö¥Úù«ÚóÿÕQîÞÖ¢þäÂþ╗äÕÉêµò░Õ¡ªþ╗ÖÕçÌZ║å¥lÅÕà©þÜäµúïþøÿÕñÜÖÕ╣Õ╝Å+Õ«ÊÄûÑÕăþÉåþÜäÞºúµ│ò´╝îõ¢åµÿ»Õ«×ÚÖàõ©¡µúïþøÿÕñÜÖÕ╣Õ╝ÅþÜäµ▒éÞºúµÿ»Õ¥êÕø░ÚÜäíÜäÕQîÕøᵡñõ©ÇÞê¼Ú£ÇÞªüÕǃÕè®þèµÇüÕÄï¥~®Õ迵ÇüÞºäÕêƵ▒éÞºúÒÇ?br>ÒÇÇÒÇÇþÄ░Õ£¿Úóÿþø«õ©¡Þªüµ▒éÕç║õ║Æõ©ìµöıdç╗þÜäÞ▒íþÜäµû╣µ│òµò░ÕQîÞ▒íþÜäµö╗Õç╗ÞÁ\¥U┐µÿ»µû£þÜäÕQîµÿ»õ©ìµÿ»ÕÅ»õ╗ÑÞÇâÞÖæÚççþö¿µö¥Þ×RþÜäµû╣µ│òµØÑÞºúÕæóÕQƒÕ░åïéïþøÿÚ╗æþÖ¢µƒôÞë▓ÕQîÕªéµ×£õ©Çõ©¬Þ▒íÕ£¿Ú╗æÞë▓þÜäµá╝Õ¡ÉÚçîÚØóÕQîÚéúõ╣êÕ«âõ©ÇÕ«Üõ©ìõ╝ܵö╗Õçıdê░þÖ¢Þë▓þÜäµá╝Õ¡É´╝îÿqÖµáÀþÜäÞ»ØÕÅ»õ╗ÑÕêåÕ╝ÇÞ«íµò░ÕQîþäÂÕÉĵ£ÇÕÉÄÕê®þö¿õ╣ÿµ│òÕăþÉåÕèáÞÁõhØÑ׫Ìpíîõ║åÒÇéµèèïéïþøÿµùïÞØ{45Õ║ª´╝îÿqÖµáÀÞ▒íþÜäµöıdç╗ÞÀ»þ║┐׫▒µÿ»þø┤þÜäõ║å´╝îÕªéµ×£ÕŬÞÇâÞÖæõ©Ç┐UìÚó£Þë▓þÜä޻ش╝îÚéúõ╣êÚù«Úóÿ׫ÌpØ{ÕÅÿµêÉõ║åþ╗ÅÕà©þÜäµö¥Þ×RÚù«Úóÿõ║å´╝îÕÅ»õ╗ÑÕê®þö¿Õ迵ÇüÞºäÕêÆÞºúÕåƒÙÇ?br>ÒÇÇÒÇÇÞ«¥dp[i][j]Þí¿þñ║ÕëìiÞíîµö¥õ║åjõ©¬Þ×RþÜäµû╣µ│òµò░ÕQîc[i]Þí¿þñ║¢W¼iÞíîÕÅ»õ╗ѵö¥¥|«þÜäïéïաɵò░ÚçÅÕQîÚéúõ╣êÞØ{┐U└Lû╣¢EïõÏôÕQ?br>ÒÇÇÒÇÇÒÇÇÒÇÇdp[i][j] = dp[i-1][j] + dp[i-1][j-1] * (c[i] - (j - 1))
ÒÇÇÒÇÇÚ£ÇÞªüµ│¿µäÅþÜäµÿ»cµò░þ╗äÕ║ö޻ѵÿ»Õó×Õ║ÅþÜäÕQîÞ┐ÖµáõhëìÞâ¢õ┐ØÞ»üÕëìÚØóþÜäj-1Þíîµö¥õ║åÞ×RÕQîÕ»╣Õ║öÞ┐Öõ©ÇÞíîÕ░▒µ£ëj-1õ©¬õ¢ì¥|«õ©ìÕÅ»µö¥õ║åÒÇ?br>ÒÇÇÒÇÇÿqÖõ©¬Úóÿþø«þÜädpµû╣þ¿ïõ©ìÚÜ¥µâ╗I╝îõ¢åµÿ»Õªéõ¢òµè赿íÕ×ïÞØ{ÕîûÕê░µö¥Þ×RÚù«Úóÿµÿ»õ©ìÕ«ÊÄÿôµâø_ê░þÜä´╝î׫ñÕàµÿ»Õ░åïéïþøÿÚ╗æþÖ¢µƒôÞë▓ÕÉÄÕêåÕ╝ÇÞ«íµò░þÜäµâ│µ│ò´╝îÚØ×Õ©©ÕÀºÕªÖÒÇ?br>
Úóÿþø«õ╗úþáüÕQ?
1 #include <iostream>
2 #include <algorithm>
3 using namespace std;
4 const int N = 70;
5
6 void init(int n, int c1[N], int c2[N])
7 {
8 memset(c1, 0, sizeof(int) * N);
9 memset(c2, 0, sizeof(int) * N);
10 for (int i = 1; i <= n; i++)
11 {
12 for (int j = 1; j <= n; j++)
13 {
14 if ((i + j) & 1)
15 c2[(i+j)/2]++;
16 else
17 c1[(i+j)/2]++;
18 }
19 }
20 }
21 void bishops(int n, int dp[N][N], int c[N])
22 {
23 for (int i = 0; i <= n; i++)
24 dp[i][0] = 1;
25 for (int i = 1; i <= n; i++)
26 for (int j = 1; j <= c[i]; j++)
27 dp[i][j] = dp[i-1][j] + dp[i-1][j-1] * (c[i] - j + 1);
28 }
29
30 int main()
31 {
32 int n, k, c1[N], c2[N], dp1[N][N], dp2[N][N], ans;
33
34 while (scanf("%d %d", &n, &k) == 2)
35 {
36 if (n == 0 && k == 0)
37 break;
38 init(n, c1, c2);
39 sort(c1 + 1, c1 + n + 1);
40 sort(c2 + 1, c2 + n);
41 memset(dp1, 0, sizeof(dp1));
42 memset(dp2, 0, sizeof(dp2));
43 bishops(n, dp1, c1);
44 bishops(n - 1, dp2, c2);
45 ans = 0;
46 for (int i = 0; i <= k; i++)
47 ans += dp1[n][i] * dp2[n-1][k-i];
48 printf("%d\n", ans);
49 }
50
51 return 0;
52 }
2 #include <algorithm>
3 using namespace std;
4 const int N = 70;
5
6 void init(int n, int c1[N], int c2[N])
7 {
8 memset(c1, 0, sizeof(int) * N);
9 memset(c2, 0, sizeof(int) * N);
10 for (int i = 1; i <= n; i++)
11 {
12 for (int j = 1; j <= n; j++)
13 {
14 if ((i + j) & 1)
15 c2[(i+j)/2]++;
16 else
17 c1[(i+j)/2]++;
18 }
19 }
20 }
21 void bishops(int n, int dp[N][N], int c[N])
22 {
23 for (int i = 0; i <= n; i++)
24 dp[i][0] = 1;
25 for (int i = 1; i <= n; i++)
26 for (int j = 1; j <= c[i]; j++)
27 dp[i][j] = dp[i-1][j] + dp[i-1][j-1] * (c[i] - j + 1);
28 }
29
30 int main()
31 {
32 int n, k, c1[N], c2[N], dp1[N][N], dp2[N][N], ans;
33
34 while (scanf("%d %d", &n, &k) == 2)
35 {
36 if (n == 0 && k == 0)
37 break;
38 init(n, c1, c2);
39 sort(c1 + 1, c1 + n + 1);
40 sort(c2 + 1, c2 + n);
41 memset(dp1, 0, sizeof(dp1));
42 memset(dp2, 0, sizeof(dp2));
43 bishops(n, dp1, c1);
44 bishops(n - 1, dp2, c2);
45 ans = 0;
46 for (int i = 0; i <= k; i++)
47 ans += dp1[n][i] * dp2[n-1][k-i];
48 printf("%d\n", ans);
49 }
50
51 return 0;
52 }
µ│¿´╝ܵ£¼µûçõ¢£õ║Ä2009‗q?µ£?3µù?19þé?1Õê?br>
sdfond 2010-02-06 17:58 ÕÅæÞí¿Þ»äÞ«║
]]>ÒÇÉÚóÿþø«Õêåµ×ÉÒÇ?br>ÒÇÇÒÇÇÿqÖõ©¬Úóÿþø«õ╣ìõ©Çþ£ïµî║¢ÄÇÕìòþÜäÕQîõ¢åµÿ»µâ│ÕüÜÕ»╣ÿqÿµÿ»Þªüõ╗ö¥låþÜäµÇØÞÇâõ©ïþÜäÒÇéÞíÑÚøåÞØ{ÕîûþÜäµÇصâ│ÕQîµ▒éÕç║µëǵ£ëÕà▒¥U┐þÜäõ©ëÕàâ¥lä´╝îþäÂÕÉÄþö¿µÇ└Lò░ÕçŵÄë׫▒µÿ»¢{öµíêõ║å´╝îÕà│Úö«×«▒µÿ»Õªéõ¢òµ▒éÕà▒¥U┐õ©ëÕàâþ╗äÒÇéxÕØɵáçþø©ÕÉîÕÆîyÕØɵáçþø©ÕÉîþÜäµ»öÞ¥âÕÑ¢Þ«íþ«ùÕQîÕ£¿õ©ÇµØíµû£¥U┐þÜä׫Îâ©ìÕÑ¢þ«ùõ║å´╝îþöÍM©¬ÕøæÍÅæþÄÄ═╝îÕì│õï╔µû£þÄçþø©ÕÉîþÜäþ║┐ÕQîþ╗ÅÿqçþÜäµá╝þé╣µò░ÕÅ»Þâ¢ÕÉäõ©ìþø©ÕÉîÒÇéµÇØÞÁ\Õ¢ôþäÂÿqÿµÿ»µ×ÜõïDy / xÕQêõ©ìÕÉîþÜäy / x╝ï«Õ«Üõ║åõ©ìÕÉîþÜäþƒ®Õ┼×Õî║ÕƒƒÕQë´╝îõ╣ïÕÉÄÕªéõ¢òµ£ëµòêþÜäÞ«í¢Äù´╝îµêæÚççþö¿þÜäµûÊÄ│òÕÅ»Þ⢵£ëõ║øÚ║╚ØâªÕQîµ£ëþé╣þ▒╗Õ«ÊÄûÑþÜäµû╣µ│òÒÇéõ╗ѵû£þÄçõ©║a / bõ©ÌZ¥ïÕQ?a, b) = gÕQîÚéúõ╣êm * nþÜäÕî║ÕƒƒÕåàõ©Çիܵ£ë(m - a + 1) * (n - b + 1)õ©¬Úéúõ╣êÕñºþÜäþƒ®Õ¢ó´╝îÿqÖµáÀþÜäþƒ®Õ¢óþ╗ÅÿqçþÜäµá╝þé╣µò░µÿ»(g + 1)ÕQøþäÂÕÉÄÕøáõ©║ÕÉî¢{ëµû£þÄçÕ░Åõ©Çþé╣þÜäþƒ®Õ┼×(a - a / g, b - b / g)õ╣ƒµÿ»Õ¡ÿÕ£¿þÜä´╝îõ©¬µò░ÕÉîµáÀÕÅ»õ╗Ñ¥lƒÞ«íÕç║µØÑÕQîõ¢åµÿ»µ£ëõ║øÕñºþƒ®Õ┼×Õîàµï¼õ║å´╝îÞªüÕÄ╗µÄë´╝øÕøᵡñ׫▒Úççþö¿Þ┐Ö┐UìµÇصâ│ÕQîÕàêµ▒éÕç║Õñºþƒ®Õ¢óþÜäõ©¬µò░ÕQîþäÂÕÉÄõ¥ØïãíÕ¥Çõ©ïÕçÅÕQîÕ░▒ÕÅ»õ╗ÑÚü┐ÕàìÚçìÕñìÞ«íµò░õ║åÒÇéÞÖ¢þäÂÞ┐ÖµáÀÕñìµØéÕ║ªµ£ëþé╣Ú½ÿ´╝îõ©ìÞ┐çµ×üÚÖɵò░µì«ÿqÿµÿ»µ»öÞ¥âÕ┐½þÜäÞÀæÕç║µØÑõ║åÒÇ?br>ÒÇÇÒÇÇÞ»┤þÜäÕÅ»Þâ¢õ©ìÕñ¬µ©àµÑÜÕQîÕàÀõ¢ôõ╗úþáüÕªéõ©ï´╝Ü
1 #include <cstdio>
2 #include <iostream>
3 using namespace std;
4 const int N = 1024;
5
6 bool tag[N][N];
7 long long calc(long long n)
8 {
9 if (n <= 2)
10 return 0;
11 return n * (n - 1) * (n - 2) / 6;
12 }
13 int gcd(int a, int b)
14 {
15 return b == 0 ? a : gcd(b, a % b);
16 }
17
18 int main()
19 {
20 int m, n, g, a, b, timer = 1, cnt[N], ta, tb;
21 long long ans;
22
23 while (scanf("%d %d", &m, &n) == 2)
24 {
25 memset(tag, 0, sizeof(tag));
26 if (m == 0 && n == 0)
27 break;
28 ans = calc((m + 1) * (n + 1)) - calc(m + 1) * (n + 1) - calc(n + 1) * (m + 1);
29 for (int i = m; i >= 1; i--)
30 for (int j = n; j >= 1; j--)
31 {
32 g = gcd(i, j);
33 a = i / g, b = j / g;
34 if (tag[a][b]) continue;
35 memset(cnt, 0, sizeof(cnt));
36 tag[a][b] = 1;
37 a = i, b = j;
38 ta = i / g, tb = j / g;
39 for (int k = g; k >= 2; k--)
40 {
41 cnt[k] += (m - a + 1) * (n - b + 1);
42 ans -= calc(k + 1) * cnt[k] * 2;
43 for (int t = 1; t <= k - 2; t++)
44 cnt[k-t] -= (t + 1) * cnt[k];
45 a -= ta, b -= tb;
46 }
47 }
48 cout << "Case " << timer++ << ": " << ans << endl;
49 }
50
51 return 0;
52 }
53
2 #include <iostream>
3 using namespace std;
4 const int N = 1024;
5
6 bool tag[N][N];
7 long long calc(long long n)
8 {
9 if (n <= 2)
10 return 0;
11 return n * (n - 1) * (n - 2) / 6;
12 }
13 int gcd(int a, int b)
14 {
15 return b == 0 ? a : gcd(b, a % b);
16 }
17
18 int main()
19 {
20 int m, n, g, a, b, timer = 1, cnt[N], ta, tb;
21 long long ans;
22
23 while (scanf("%d %d", &m, &n) == 2)
24 {
25 memset(tag, 0, sizeof(tag));
26 if (m == 0 && n == 0)
27 break;
28 ans = calc((m + 1) * (n + 1)) - calc(m + 1) * (n + 1) - calc(n + 1) * (m + 1);
29 for (int i = m; i >= 1; i--)
30 for (int j = n; j >= 1; j--)
31 {
32 g = gcd(i, j);
33 a = i / g, b = j / g;
34 if (tag[a][b]) continue;
35 memset(cnt, 0, sizeof(cnt));
36 tag[a][b] = 1;
37 a = i, b = j;
38 ta = i / g, tb = j / g;
39 for (int k = g; k >= 2; k--)
40 {
41 cnt[k] += (m - a + 1) * (n - b + 1);
42 ans -= calc(k + 1) * cnt[k] * 2;
43 for (int t = 1; t <= k - 2; t++)
44 cnt[k-t] -= (t + 1) * cnt[k];
45 a -= ta, b -= tb;
46 }
47 }
48 cout << "Case " << timer++ << ": " << ans << endl;
49 }
50
51 return 0;
52 }
53
sdfond 2009-10-15 19:54 ÕÅæÞí¿Þ»äÞ«║
]]>ÒÇÇÒÇÇõ╣ƒÕ░▒µÿ»õ©Çõ©¬Õ«╣µûÑÕăþÉåÒÇéþäÂÕÉĵÇ╚ØÜäµ£ƒµ£øE = sigma{C(n, i) * P(i) * i * n * d}ÕQîi = 0 ... NÒÇ?br>ÒÇÇÒÇÇÿqÖõ©¬Õ╝ÅÕ¡ÉÕêùÕç║µØÑÕÉĵÇÄõ╣êõ╣ƒµ▒éõ©ìÕç║¥lôµ×£ÒÇéµÖÜõ©èimemsÕæèÞ»ëõ║åµêæõ©Çõ©¬Õ¥ê¢ÄÇÕìòþÜäµÄ¿Õ»╝µûÊÄ│òÒÇéÕ»╣õ║Äõ©Çõ©¬ÕòåÕ║ùµØÑÞ»▀_╝îõ©Çõ©¬õØhõ©ìÕÄ╗þÜ䵪éþÄçµÿ»(N - 1) / NÕQîÚéúõ╣êMõ©¬õØhÚâ¢õ©ìÕÄ╚ØÜ䵪éþÄçµÿ?(N - 1) / N) ^ MÕQîþö¿1ÕçÅÕÄ╗ÿqÖõ©¬¥lôµ×£×«▒µÿ»Þé»Õ«ÜÞçø_░æµ£ëõØhÕÄ╗Þ┐Öõ©¬ÕòåÕ║ùþÜ䵪éþÄçÒÇéþäÂÕÉĵÇ╚ØÜäµ£ƒµ£ø׫Îâ╣ÿõ╗ÑNõ©¬ÕòåÕ║ù´╝îÕåìõ╣ÿõ╗ÑÞÁÜÚÆ▒µò░n * d׫▒ÕÅ»õ╗Ñõ║åÒÇéÕ¥êÕÀºÕªÖÕQîÕøáõ©ÌZ╗ûµÿ»õ╗ÄÕòåÕ║ùþÜäÞºÆÕ║ªþø┤µÄÑÞÇâÞÖæþÜäÚù«Úóÿ´╝îÞÇîõ©ìÞÇâÞÖæÕòåÕ║ùþÜäõØhµòÄ═╝îÿqÖµáÀ׫Îâ©ìþö¿ÕêùµªéþÄçÕêåÕ©âõ║åÒÇ?br>ÒÇÇÒÇÇõ¢åµÿ»õ©èÚØóþÜäÕà¼Õ╝ÅÕ░▒õ©ìÞ⢵Ŀջ╝Õç║µ¡ú╝ï«þ╗ôµ×£õ║åõ╣ê´╝îÕÉĵØÑÕÅêµÄ¿õ║åõ©Çõ©ï´╝îÕÅæþÄ░µÿ»ÕÅ»õ╗ÑþÜäÕQêþàºþØÇ¥lôµ×£þî? -!ÕQëÒÇ?br>ÒÇÇÒÇÇÕàÀõ¢ôþÜäµÄ¿Õ»╝Õ¥êÚ║╚ØâªÕQîõ¢åµÿ»µÇ╚ØÜäµØÑÞ»┤þö¿Õê░õ║åþ╗äÕÉêµò░Õ¡ªþÜäÕçáõ©¬Õà¼Õ╝ÅÒÇéÚªûÕà?nbsp;k * C(n, k) = n * C(n - 1, k - 1)ÕQîÕê®þö¿Þ┐Öõ©¬Õà¼Õ╝ŵèèÕñûÚØóþÜäiµÂêÕÄ╗ÒÇéþäÂÕÉĵ£ëpascalÚÇƵĿÕ╝Å´╝ÜC(n, k) = C(n - 1, k) + C(n - 1, k - 1)ÒÇéµêæõ╗¼ÕêåÕê½ÞÇâÞÖæ(i / N) ^ MÕëìÚØóþÜäþ│╗µòÄ═╝îÕÅ»õ╗ÑÕÅæþÄ░Ú⢵ÿ»õ©ñõ©¬õ║îÚí╣Õ╝Åþ│╗µò░þø©õ╣ÿþÜäµû╣Õ╝ÅÒÇéµèèÕàÂõ©¡þÜäõ©Çõ©¬Õê®þö¿pascalÕà¼Õ╝ÅÕ▒òÕ╝ÇÕÉÄ´╝îÕç║þÄ░õ║åÕ┼×ÕªéC(n, 0) - C(n, 1) + C(n, 2) - ...õ╣ïþ▒╗þÜäÕ╝ÅÕ¡É´╝î¥lôµ×£µÿ?ÕQîµÂêÕÄÍM║åÒÇéÕë®õ©ïþÜäÿqÿµÿ»õ©ñõ©¬õ║îÚí╣Õ╝Åþ│╗µò░þÜäõ╣ÿþº»ÕQîõ©ìÿqçÚ⢵ÿ»Þ┐Ö┐UìÕ┼×Õ╝ÅþÜäÕQÜC(n, k) * C(k, r)ÕQîÕ«â¢{ëõ║ÄC(n, r) * C(n - 1, k - 1)ÒÇéÞ┐ÖµáÀÕÅÿÕ¢óõ╣ïÕÉĵ£ëõ©Çõ©¬Õà¼Õà▒Úí╣׫▒ÕÅ»õ╗ѵÅÉÕç║ÕÄ╗õ║å´╝îÚçîÚØóÿqÿµÿ»Õ¢óÕªé(1 - 1) ^ nþÜäÕ┼×Õ╝ÅÒÇéÞ┐Öµá´L╗ôµ×£Õ░▒µÿ?ÒÇéÕ£¿Þ«íþ«ùõ©ïõ©ÇÖÕ╣þÜä¥p└Lò░þÜäµùÂÕÇÖ´╝î¢W¼õ©ÇïãíÕ▒òÕ╝ÇÕÉÄÚçîÚØóµü░ÕÑ¢ÕîàÕɽõ║åÕëìõ©ÇÖÕ╣þÜä¥p└Lò░ÕQîþø┤µÄÑÕ░▒µÿ?µÂêÕÄ╗õ║å´╝îþäÂÕÉÄ¥lºþ«ïÕê®þö¿õ©èÚØóþÜäµû╣µ│òÕ▒òÕ╝ÇÒÇéõ©¡Úù┤µÄ¿Õ»╝þÜäÿqçþ¿ïõ©¡Þ┐ÿÚ£ÇÞªüµÀ╗Õèáõ©Çõ║øÕÇÚgÏô0þÜäÚí╣õ¥┐õ║Ä¥lºþ«ïþÜäµÄ¿Õ»╣{Ç?br>ÒÇÇÒÇÇÿqÖõ©¬µûÊÄ│òÕ¥êÚ║╗þ⪴╝îõ©ìÞ┐çµÄ¿Õ»╝ÿqçþ¿ïõ©¡Þ┐ÿµÿ»þö¿Õê¯C║åÕ¥êÕñÜþƒÑÞ»åþÜä´╝î׫▒Õ¢ôÕñìõ╣áõ║? -!ÕàÂÕ«×ÿqÖõ©¬µÄ¿Õ»╝Þªüõ©ìµÿ»þƒÑÚüôõ║åµ£ÇÕÉÄþÜäÕà¼Õ╝Åõ╣ƒõ©ìµòóµÄ¿ÕQîÕ«×Õ£¿Õñ¬Ú║╚ØâªÕQîþ£ïµØÑÞ┐ÿµÿ»Õƒ║µ£¼Õèƒïãáþ╝║Õòè´╝îÞÇîõ©ö¢ÄùµªéþÄçþÜäÚóÿþø«ÿqÿµÿ»ÞªüÕñÜ¥lâõ╣á¥lâõ╣áÒÇéÕŪÕñûµ│¿µäŵÇØþ╗┤þÜäþüÁïz└LǺ´╝îÕàÂÕ«×¢ÄÇÕìòÕüܵ│òõ©ìÚÜ¥µâ│ÕQîõ¢åµÿ»µ£ÇÕ╝ÇÕºïÞó½ÕÉëÕñºþëøÞ»»Õ»Úg║åÕQîÕ░▒þö¿õ║åõ©Çõ©¬õ©Ñµá╝þÜäµÄ¿Õ»╝µûÊÄ│òÕQîþï¼þ½ïµÇØÞÇâÞ┐ÿµÿ»Õ¥êÚçìÞªüþÜäÒÇ?br>
Úóÿþø«õ╗úþáüÕQ?br>
1 #include <cstdio>
2 #include <cmath>
3
4 int main()
5 {
6 double N, M, n, d;
7
8 while (scanf("%lf %lf %lf %lf", &N, &M, &n, &d) == 4)
9 printf("%.3lf\n", n * d * N * (1.0 - pow(1.0 - 1.0 / N, M)));
10
11 return 0;
12 }
13
2 #include <cmath>
3
4 int main()
5 {
6 double N, M, n, d;
7
8 while (scanf("%lf %lf %lf %lf", &N, &M, &n, &d) == 4)
9 printf("%.3lf\n", n * d * N * (1.0 - pow(1.0 - 1.0 / N, M)));
10
11 return 0;
12 }
13
sdfond 2009-06-18 21:48 ÕÅæÞí¿Þ»äÞ«║
]]>ÒÇÉþ«ùµ│òÕêåµ×ÉÒÇ?br>ÒÇÇÒÇǵäƒÞºëµ╗íµüÂÕ┐âþÜäõ©Çõ©¬Úóÿþø«´╝îÚ£ÇÞªüþû»þïéþÜäµë¥ÞºäÕ¥ïÒÇéÚªûÕàêÕ«╣µÿôþ£ïÕç°ÖÁ\Õ¥äµò░µÿ»õ©Çõ©¬þ╗äÕÉêµò░ÕQîÕãêõ©öµ»Åõ©ÇÕ▒éÚ⢵ÿ»µ¿íÕà¡Õ¾@þÄ»þÜäÒÇéõ¢åµÿ»µÇĵáÀµëæÍê░Õ▒éµò░ÕQêõ╣ƒ×«▒µÿ»µ£Çþƒ¡ÞÁ\Õ¥äÚò┐Õ║ª´╝ëÕæó´╝ƒµ£ÇÕ╝ÇÕºïµâ│Õ╗║þ½ïÕØɵáç¥p╚ØäÂÕÉÄÕê®þö¿Õçáõ¢òµû╣µ│òþ«ùÕç║µØÑÕQîõ¢åµÿ»Õªéõ¢òµùáÞ«║µÿ»¢WøÕìí׫öÕØɵáçþ│╗ÿqÿµÿ»µ×üÕØɵáçþ│╗þÜäÕ¥Åþ½ïÚ⢵ÿ»Õø░ÚÜäíÜäÕQøþäÂÕÉĵâ│Õ¡ÿÕø¥‗q┐µÉ£ÕQîÕÅæþÄ░þ®║Úù┤õ©ìÕñƒÒÇéÕÉĵØÑÕÅæþÄÄ═╝îµèèÕø¥ÖÕ║µùÂÚÆêÞØ{90Õ║ª´╝îÕç║þÄ░õ║åõ©Çõ©¬Õ¥êµ£ëµäŵÇØþÜäÞºäÕ¥ïÒÇéõ╗ÑÕăþé╣ÕQêµò░Õ¡ùõÏô1ÕQëõÏôõ©¡Õ┐âÕ╗║þ½ïÕØɵáç¥p╗´╝îõ©ìÞ┐çÕØɵáçþÜäÚÇëÕÅûÚ£ÇÞªüõ©Çõ║øµèÇÕÀºÒÇéÕÅ»õ╗Ñþ£ïÕç║µò░Õ¡ùµÿ»õ©ÇÕ▒éÕ▒éÕêåÕ©âþÜä´╝îÕÅûxÕÀªÞ¥╣þÜäþé╣ÕØɵáçõ©║´╝ê-2ÕQ?ÕQë´╝îõ╗ÑÕÉĵ»ÅÕ¥ÇÕÀªÕó×Õèáõ©ÇÕ▒é´╝¬ÕØɵáçÕ░▒ÕÅÿÕîû2ÒÇéÕàÂÕ«×ÕÆîÕăþé╣¥UÁÕØɵáçþø©ÕÉîõ©öõ¢ìõ║ÄÕàÂÕÀªÞ¥╣þÜäþéÊÄü░ÕÑ¢µÿ»µ»Åõ©ÇÕ▒éµò░Õ¡ùµ£ÇÕñºþÜä¥lôþé╣ÕQüÞ┐ÖµáÀÕŬުüþí«Õ«Üõ║åÿqÖõ©¬þé╣´╝îÕÅ»õ╗ѵîëþàºÚÇåµùÂÚÆêþÜäÖÕ║Õ║Åõ¥Øµ¼í¥lÖÞ┐Öõ©ÇÕ▒éþÜäµëǵ£ëþé╣þÜäÕØɵáçµÄ¿Õç║µØÑÒÇéÞ┐Öµá°P╝î¥lÖÕ«Üõ©Çõ©¬µò░Õ¡ù´╝îµêæõ╗¼ÕÅ»õ╗ѵáÊÄ쫵»Åõ©ÇÕ▒éµ£ÇÕñºþÜäµò░Õ¡ùµÄ¿Õç║ÿqÖõ©¬µò░þÜäÕØɵáçÒÇ?br>ÒÇÇÒÇÇþÄ░Õ£¿µ£ëõ║åÕØɵáçÕQêÕÅ»õ╗Ñþ£ïµêɵÿ»µø╝ÕôêÖÕ┐ÕØɵáç´╝ëÕQîÕ░▒ÕÅ»õ╗ѵĿµÁïÞÀ»Õ¥äõ║åÒÇéµèèõ©ñõ©¬µò░Õ¡ùþÜäÕØɵáçµ▒éÕÀ«´╝î׫▒ÕÅ»õ╗Ñþ£ïµêɵÿ»õ©Çõ©¬Õ£¿Õăþé╣õ║åÒÇéÕØɵáçÕÆîÞÀ»Õ¥äþÜäÕà│¥pÍM©ìµÿ»Õ¥êÕÑ¢µë¥ÕQîÕåÖõ║?ÒÇ?ÞíîÕÅæþįC║åõ©Çõ©¬Õ¥êÞ»íÕ╝éþÜäÞºäÕ¥ïÒÇéÕàêµèèÕØɵáçÕîûµêɵ¡úþÜä´╝îþäÂÕÉÄÕÅæþÄ░x >= yþÜäµùÂÕÇÖÕ░▒µÿ»C( (x + y) / 2, y)ÕQîÕɪÕêÖµÿ»C( y, (y - x) / 2)ÒÇéõ╣ïÕÉÄÕ░▒µÿ»Ú½ÿ¥_æÍ║ªõ║åÒÇ?br>
Úóÿþø«õ╗úþáüÕQ?br>
1 import java.util.*;
2 import java.math.*;
3
4 class point
5 {
6 int x, y;
7 public point(int x, int y)
8 {
9 this.x = x;
10 this.y = y;
11 }
12 }
13 class Main
14 {
15 public static void main(String[] args)
16 {
17 Scanner in = new Scanner(System.in);
18 int a, b, len;
19 BigInteger ans;
20 point pa, pb;
21
22 while (in.hasNext())
23 {
24 a = in.nextInt();
25 b = in.nextInt();
26 if (a == 0 && b == 0)
27 break;
28 pa = GetCoordinate(a);
29 pb = GetCoordinate(b);
30 pa.x = pb.x - pa.x;
31 pa.y = pb.y - pa.y;
32 pa.x = pa.x < 0 ? -pa.x : pa.x;
33 pa.y = pa.y < 0 ? -pa.y : pa.y;
34 if (pa.x >= pa.y)
35 {
36 len = (pa.x + pa.y) / 2;
37 ans = C(len, pa.y);
38 }
39 else
40 {
41 len = pa.y;
42 ans = C(len, (pa.y - pa.x) / 2);
43 }
44 System.out.print("There ");
45 if (ans.compareTo(BigInteger.ONE) == 0)
46 System.out.print("is 1 route");
47 else
48 System.out.print("are " + ans + " routes");
49 System.out.println(" of the shortest length " + len + ".");
50 }
51 }
52 static BigInteger C(int n, int k)
53 {
54 BigInteger ret = BigInteger.ONE;
55 if (k > n - k)
56 k = n - k;
57 for (int i = 1; i <= k; i++)
58 {
59 ret = ret.multiply(new BigInteger(new String(n - i + 1 + "")));
60 ret = ret.divide(new BigInteger(new String(i + "")));
61 }
62 return ret;
63 }
64 static point GetCoordinate(int n)
65 {
66 int[][] dir = new int[][]{{1, -1}, {2, 0}, {1, 1}, {-1, 1}, {-2, 0}, {-1, -1}};
67 int i = 0, j = 0, k = 0, tx, ty, cnt = 0, delta;
68 point p = new point(0, 0);
69
70 if (n == 1)
71 return p;
72 for (i = 2; i <= 1000; i++)
73 if ((3 * i * i - 3 * i + 1) >= n)
74 break;
75 delta = 3 * i * i - 3 * i + 1 - n;
76 i--;
77 tx = -2 * i;
78 ty = 0;
79 boolean flag = false;
80 for (j = 0; j < 6; j++)
81 {
82 for (k = 0; k < i; k++)
83 {
84 if (cnt == delta)
85 {
86 flag = true;
87 break;
88 }
89 cnt++;
90 tx += dir[j][0];
91 ty += dir[j][1];
92 }
93 if (flag)
94 break;
95 }
96 p.x = tx;
97 p.y = ty;
98
99 return p;
100 }
101 }
102
2 import java.math.*;
3
4 class point
5 {
6 int x, y;
7 public point(int x, int y)
8 {
9 this.x = x;
10 this.y = y;
11 }
12 }
13 class Main
14 {
15 public static void main(String[] args)
16 {
17 Scanner in = new Scanner(System.in);
18 int a, b, len;
19 BigInteger ans;
20 point pa, pb;
21
22 while (in.hasNext())
23 {
24 a = in.nextInt();
25 b = in.nextInt();
26 if (a == 0 && b == 0)
27 break;
28 pa = GetCoordinate(a);
29 pb = GetCoordinate(b);
30 pa.x = pb.x - pa.x;
31 pa.y = pb.y - pa.y;
32 pa.x = pa.x < 0 ? -pa.x : pa.x;
33 pa.y = pa.y < 0 ? -pa.y : pa.y;
34 if (pa.x >= pa.y)
35 {
36 len = (pa.x + pa.y) / 2;
37 ans = C(len, pa.y);
38 }
39 else
40 {
41 len = pa.y;
42 ans = C(len, (pa.y - pa.x) / 2);
43 }
44 System.out.print("There ");
45 if (ans.compareTo(BigInteger.ONE) == 0)
46 System.out.print("is 1 route");
47 else
48 System.out.print("are " + ans + " routes");
49 System.out.println(" of the shortest length " + len + ".");
50 }
51 }
52 static BigInteger C(int n, int k)
53 {
54 BigInteger ret = BigInteger.ONE;
55 if (k > n - k)
56 k = n - k;
57 for (int i = 1; i <= k; i++)
58 {
59 ret = ret.multiply(new BigInteger(new String(n - i + 1 + "")));
60 ret = ret.divide(new BigInteger(new String(i + "")));
61 }
62 return ret;
63 }
64 static point GetCoordinate(int n)
65 {
66 int[][] dir = new int[][]{{1, -1}, {2, 0}, {1, 1}, {-1, 1}, {-2, 0}, {-1, -1}};
67 int i = 0, j = 0, k = 0, tx, ty, cnt = 0, delta;
68 point p = new point(0, 0);
69
70 if (n == 1)
71 return p;
72 for (i = 2; i <= 1000; i++)
73 if ((3 * i * i - 3 * i + 1) >= n)
74 break;
75 delta = 3 * i * i - 3 * i + 1 - n;
76 i--;
77 tx = -2 * i;
78 ty = 0;
79 boolean flag = false;
80 for (j = 0; j < 6; j++)
81 {
82 for (k = 0; k < i; k++)
83 {
84 if (cnt == delta)
85 {
86 flag = true;
87 break;
88 }
89 cnt++;
90 tx += dir[j][0];
91 ty += dir[j][1];
92 }
93 if (flag)
94 break;
95 }
96 p.x = tx;
97 p.y = ty;
98
99 return p;
100 }
101 }
102
sdfond 2009-06-16 22:12 ÕÅæÞí¿Þ»äÞ«║
]]>#include <cstdio>
const int N = 10010;
int main()
{
int a[N], n, mod[N] = {0}, tmp = 0, len = 0, pos;
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
if (len) continue;
tmp = (tmp + a[i]) % n;
if (tmp == 0)
{
len = i;
pos = 1;
}
if (mod[tmp])
{
len = i - mod[tmp];
pos = mod[tmp] + 1;
}
else
mod[tmp] = i;
}
printf("%d\n", len);
for (int i = 0; i < len; i++)
printf("%d\n", a[pos+i]);
return 0;
}
const int N = 10010;
int main()
{
int a[N], n, mod[N] = {0}, tmp = 0, len = 0, pos;
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
if (len) continue;
tmp = (tmp + a[i]) % n;
if (tmp == 0)
{
len = i;
pos = 1;
}
if (mod[tmp])
{
len = i - mod[tmp];
pos = mod[tmp] + 1;
}
else
mod[tmp] = i;
}
printf("%d\n", len);
for (int i = 0; i < len; i++)
printf("%d\n", a[pos+i]);
return 0;
}
sdfond 2009-06-12 09:09 ÕÅæÞí¿Þ»äÞ«║
]]> 1 #include <cstdio>
2 const int N = 12;
3
4 int p[N], ans;
5 long long gcd(long long a, long long b)
6 {
7 return b == 0 ? a : gcd(b, a % b);
8 }
9 void calc_sg(long long tol, int m, int dep, long long v, bool mark)
10 {
11 if (dep == m)
12 {
13 if (mark) ans -= tol / v;
14 else ans += tol / v;
15 return;
16 }
17 calc_sg(tol, m, dep + 1, v, mark);
18 if (v <= tol)
19 calc_sg(tol, m, dep + 1, v / gcd(v, p[dep]) * p[dep], mark ^ 1);
20 }
21
22 int main()
23 {
24 int T, m, n, a, g;
25
26 scanf("%d", &T);
27 while (T--)
28 {
29 g = 0;
30 bool mark = 1;
31 scanf("%d %d", &m, &n);
32 for (int i = 0; i < m; i++)
33 scanf("%d", &p[i]);
34 for (int i = 0; i < n; i++)
35 {
36 scanf("%d", &a);
37 if (!mark) continue;
38 ans = 0;
39 calc_sg(a, m, 0, 1, 0);
40 g ^= ans;
41 for (int j = 0; j < m; j++)
42 if (a % p[j] == 0)
43 {
44 mark = 0;
45 break;
46 }
47 }
48 if (!mark) puts("Xiao Hong");
49 else printf("%s\n", g ? "Xiao Hong" : "Xiao Gang");
50 }
51
52 return 0;
53 }
54
2 const int N = 12;
3
4 int p[N], ans;
5 long long gcd(long long a, long long b)
6 {
7 return b == 0 ? a : gcd(b, a % b);
8 }
9 void calc_sg(long long tol, int m, int dep, long long v, bool mark)
10 {
11 if (dep == m)
12 {
13 if (mark) ans -= tol / v;
14 else ans += tol / v;
15 return;
16 }
17 calc_sg(tol, m, dep + 1, v, mark);
18 if (v <= tol)
19 calc_sg(tol, m, dep + 1, v / gcd(v, p[dep]) * p[dep], mark ^ 1);
20 }
21
22 int main()
23 {
24 int T, m, n, a, g;
25
26 scanf("%d", &T);
27 while (T--)
28 {
29 g = 0;
30 bool mark = 1;
31 scanf("%d %d", &m, &n);
32 for (int i = 0; i < m; i++)
33 scanf("%d", &p[i]);
34 for (int i = 0; i < n; i++)
35 {
36 scanf("%d", &a);
37 if (!mark) continue;
38 ans = 0;
39 calc_sg(a, m, 0, 1, 0);
40 g ^= ans;
41 for (int j = 0; j < m; j++)
42 if (a % p[j] == 0)
43 {
44 mark = 0;
45 break;
46 }
47 }
48 if (!mark) puts("Xiao Hong");
49 else printf("%s\n", g ? "Xiao Hong" : "Xiao Gang");
50 }
51
52 return 0;
53 }
54
sdfond 2009-06-02 16:01 ÕÅæÞí¿Þ»äÞ«║
]]>polyaÚóÿþø«ÕQ?br>HOJ 2084 The Colored Cubes
HOJ 2647 Megaminx
POJ 1286 Necklace of Beads
POJ 2409 Let it Bead
TOJ 2795 The Queen's New Necklaces
HDU 1812 Count the Tetris
UVa 11255 Necklace
POJ 2154 Color
POJ 2888 Magic Bracelet
UVa 10601 Cubes
NUAA 1110
sdfond 2009-05-12 11:20 ÕÅæÞí¿Þ»äÞ«║
]]>ÕàÂõ©¡A =(Ak-1 Ak-2 ... A1)ÕQîIµÿ»Õìòõ¢ìþƒ®Úÿ³cÇ?br>þäÂÕÉĵ×äÚÇáõ©Çõ©¬k * 1ÕêùÕÉæÚçÅbÕQ?br>
ÿqÖµáÀÕQîM * bõ╣ïÕÉÄb0þÜäÕÇ╝Õ░▒µÿ»f(k)ÕQîõ╗ѵ¡ñþ▒╗µÄ¿´╝îM ^ n * bõ╣ïÕÉÄb0þÜäÕÇ╝Õ░▒µÿ»f(k-1+n)ÕQîþ«ùµ│òÕñìµØéÕ║ªO(k ^ 3 * logn)ÒÇ?br>
sdfond 2009-05-08 22:08 ÕÅæÞí¿Þ»äÞ«║
]]>1.µÄÆÕêù¥läÕÉêõ©ÄÕ«╣µûÑÕăþÉ?br>µÄÆÕêù¥läÕÉêÚçîÚØóþÜ?õ©¬ÚçìÞªüþÜäÕƒ║µ£¼ÕăþÉåÕQÜÕèáµ│òÕăþÉåÒÇüõ╣ÿµ│òÕăþÉåÒÇüÕçŵ│òÕăþÉåÒÇüÚÖñµ│òÕăþÉ?br>ÕëìÚØóõ©ñõ©¬µ£Çõ©║Õƒ║µ£¼´╝îÕÉÄÚØóõ©ñõ©¬µÿ»µá╣µì«Õëìõ©ñõ©¬ïzäíöƒÕç║µØÑþÜäÒÇéõ╣ÿµ│òÕăþÉåµ£ëþÜäµùÂÕÇÖþÜäÕ║öþö¿Õ¥êÕÚyÕªÖ´╝îÕÅ»õ╗Ñõ¢£õÏôõ©Ç┐UìµëôÕ╝ǵÇØÞÁ\þÜäÕè×µ│òÒÇ?br>Õƒ║µ£¼þÜäµÄÆÕêùþ╗äÕÉêõ╣ïÕÉÄ´╝îµÄÑõ©ïµØÑÕ╝òÕçÌZ║åÕñÜÚçìÚøåÒÇéÕñÜÚçìÚøåþÜäµÄÆÕêùþ╗äÕÉêµÿ»õ©Çõ©¬Õ¥ê¥lÅÕà©þÜäÚù«Úóÿ´╝îµÇ╚Ø╗ôÕªéõ©ïÕQ?br>ÕñÜÚçìÚøåþÜäµÄÆÕêùÕQ?br>ÒÇÇÒÇÇÕ࿵ÄÆÕêùþÜäÞ»ØÕŬڣÇÕ║öþö¿ÚÖñµ│òÕăþÉå׫▒ÕÅ»õ╗Ñõ║åÒÇénõ©¬Õàâþ┤áþÜäÕñÜÚçìÚøåþÜärµÄÆÕêùÚ£ÇÞªüÕê®þö¿µîçµò░þöƒµêÉÕ碵ò░µØÑÕüÜÒÇ?br>ÕñÜÚçìÚøåþÜä¥läÕÉêÕQ?br>ÒÇÇÒÇÇnõ©¬Õàâþ┤áþÜäÕñÜÚçìÚøåþÜär¥läÕÉêÕQîÕªéµ×£r׫Åõ║Ä¢{ëõ║Äõ╗ÍM¢òõ©Çõ©¬Õàâþ┤áÕÅ»ÚÇëþÜäõ©¬µò░ÕQîÚéúõ╣êÕ░▒Õ¢Æþ╗ôõ©║þ╗ÅÕà©þÜäõ©ìիܵû╣þ¿ïþÜäÞºúµò░Úù«Úóÿ´╝îÕÅ»õ╗ÑÕê®þö¿“ÚÜöµØ┐µ│?#8221;µØÑÕüÜÒÇéþ╗ôµ×£Õ░▒µÿ»õ©Çõ©¬þ╗äÕÉêµò░ÒÇéÕªéµ×£rÕñºõ║ĵƒÉõ║øÕàâþ┤áþÜäÕÅ»ÚÇëõ©¬µòÄ═╝îÚéúõ╣êõ©Ç┐Uìµû╣µ│òµÿ»Õê®þö¿Õ«ÊÄûÑÕăþÉåÕQîõ©Ç┐Uìµû╣µ│òÞ┐ÿµÿ»Þªüõ¥ØÚØáþöƒµêÉÕ碵ò░ÕQêþ╝û¢EïÕ║ÅþÜäµùÂÕÇÖÕÅ»õ╗Ñþö¿Õè¿Õ¢ÆÕüÜ´╝ëÒÇ?br>Õªéµ×£µÿ»õ©Çõ©¬þĻբóþÜäµÄÆÕêù¥läÕÉêÕQîÚéúõ╣êÚù«ÚóÿÕ░▒Õø░ÚÜ¥Þ«©ÕñÜÕQîÞªüÕê®þö¿¥|«µìó¥ƒñÕÆîpolyaÕ«ÜþÉåÒÇ?br>ÒÇÇÒÇÇÕìòþ║»þÜäõ¥ØÚØáÕøøÖÕ╣Õƒ║µ£¼ÕăþÉåµØÑÞ«íµò░ÕQîµ£ëþÜäµùÂÕÇÖõ╝ܵÿæÍ¥ùÕèøõ©ìõ╗ÄÕ┐âÕQîÞ┐Öõ©¬µùÂÕÇÖÕ░▒Ú£ÇÞªüÕ«╣µûÑÕăþÉåþÜäÕ©«Õè®ÒÇéÕ«╣µûÑÕăþÉåþë╣Õê½ÚÇéÕÉêÞºúÕå│ÞïÑÕ╣▓ÚÖÉÕêµØíõÜgþÜäõ║ñÒÇüÕãêÚù«ÚóÿÕQîõ╣ƒµÿ»µëôÕ╝ǵÇØÞÁ\þÜäõ©Ç┐Uìµû╣µ│òÒÇ?br>ÒÇÇÒÇÇÕê®þö¿Õ«ÊÄûÑÕăþÉåÞºúÕå│þÜäþ╗ÅÕàöRù«Úóÿµ£ëÕQÜÚöÖµÄÆÚù«Úóÿ´╝îÕ©ªþªüµ¡óõ¢ì¥|«þÜäµÄÆÕêùÒÇéþªüõ¢ìµÄÆÕêùµÇ╗ÞºëÕ¥ùþö¿Õ«ÊÄûÑÕăþÉåÞºúÕå│þÜäõ©ìÕñƒõ╝ÿ¥ƒÄ´╝îõ©ìþƒÑÚüôµ£ëµ▓íµ£ëÕÅ»õ╗Ñ¥~ûþ¿ïþÜäµò░Õ¡ªµû╣µ│òÒÇéÞ┐ÿµ£ëõ©Çõ©¬Õø░µâæþÜäÚù«Úóÿ׫▒µÿ»Õ«ÊÄûÑÕăþÉåÕÆîmobiusÕÅìµ╝öþÜäÕà│¥p╗´╝îÚéúõ©¬Õ£░µû╣ÕÑ¢µÖªµÂ®ÒÇéÒÇ?br>ÒÇÇÒÇÇÞÀƒµÄÆÕêùþ╗äÕÉêþø©Õà│þÜäÿqÿµ£ë׫▒µÿ»þöƒµêɵÄÆÕêùÕÆîþ╗äÕÉêÒÇéþöƒµêɵÄÆÕêùÕê®þö¿Úéúõ©¬õ╗Çõ╣êÕ¡ùÕà©Õ║ŵ│òÕÑ¢ÕâÅÞâ÷Õñƒõ║åÕQîþ╝û¢EïÕÑ¢Õ«×þÄ░ÒÇéþöƒµêÉþ╗äÕÉêµû╣µ│òþ▒╗õ╝╣{Ç?br>
2.õ║îÚí╣Õ╝ÅÕ«ÜþÉ?br>µ£ëÕ¥êÕñÜÕà¼Õ╝Å´╝îþö¿þÜäµùÂÕÇÖÕÅ»õ╗ÑþÄ░µƒÑÒÇéþ╗êõ║ÄþƒÑÚüôõ║åõ©ëÞºÆÕ¢óµò░ÕăµØÑÞÀƒµÄÆÕêùþ╗äÕÉêµ£ëÕà╗I╝îÞÇîõ©öµÿ»õ©Çõ©¬Õ¥ê¢ÄÇïzüþÜäÕà¼Õ╝ÅÒÇ?br>Õ¥êÕñÜÕà¼Õ╝ÅþÜäµÄ¿Õ»╝þö¿þÜäµÇصâ│Õ¥êÕªÖÒÇéµ£ëõ©Çõ©¬Õ¥êÕÑ¢þÜäµÇصâ│׫▒µÿ»µè?1 + x) ^ nÕê®þö¿õ║îÚí╣Õ╝ÅÕ«ÜþÉåÕ▒òÕ╝ÇÕQîþäÂÕÉĵ▒éÕ»╣{Çüµ▒é┐U»ÕêåÕQîÕ▒àþäÂÕÅ»õ╗ÑÕ»╝Õç║Õ¥êÕñÜõ©ìÕÅ»µÇØÞ««þÜäÕà¼Õ╝ÅÒÇ?br>ÿqÿµ£ëõ©Çõ©¬Õ¥êÚçìÞªüþÜäÕ«ÜþÉåÕ░▒µÿ»pascalÕ«ÜþÉåÕQîpascalÚÇƵĿÕ╝Åե굣ëþö¿ÕQêÕ▒òÕ╝ÇÕÉĵ£ëõ©ñþºìÕ¢óÕ╝ÅÕQîõ©Ç┐Uìµÿ»õ©èõ©ïÚÖÉÕØçõ©ìÕ«ÜÕQîõ©Ç┐Uìµÿ»õ©ïÚÖÉõ©ìÕ«ÜÕQë´╝îÕÅ»õ╗ÑÞºúÕå│Õ¥êÕñÜ¥läÕÉêµò░þÜäµ▒éÕÆîÚù«ÚóÿÒÇ?br>ÕŪÕñûõ©Çõ©¬ÚçìÞªüþÜäÕ«ÜþÉå׫▒µÿ»þëøÚí┐õ║îÚí╣Õ╝ÅÕ«ÜþÉå´╝îÕ£¿þöƒµêÉÕ碵ò¯C©¡Õ║öþö¿‗q┐µ│øÕQîÕŻ׫▒µÿ»µÄ¿Õ»╝ÞÁõhØѵ£ëþé╣¥JüÒÇ?br>
3.ÚÇƵĿÕà│þ│╗ÕÆîþöƒµêÉÕ碵ò?br>ÒÇÇÒÇǵ▒éÞºú¥U┐µÇºÚÇƵĿÕà│þ│╗þÜäþë╣Õ¥üµû╣¢EïþÜäµûÊÄ│òÿqÿµÿ»µ£ëõ©ÇÕ«Üõ¡hÕÇ╝þÜäÕQîõ¢åµÿ»þ╝û¢Eïõ©ìÚÇéþö¿ÒÇénÞºúþ║┐µÇºÚ¢ÉïãíÚÇƵĿµû╣þ¿ïµ£ëþƒ®ÚÿÁÞºúµ│òÒÇéþ¿ìÕ¥«ÕñìµØéþé╣þÜäÚÇƵĿÕà│þ│╗ÕQêÚØ×¥U┐µÇº´╝ëÕQîþë╣Õ¥üµû╣¢EïÕ░▒õ©ìÕñƒþö¿õ║åÕQîÕ┐àÖÕ╚ØÑ¡Õç║þöƒµêÉÕ碵ò░Þ┐Öõ©¬µ£ëÕèøþÜ䵡ªÕÖ¿ÒÇéµäƒÞºëþöƒµêÉÕ碵ò░Õ«×Õ£¿µÿ»Õñ¬õ╝ÿ¥ƒÄÒÇüÕñ¬Õ╝║Õñºõ║åÒÇéþöƒµêÉÕ碵ò░þÜäÕà│Úö«×«▒µÿ»ÞªüµèèÕñÜÚí╣Õ╝ŵïåÕêåµêÉ(1-rx)^nÿqÖþºìÕ¢óÕ╝ÅÕQîÞ┐ÖµáÀÕ░▒ÕÅ»õ╗ÑÕê®þö¿þëøÚí┐õ║îÚí╣Õ╝ÅÕ«ÜþÉåÕ▒òÕ╝Çõ║åÒÇ?br>ÒÇÇÒÇÇÕ£¿þë╣îDèÞ«íµò░Õ║ÅÕêùÚçîÚØóµÅÉÕê¯C║åþøÆÞúàþÉâÚù«ÚóÿÒÇéÕ░åpõ©¬õ©ìÕÉîþÜäþÉâµö¥ÕàÑkõ©¬þø©ÕÉîþÜäþøÆÕ¡ÉÕQêµ»Åõ©¬þøÆÕ¡ÉÚØ×¢I║´╝ëþÜäµû╣µ│òµò░µÿ»þ¼¼õ║îþ▒╗Stirlingµò░S(p, k)ÕQøÕ░åpõ©¬þø©ÕÉîþÜäþÉâµö¥ÕàÑkõ©¬þø©ÕÉîþÜäþøÆÕ¡ÉÕQêµ»Åõ©¬þøÆÕ¡ÉÚØ×¢I║´╝ëþÜäµû╣µ│òµò░µÿ»Õêåµïåµò░ÕQîÕÅ»õ╗ÑբƥlôõÏôµò┤µò░ÕêÆÕêåÚù«ÚóÿÕQîþö¿Õ迵ÇüÞºäÕêƵ▒éÞºú´╝ø׫åpõ©¬õ©ìÕÉîþÜäþøÆաɵöæÍàÑõ©ìÕÉîþÜäkõ©¬þøÆÕ¡ÉÕãêõ©öµ»Åõ©¬ÚØ×¢I║þÜäµûÊÄ│òµò¯CÏôk! * S(p, k)ÒÇ?br>ÒÇÇÒÇǵ£ëÕçáõ©¬Õ¥ê¥lÅÕà©þÜäÚÇƵĿÕà│þ│╗ÕQܵûɵ│óÚéúÕÑæµò░ÕêùÒÇüCatalanµòÄ═╝êÕçáþºì¥lÅÕà©þÜäÕ┼×Õ╝Å´╝Üõ©ëÞºÆÕëûÕêåµò░ÒÇüõ║îÕÅëþöƒµêɵáæõ©¬µò░ÒÇ?1-1Õ║ÅÕêùÒÇüÕèáµï¼ÕÅÀÕ║ÅÕêù¢{ëþ¡ëÕQëÒÇüStirlingµòÄ═╝êõ©ñþºìÕQîþ¼¼õ║îþºìµ»öÞ¥âÕ©©þö¿ÕQëÒÇüµ▒ëÞ»║ÕíöÒÇünõ©¬Õ£åÕêçÕë▓‗q│ÚØóµò░ÒÇünµØíþø┤¥U┐kõ©¬õ║ñþé╣ÕêçÕë▓ÕÒ^ÚØóµò░¢{ëþ¡ëÒÇ鵡ñÕñû´╝îµáãDÁ\Õ¥äõ©¡µÅÉÕê░þÜäÕÒ^┐UàRÇüÕÅì׫äÕÆîõ©Çõ©ÇÕ»╣Õ║öÿqÖõ©ë┐UìÕêåµ×ÉÚù«ÚóÿþÜäµûÊÄ│òõ╣ƒÕ¥êÕÇ╝Õ¥ùÕǃÚë┤ÒÇ?br>
4.polyaÕ«ÜþÉå µ»öÞ¥âÕñìµØéÕQîÞ┐çõ©ÇÚÿÁÕ¡ÉÕÑ¢ÕÑ¢µÇ╚Ø╗ôõ©ïÒÇ?img src ="http://m.shnenglu.com/sdfond/aggbug/81808.html" width = "1" height = "1" />
sdfond 2009-05-04 09:17 ÕÅæÞí¿Þ»äÞ«║
]]>sdfond 2009-04-30 09:12 ÕÅæÞí¿Þ»äÞ«║
]]>#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010;
struct Node
{
int v, id;
};
Node arr[N];
bool cmp(const Node &n1, const Node &n2)
{
return n1.v < n2.v;
}
int main()
{
int n, mine, cnt, pos, tol, ans, tmp, mini;
bool tag[N];
while (scanf("%d", &n) == 1)
{
mini = 0x3fffffff;
memset(tag, 0, sizeof(tag));
for (int i = 0; i < n; i++)
{
scanf("%d", &arr[i].v);
mini <?= arr[i].v;
arr[i].id = i;
}
sort(arr, arr + n, cmp);
ans = 0;
for (int i = 0; i < n; i++)
{
if (tag[i])
continue;
if (i == arr[i].id)
continue;
pos = i;
mine = arr[i].v;
cnt = 0;
tol = mine;
while (arr[pos].id != i)
{
cnt++;
pos = arr[pos].id;
tag[pos] = 1;
tol += arr[pos].v;
mine <?= arr[pos].v;
}
tmp = tol + (cnt - 1) * mine;
tmp <?= tol + mine + (cnt + 2) * mini;
ans += tmp;
}
printf("%d\n", ans);
}
return 0;
}
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010;
struct Node
{
int v, id;
};
Node arr[N];
bool cmp(const Node &n1, const Node &n2)
{
return n1.v < n2.v;
}
int main()
{
int n, mine, cnt, pos, tol, ans, tmp, mini;
bool tag[N];
while (scanf("%d", &n) == 1)
{
mini = 0x3fffffff;
memset(tag, 0, sizeof(tag));
for (int i = 0; i < n; i++)
{
scanf("%d", &arr[i].v);
mini <?= arr[i].v;
arr[i].id = i;
}
sort(arr, arr + n, cmp);
ans = 0;
for (int i = 0; i < n; i++)
{
if (tag[i])
continue;
if (i == arr[i].id)
continue;
pos = i;
mine = arr[i].v;
cnt = 0;
tol = mine;
while (arr[pos].id != i)
{
cnt++;
pos = arr[pos].id;
tag[pos] = 1;
tol += arr[pos].v;
mine <?= arr[pos].v;
}
tmp = tol + (cnt - 1) * mine;
tmp <?= tol + mine + (cnt + 2) * mini;
ans += tmp;
}
printf("%d\n", ans);
}
return 0;
}
sdfond 2009-04-17 09:05 ÕÅæÞí¿Þ»äÞ«║
]]>