群結(jié)構(gòu)
定理1：若G為一個循環(huán)群，則G內(nèi)每個滿足ord(
α)=s的元素
α都是擁有s個元素的循環(huán)子群的生成元
證明：
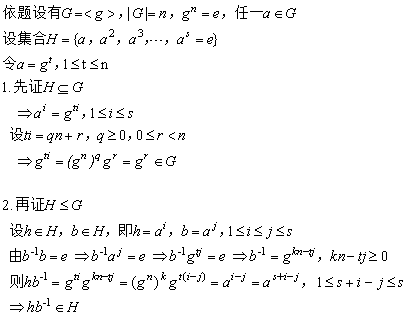
定理2：若G為一個階為n的有限循環(huán)群，g為對應(yīng)的生成元，則對整除n的每個整數(shù)k，G都存在一個唯一的階為k的循環(huán)子群H。
這個子群是由g
n/k生成的。H是由G內(nèi)滿足條件
αk=1的元素組成的，且G不存在其它子群
證明：
推論：從上述兩定理可知有限循環(huán)群、子群及生成元的關(guān)系如下
例子：依據(jù)上述推論得如下
生成元判定算法
輸入：循環(huán)群G、某子群的階k
1）若k=1，則直接輸出e。否則轉(zhuǎn)到2）
2）隨機從G-{e}中選擇一元素x
3）若x
k≠e，則轉(zhuǎn)回2）。否則若k為素數(shù)，則跳到5）；若k為合數(shù)，則轉(zhuǎn)到4）
4）遍歷整除k的真因子d，若x
d=e，則轉(zhuǎn)回2）
5）輸出x
posted on 2024-03-20 22:49
春秋十二月 閱讀(681)
評論(0) 編輯 收藏 引用 所屬分類:
Algorithm