Bellman-Ford算法與另一個非常著名的Dijkstra算法一樣,用于求解單源點最短路徑問題。Bellman-ford算法除了可求解邊權均非負的問題外,還可以解決存在負權邊的問題(意義是什么,好好思考),而Dijkstra算法只能處理邊權非負的問題,因此 Bellman-Ford算法的適用面要廣泛一些。但是,原始的Bellman-Ford算法時間復雜度為 O(VE),比Dijkstra算法的時間復雜度高,所以常常被眾多的大學算法教科書所忽略,就連經典的《算法導論》也只介紹了基本的Bellman-Ford算法,在國內常見的基本信息學奧賽教材中也均未提及,因此該算法的知名度與被掌握度都不如Dijkstra算法。事實上,有多種形式的Bellman-Ford算法的優化實現。這些優化實現在時間效率上得到相當提升,例如近一兩年被熱捧的SPFA(Shortest-Path Faster Algoithm 更快的最短路徑算法)算法的時間效率甚至由于Dijkstra算法,因此成為信息學奧賽選手經常討論的話題。然而,限于資料匱乏,有關Bellman-Ford算法的諸多問題常常困擾奧賽選手。如:該算法值得掌握么?怎樣用編程語言具體實現?有哪些優化?與SPFA算法有關系么?本文試圖對Bellman-Ford算法做一個比較全面的介紹。給出幾種實現程序,從理論和實測兩方面分析他們的時間復雜度,供大家在備戰省選和后續的noi時參考。
Bellman-Ford算法思想
Bellman-Ford算法能在更普遍的情況下(存在負權邊)解決單源點最短路徑問題。對于給定的帶權(有向或無向)圖 G=(V,E),其源點為s,加權函數 w是 邊集 E 的映射。對圖G運行Bellman-Ford算法的結果是一個布爾值,表明圖中是否存在著一個從源點s可達的負權回路。若不存在這樣的回路,算法將給出從源點s到 圖G的任意頂點v的最短路徑d[v]。
Bellman-Ford算法流程分為三個階段:
(1) 初始化:將除源點外的所有頂點的最短距離估計值 d[v] ←+∞, d[s] ←0;
(2) 迭代求解:反復對邊集E中的每條邊進行松弛操作,使得頂點集V中的每個頂點v的最短距離估計值逐步逼近其最短距離;(運行|v|-1次)
(3) 檢驗負權回路:判斷邊集E中的每一條邊的兩個端點是否收斂。如果存在未收斂的頂點,則算法返回false,表明問題無解;否則算法返回true,并且從源點可達的頂點v的最短距離保存在 d[v]中。
算法描述如下:
1 G:圖G
2 E(G):邊的集合
3 S: 源頂點
4 Dis[i]:表示s到i的最短距離,初始為+∞
5 D[s]=0;
6 for (int i=0;i<|v|-1;i++)
7 for each (u,v)∈E(G)
8 if(dis[u]+w(u,v)<dis[v]
9 dis[v]=dis[u]+w(u,v);
10 for each (u,v)∈E(G)
11 if(d[v]>d[u]+w(u,v)
12 return false;//返回false,說明存在負權回路
13 return true;
14
下面給出描述性證明:
首先指出,圖的任意一條最短路徑既不能包含負權回路,也不會包含正權回路,因此它最多包含|v|-1條邊。
其次,從源點s可達的所有頂點如果 存在最短路徑,則這些最短路徑構成一個以s為根的最短路徑樹。Bellman-Ford算法的迭代松弛操作,實際上就是按頂點距離s的層次,逐層生成這棵最短路徑樹的過程。
在對每條邊進行1遍松弛的時候,生成了從s出發,層次至多為1的那些樹枝。也就是說,找到了與s至多有1條邊相聯的那些頂點的最短路徑;對每條邊進行第2遍松弛的時候,生成了第2層次的樹枝,就是說找到了經過2條邊相連的那些頂點的最短路徑……。因為最短路徑最多只包含|v|-1 條邊,所以,只需要循環|v|-1 次。
每實施一次松弛操作,最短路徑樹上就會有一層頂點達到其最短距離,此后這層頂點的最短距離值就會一直保持不變,不再受后續松弛操作的影響。(但是,每次還要判斷松弛,這里浪費了大量的時間,怎么優化?單純的優化是否可行?)
如果沒有負權回路,由于最短路徑樹的高度最多只能是|v|-1,所以最多經過|v|-1遍松弛操作后,所有從s可達的頂點必將求出最短距離。如果 d[v]仍保持 +∞,則表明從s到v不可達。
如果有負權回路,那么第 |v|-1 遍松弛操作仍然會成功,這時,負權回路上的頂點不會收斂。
Bellman-Ford的隊列實現SPFA
算法大致流程是用一個隊列來進行維護。初始時將源加入隊列。每次從隊列中取出一個元素,并對所有與他相鄰的點進行松弛,若某個相鄰的點松弛成功,則將其入隊。直到隊列為空時算法結束。
這個算法,簡單的說就是隊列優化的bellman-ford,利用了每個點不會更新次數太多的特點發明的此算法
SPFA——Shortest Path Faster Algorithm,它可以在O(kE)的時間復雜度內求出源點到其他所有點的最短路徑,可以處理負邊。SPFA的實現甚至比Dijkstra或者Bellman_Ford還要簡單:
設Dist代表S到I點的當前最短距離,Fa代表S到I的當前最短路徑中I點之前的一個點的編號。開始時Dist全部為+∞,只有Dist[S]=0,Fa全部為0。
維護一個隊列,里面存放所有需要進行迭代的點。初始時隊列中只有一個點S。用一個布爾數組記錄每個點是否處在隊列中。
每次迭代,取出隊頭的點v,依次枚舉從v出發的邊v->u,設邊的長度為len,判斷Dist[v]+len是否小于Dist[u],若小于則改進Dist[u],將Fa[u]記為v,并且由于S到u的最短距離變小了,有可能u可以改進其它的點,所以若u不在隊列中,就將它放入隊尾。這樣一直迭代下去直到隊列變空,也就是S到所有的最短距離都確定下來,結束算法。若一個點入隊次數超過n,則有負權環。
SPFA 在形式上和寬度優先搜索非常類似,不同的是寬度優先搜索中一個點出了隊列就不可能重新進入隊列,但是SPFA中一個點可能在出隊列之后再次被放入隊列,也就是一個點改進過其它的點之后,過了一段時間可能本身被改進,于是再次用來改進其它的點,這樣反復迭代下去。設一個點用來作為迭代點對其它點進行改進的平均次數為k,有辦法證明對于通常的情況,k在2左右
1 圖G
2 隊列 queue<int> q;
3 Inque[i] 標記i是否在隊列里,初始所有為false
4 S: 源頂點
5 Dis[i]:表示s到i的最短距離,初始為+∞
6
7 Dis[s]=0;
8 q.push(s);
9 inque[s]=true;
10 while(q.size()>0)
11 {
12 Int t=q.front();
13 q.pop();
14 inque[t]=false;
15 for t’s adjacent vertex v
16 if(dis[t]+w(t,v)<dis[v])
17 {
18 Dis[v]=dis[t]+w(t,v);
19 If(!inque[v])
20 {
21 q.push(v);
22 inque[v]=true;
23 }
24 }
25
26 }
27
USACO 3.2 Sweet Butter
Sweet Butter
Greg Galperin -- 2001
Farmer John has discovered the secret to making the sweetest butter in all of Wisconsin: sugar. By placing a sugar cube out in the pastures, he knows the N (1 <= N <= 500) cows will lick it and thus will produce super-sweet butter which can be marketed at better prices. Of course, he spends the extra money on luxuries for the cows.
FJ is a sly farmer. Like Pavlov of old, he knows he can train the cows to go to a certain pasture when they hear a bell. He intends to put the sugar there and then ring the bell in the middle of the afternoon so that the evening's milking produces perfect milk.
FJ knows each cow spends her time in a given pasture (not necessarily alone). Given the pasture location of the cows and a description of the paths the connect the pastures, find the pasture in which to place the sugar cube so that the total distance walked by the cows when FJ rings the bell is minimized. FJ knows the fields are connected well enough that some solution is always possible.
PROGRAM NAME: butter
INPUT FORMAT
- Line 1: Three space-separated integers: N, the number of pastures: P (2 <= P <= 800), and the number of connecting paths: C (1 <= C <= 1,450). Cows are uniquely numbered 1..N. Pastures are uniquely numbered 1..P.
- Lines 2..N+1: Each line contains a single integer that is the pasture number in which a cow is grazing. Cow i's pasture is listed on line i+1.
- Lines N+2..N+C+1: Each line contains three space-separated integers that describe a single path that connects a pair of pastures and its length. Paths may be traversed in either direction. No pair of pastures is directly connected by more than one path. The first two integers are in the range 1..P; the third integer is in the range (1..225).
SAMPLE INPUT (file butter.in)
3 4 5
2
3
4
1 2 1
1 3 5
2 3 7
2 4 3
3 4 5
INPUT DETAILS
This diagram shows the connections geometrically:
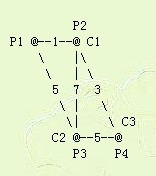
OUTPUT FORMAT
- Line 1: A single integer that is the minimum distance the cows must walk to a pasture with a sugar cube.
SAMPLE OUTPUT (file butter.out)
8
OUTPUT DETAILS:
Putting the cube in pasture 4 means: cow 1 walks 3 units; cow 2 walks 5
units; cow 3 walks 0 units -- a total of 8.
解答:
這道題直接用一般的Dijkstra算法O(P2),一共調用P次Dijkstra,總體復雜度O(P3),p=800,肯定超時,在這里用SPFA算法,O(k*c),k是2左右的常數,
調用p次,整體復雜度O(p*c*k).在0.2秒可以得出解.附原碼
/*
ID: kuramaw1
PROG: butter
LANG: C++
*/
#include <fstream>
#include <queue>
using std::ifstream;
using std::ofstream;
using std::queue;
using std::endl;
using std::vector;
#define MAX_EDGE 1451
#ifndef INT_MAX
#define INT_MAX 2147483647
#endif
struct graph
{
struct Edge
{
short n; // next adjacent edge
short v; // to which vertex
short c; // weight
Edge(const short _n=-1,const short _v=-1,const short _c=0):n(-n),v(_v),c(-c)
{
}
Edge(const Edge &e):n(e.n),v(e.v),c(e.c)
{
}
Edge & operator =(const Edge &e)
{
n=e.n;
v=e.v;
c=e.c;
return *this;
}
};
struct Ver
{
short w;
short e;//frist e
Ver(const short _w=0,const short _e=-1):w(_w),e(_e)
{
}
Ver(const Ver &v):w(v.w),e(v.e)
{
}
Ver & operator =(const Ver &v)
{
w=v.w;
e=v.e;
return *this;
}
};
typedef std::vector<Edge> EdgeSet;
typedef std::vector<Ver> VertSet;
VertSet _V;
EdgeSet _E;
// interfaces
inline void Reset(const short &n)
{
_V.resize(n);
_E.clear();
_E.reserve(MAX_EDGE);
}
inline void IncVetWei(const short &i)
{
_V[i].w++;
}
inline void InsertEdge(short u, short v, short c)
{
Edge e;
e.v = v, e.c = c, e.n = _V[u].e;
_V[u].e = _E.size();
_E.push_back(e);
e.v = u, e.c = c, e.n = _V[v].e;
_V[v].e = _E.size();
_E.push_back(e);
}
int short_dis_sum(const short &s)
{
vector<int> dis;
queue<short> q;
vector<bool> b_in_que;
dis.resize(_V.size(),INT_MAX);
b_in_que.resize(_V.size(),false);
q.push(s);
dis[s]=0;
b_in_que[s]=true;
while(q.size()>0)
{
short t=q.front();
q.pop();
b_in_que[t]=false;
short e=_V[t].e;
while(e!=-1)
{
Edge &edge=_E[e];
if(dis[t]+edge.c<dis[edge.v])
{
dis[edge.v]=dis[t]+edge.c;
if(!b_in_que[edge.v])
{
q.push(edge.v);
b_in_que[edge.v]=true;
}
}
e=edge.n;
}
}
int sum(0);
for(short i=0;i<dis.size();i++)
if(_V[i].w>0)
{
sum+=_V[i].w*dis[i];
}
return sum;
}
};
graph g;
short n,p,c;
int main()
{
ifstream in("butter.in");
in>>n>>p>>c;
g.Reset(p);
for(short i=0;i<n;i++)
{
short v;
in>>v;
g.IncVetWei(v-1);
}
for(short i=0;i<c;i++)
{
short u,v,w;
in>>u>>v>>w;
g.InsertEdge(u-1,v-1,w);
}
in.close();
int min_dis=INT_MAX;
for(int i=0;i<p;i++)
{
int dis=g.short_dis_sum(i);
if(dis<min_dis)
min_dis=dis;
}
//out
ofstream out("butter.out");
out<<min_dis<<endl;
out.close();
}
posted @
2009-08-12 21:49 kuramawzw 閱讀(1053) |
評論 (0) |
編輯 收藏
給定一個無向圖G,一條路徑經過圖G的每一條邊,且僅經過一次,這條路徑稱為歐拉路徑(Eulerian Tour),如果歐拉路徑的起始頂點和終點是同一頂點,則稱為歐拉回路(Eulerian circuit).
算法:
無向圖G存在歐拉路徑的充要條件:圖G是連通的,且至多除兩個點外(可以為0個,連接圖不可能有且僅有一個頂點的度為奇數)其它所有頂點的度為偶數.
無向圖G存在歐拉回路的充要條件:圖G是連通的且所有頂點的度為偶數;
算法描述:
1 tour: 數組,用于存儲歐拉路徑,反序輸出即為歐拉路徑
2 pos: int
3
find_eulerian_circuit()
4 {
5 pos=0;
6 find_circuit(1);
7 }
8
find_eulerian_tour()
9 {
10 find a vertex i ,the degree of which is odd
11 pos=0;
12 find_circuit(i);
13 }
14
find_circuit(vertex i)
15 {
16 while(exist j,(i,j) is the edge of G)
17 {
18 remove edge(i,j);
19 find_circuit(j);
20 }
21 tour[pos++]=i;
22 }
23
USACO 3.2 Riding the fence,就是一個求歐拉路徑的問題.
問題描述:
Farmer John owns a large number of fences that must be repaired annually. He traverses the fences by riding a horse along each and every one of them (and nowhere else) and fixing the broken parts.
Farmer John is as lazy as the next farmer and hates to ride the same fence twice. Your program must read in a description of a network of fences and tell Farmer John a path to traverse each fence length exactly once, if possible. Farmer J can, if he wishes, start and finish at any fence intersection.
Every fence connects two fence intersections, which are numbered inclusively from 1 through 500 (though some farms have far fewer than 500 intersections). Any number of fences (>=1) can meet at a fence intersection. It is always possible to ride from any fence to any other fence (i.e., all fences are "connected").
Your program must output the path of intersections that, if interpreted as a base 500 number, would have the smallest magnitude.
There will always be at least one solution for each set of input data supplied to your program for testing.
PROGRAM NAME: fence
INPUT FORMAT
|
Line 1:
|
The number of fences, F (1 <= F <= 1024)
|
|
Line 2..F+1:
|
A pair of integers (1 <= i,j <= 500) that tell which pair of intersections this fence connects.
|
SAMPLE INPUT (file fence.in)
9
1 2
2 3
3 4
4 2
4 5
2 5
5 6
5 7
4 6
OUTPUT FORMAT
The output consists of F+1 lines, each containing a single integer. Print the number of the starting intersection on the first line, the next intersection's number on the next line, and so on, until the final intersection on the last line. There might be many possible answers to any given input set, but only one is ordered correctly.
SAMPLE OUTPUT (file fence.out)
1
2
3
4
2
5
4
6
5
7
解答:簡單的歐拉路徑問題,圖采用鄰接表存儲,附原碼
/*
ID: kuramaw1
PROG: fence
LANG: C++
*/
#include <fstream>
using std::ifstream;
using std::ofstream;
using std::endl;
#ifdef _DEBUG
#include <iostream>
using std::cout;
#endif
#define MAX_V 500
#define MAX_EDGE 1025
#define MAX(a,b) ((a)>(b)?(a):(b))
struct grapha
{
struct node
{
short v;
node * next;
node(const short _v=-1):v(_v),next(NULL)
{
}
};
struct ver
{
node * r;
short d;//degree
ver():d(0)
{
r=new node();
}
~ver()
{
node * n=r;
while(n!=NULL)
{
node * t=n;
n=n->next;
delete t;
}
}
inline void add_neighbor(const short &v)
{
node * t=new node(v);
node * p=r;
node * n=p->next;
while(n!=NULL && v>n->v)
{
p=n;
n=n->next;
}
p->next=t;
t->next=n;
d++;
}
inline void remove_neighbor(const short &v)
{
node * p=r;
node * n=p->next;
while(n!=NULL && v!=n->v)
{
p=n;
n=n->next;
}
if(n!=NULL)
{
p->next=n->next;
delete n;
d--;
}
}
};
ver v[MAX_V];
short n;
short * tour;
short pos;
grapha():n(0),tour(NULL)
{
}
void add_edge(const short &_u,const short &_v)
{
v[_u-1].add_neighbor(_v-1);
v[_v-1].add_neighbor(_u-1);
short t=MAX(_u,_v);
if(t>n)
n=t;
}
void find_tour(const short &s)
{
while(v[s].d>0)
{
short j=v[s].r->next->v;
v[s].remove_neighbor(j);
v[j].remove_neighbor(s);
find_tour(j);
}
tour[pos++]=s+1;
}
void Eulerian_tour(short * _tour)
{
tour=_tour;
pos=0;
bool b=false;
for(int i=0;i<n;i++)
if(v[i].d % 2!=0)
{
find_tour(i);
b=true;
break;
}
if(!b)
find_tour(0);
}
};
grapha g;
short tour[MAX_EDGE];
short f;
int main()
{
ifstream in("fence.in");
in>>f;
for(short i=0;i<f;i++)
{
short u,v;
in>>u>>v;
g.add_edge(u,v);
}
//do
g.Eulerian_tour(tour);
//out
ofstream out("fence.out");
for(int i=f;i>=0;i--)
out<<tour[i]<<endl;
out.close();
}
posted @
2009-08-12 21:18 kuramawzw 閱讀(615) |
評論 (0) |
編輯 收藏