樹狀數組（Fenwick tree，又名binary indexed tree），是一種很實用的數據結構。它通過用節點i，記錄數組下標在[ i –2^k + 1, i]這段區間的所有數的信息（其中，k為i的二進制表示中末尾0的個數，設lowbit(i) = 2^k），實現在O(lg n) 時間內對數組數據的查找和更新。
樹狀數組的傳統解釋圖，不能很直觀的看出其所能進行的更新和查詢操作。其最主要的操作函數lowbit(k)與數的二進制表示相關，本質上仍是一種二分。因而可以通過二叉樹，對其進行分析。事實上，從二叉樹圖，我們對它所能進行的操作和不能進行的操作一目了然。
和前面提到的點樹類似，先畫一棵二叉樹，然后對節點中序遍歷（點樹是采用廣度優先），每個節點仍然只記錄左子樹信息，見圖：
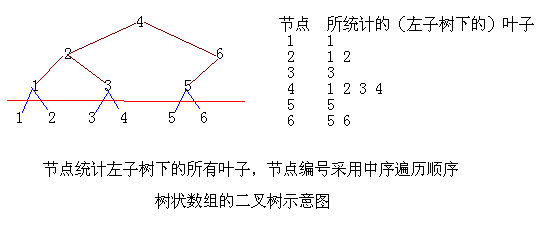
由于采用的是中序遍歷，從節點1到節點k時，剛好有k個葉子被統計。
可以證明：
葉子k，一定在節點k的左子樹下。
以節點k為根的樹，其左子樹共有葉子lowbit(k)
節點k的父節點是：k + lowbit(k) 或 k - lowbit(k)
節點k + lowbit(k) 是節點k的最近父節點，且節點k在它的左子樹下。
節點k - lowbit(k) 是節點k的最近父節點，且節點k在它的右子樹下。
節點k，統計的葉子范圍為：(k - lowbit(k), k]。
節點k的左孩子是：k - lowbit(k) / 2
下面分析樹狀數組兩面主要應用：
1 更新數據x，進行區間查詢。
2 更新區間，查詢某個數。
由于，樹狀數組只統計了左子樹的信息，因而只能查詢更新區間[1, x]。只在在滿足[x,y]的信息可以由[1,x-1]和[1,y]的信息推導出時，才能進行區間[x,y]的查詢更新。這也是樹狀數組不能用于任意區間求最值的根本原因。
先定義兩個集合：
up_right(k) ： 節點k所有的父節點，且節點k在它們的左子樹下。
up_left(k) ： 節點k所有的父節點，且節點k在它們的右子樹下。
1 更新數據x，查詢區間[1,y]。
顯然，更新葉子x，要找出葉子x在哪些節點的左子樹下。因而節點k、所有的up_right(k)
都要更新。
查詢[1, y]，實際上就是把該區間拆分成一系列小區間，并找出統計這些區間的節點?？梢酝ㄟ^找出y在哪些節點的右子樹下，這些節點恰好不重復的統計了區間[1, y-1]。因而要訪問節點y、所有的up_left(y)。
2 更新區間[1,y]，查詢數據x
這和前面的操作恰好相反。與前面的最大不同之處在于：節點保存的不再是其葉子總個數這些信息，而是該區間的所有葉子都改變了多少。也就是說：每個葉子的信息，分散到了所有對它統計的節點上。因此操作和前面相似：
更新[1,y]時，更新節點y、所有up_left(y)。
查詢x時， 訪問x、所有up_right(x)。
前面的樹狀數組，只對左子樹信息進行統計，如果從后往前讀數據初始化樹狀數組，則變成只對右子樹信息進行統計，這時更新和查詢操作，剛好和前面的相反。
一般情況下，樹狀數組比點樹省空間，對區間[1, M]只要M+1空間，查詢更新時定位節點比較快，定位父節點和左右孩子相對麻煩點（不過，一般也不用到。從上往下查找，可參考下面代碼中的erease_nth函數（刪除第n小的數））。
下面是使用樹狀數組的實現代碼（求逆序數和模擬約瑟夫環問題）：
樹狀數組
//www.cnblogs.com/flyinghearts
#include<cstdio>
#include<cstring>
#include<cassert>
template<int N> struct Round2k
{ enum { down = Round2k<N / 2u>::down * 2}; };
template<> struct Round2k<1> { enum { down = 1}; };
template <int Total, typename T = int> //區間[1, Total]
class BIT {
enum { Min2k = Round2k<Total>::down};
T info[Total + 1];
T sz; //可以用info[0]儲存總大小
public:
BIT() { clear(); }
void clear() { memset(this, 0, sizeof(*this));}
int size() { return sz; }
int lowbit(int idx) { return idx & -idx;}
//尋找最近的父節點，left_up/right_up 分別使得idx在其右/左子樹下
void left_up(int& idx) { idx -= lowbit(idx); }
void right_up(int& idx) { idx += lowbit(idx); }
void update(int idx ,const int val = 1) { //葉子idx 改變val個
assert(idx > 0);
sz += val;
for (; idx <= Total; right_up(idx)) info[idx] += val;
}
void init(int arr[], int n) { // arr[i]為葉子i+1的個數
assert(n <= Total);
sz = n;
// for (int i = 0; i < n; ) {
// info[i + 1] = arr[i];
// if (++i >= n) break;
// info[i + 1] = arr[i];
// ++i;
// for (int j = 1; j < lowbit(i); j *= 2u) info[i] += info[i - j];
// }
for (int i = 0; i < n; ) {
info[i + 1] = arr[i];
if (++i >= n) break;
int sum = arr[i];
int pr = ++i;
left_up(pr);
for (int j = i - 1; j > pr; left_up(j)) sum += info[j];
info[i] = sum;
}
}
int count(int idx) { //[1,idx] - [1, idx-1]
assert(idx > 0);
int sum = info[idx];
// int pr = idx; //int pr = idx - lowbit(idx);
// left_up(pr);
// for (--idx; idx > pr; left_up(idx)) sum -= info[idx]; //
// return sum;
for (int j = 1; j < lowbit(idx); j *= 2u) sum -= info[idx - j];
return sum;
}
int lteq(int idx) { //小等于
assert(idx >= 1 && idx <= Total);
int sum = 0;
for (; idx > 0; left_up(idx)) sum += info[idx];
return sum;
}
int gt(int idx) { return sz - lteq(idx); } //大于
int operator[](int n) { return erase_nth(n, 0); } //第n小
int erase_nth(int n, const bool erase_flag = true) //刪除第n小的數
{
assert(n >=1 && n <= sz);
sz -= erase_flag;
int idx = Min2k; //從上往下搜索，先定位根節點
for (int k = idx / 2u; k > 0; k /= 2u) {
int t = info[idx];
if (n <= info[idx]) { info[idx] -= erase_flag; idx -= k;} //進入左子樹
else {
n -= t;
if (Total != Min2k && Total != Min2k - 1) //若不是完全二叉樹
while (idx + k > Total) k /= 2u; //則必須計算右孩子的編號
idx += k; //進入右子樹
}
}
assert(idx % 2u); //最底層節點m一定是奇數，有兩個葉子m，m+1
if (n > info[idx]) return idx + 1; //節點m+1前面已經更新過
info[idx] -= erase_flag;
return idx;
}
void show()
{
for (int i = 1; i <= Total; ++i)
if (count(i)) printf("%2d ", i);
printf("\n");
}
};
void ring() //約瑟夫環
{
const int N = 17; //N個人編號：1,2, N
const int M = 7; //報數：1到M，報到M的出列
printf(" N: %d M: %d\n", N, M);
BIT<N> pt;
// for (int i = 0; i < N; ++i) pt.update(i + 1);
int arr[N];
for (int i = 0; i < N; ++i) arr[i] = 1;
pt.init(arr, N);
for (int j = N, k = 0; j >= 1; --j) {
k = (k + M-1) % j;
int t = pt.erase_nth(k + 1);
printf(" turn: %2d out: %2d rest: ", N - j, t);
pt.show();
}
printf(" \n\n");
}
int ra(int arr[], int len) //求逆序數-直接搜索
{
int sum = 0;
for (int i = 0; i < len - 1; ++i)
for (int j = i + 1; j < len; ++j)
if (arr[i] > arr[j]) ++sum;
return sum;
}
template<int N>
int rb(int arr[], int len) //求逆序數-使用樹狀數組
{
BIT<N> pt;
int sum = 0;
for (int i = 0; i < len; ++i) {
pt.update(arr[i] + 1);
sum += pt.gt(arr[i] + 1);
}
return sum;
}
int main()
{
int arr[] = { 4,3,2,1,0,5, 1,3,0,2};
const int N = sizeof(arr) / sizeof(arr[0]);
printf("%d %d\n\n", ra(arr, N), rb<6>(arr, N));
ring();
}
作者： flyinghearts
出處： http://www.cnblogs.com/flyinghearts/
本文采用知識共享署名-非商業性使用-相同方式共享 2.5 中國大陸許可協議進行許可，歡迎轉載，但未經作者同意必須保留此段聲明，且在文章頁面明顯位置給出原文連接，否則保留追究法律責任的權利。