Posted on 2008-10-13 18:45
路緣 閱讀(2146)
評論(2) 編輯 收藏 引用 所屬分類:
計算機圖形學
作者：路緣
原文網址：http://www.cnblogs.com/xuyuan77/archive/2008/10/13/1310269.html
德國數學家David Hilbert發現了一種曲線，首先把一個正方形等分成四個小正方形，依次從西南角的正方形中心出發往北到西北正方形中心，再往東到東北角的正方形中心，再往南到東南角正方形中心，這是一次迭代，如果對四個小正方形繼續上述過程，往下劃分，反復進行，最終就得到一條可以填滿整個正方形的曲線，這就是Hibert曲線，其大致過程如下圖所示
Hibert曲線生成過程
下面我們來看如何寫程序生成這樣的曲線，其實不管迭代多少次，都是由如下的圖形
基本圖
構成，唯一所不同的是開口方向不一樣。開口方向不一樣就涉及到圖像旋轉，圖像旋轉的基本知識接下來會介紹。目前我們最關心的是這樣生成的曲線過程右什么規律，從上述描述生成的過程就已經看出了規律，當然人肯定一眼就看出來了，但計算機如何知道呢？這就是生成Hibert曲線算法的關鍵了：
為了便于找出規律，我們來看下面一副圖
上圖中應該是把所有開口方向（共四種）都涵蓋了。我們約定四種類型：
開口往南－0，開口往西－1，開口往北－2，開口往東－3。我們結合基本圖，就有這樣的規律，畫表如下：
|
點
|
點所在圖類型
|
以該點為中心產生的圖類型
|
|
dot1
|
0
|
1
|
|
dot1
|
1
|
2
|
|
dot1
|
2
|
3
|
|
dot1
|
3
|
0
|
其他的點類似也有類似的規律，這個規律才是我們編碼的基礎。是下次遞歸調用畫圖函數傳參數的前提。下面我們來看一下畫圖中涉及到的圖像旋轉的相關數學知識。
圖像旋轉
圖像旋轉是指把定義的圖像繞某一點以逆時針或順時針方向旋轉一定的角度，通常是指繞圖像的中心以逆時針方向旋轉。
假設圖像的左上角為（left, top),右下角為（right, bottom)，則圖像上任意點（x0, y0）繞其中心（xcenter, ycenter)逆時針旋轉angle角度后，新的坐標位置（x′, y′）的計算公式為：
xcenter = (right － left ＋ 1) ／ 2 ＋ left;
ycenter = (bottom － top ＋ 1) ／ 2 ＋ top;
x′ = (x0 － xcenter) cosθ － (y0 － ycenter) sinθ ＋ xcenter;
y′ = (x0 － xcenter) sinθ ＋ (y0 － ycenter) cosθ ＋ ycenter;
與圖像的鏡像變換相類似，也采用按行逐點變換的方式實現圖像的旋轉。
現在一切都準備就緒，我們來實現相關的算法如下：
/**//**********************************************************************************************
功能：實現繪制Hilbert曲線
參數：
pDC:設備上下文
n:維都
len:邊長
x:中心橫坐標
y:中心縱坐標
iType:繪畫類型，開口：0－南，1－西，2-北，3-東
unit_length：最小單元長度
/**********************************************************************************************/
void CGraphicAppView::DrawHilbert(CDC* pDC, int n, int len, int x, int y, int iType, int unit_length)
{
//存儲以x,y為中心的西南、西北、東北、東南四角定點的坐標
int arr[4][2];
arr[0][0] = x -len/4; arr[0][1] =y+len/4;
arr[1][0] = x -len/4; arr[1][1] =y-len/4;
arr[2][0] = x +len/4; arr[2][1] =y-len/4;
arr[3][0] = x +len/4; arr[3][1] =y+len/4;
//存儲以x,y為中心的（西南、西北、東北、東南四角定點）經過處理后的坐標
int a[4][2];
memset(a, 0, sizeof(a));
int sin_v=0,cos_v=1;//默認為0度的值
switch(iType)//根據不同的開口方向，對旋轉三角函數賦值
{
case 1://開口向左
sin_v = 1; cos_v = 0;
break;
case 2://開口向上
sin_v = 0; cos_v = -1;
break;
case 3: //開口向右
sin_v = -1; cos_v = 0;
break;
}
for(int i = 0; i<4; i++)//完成旋轉
{
a[i][0] = (arr[i][0] - x)*cos_v - (arr[i][1] - y)*sin_v + x;
a[i][1] = (arr[i][0] - x)*sin_v + (arr[i][1] - y)*cos_v + y;
}
CPen newPen(PS_DASHDOTDOT, 2, RGB(y%255, x%255, (y+x)%255));
pDC->SelectObject(&newPen);
if(n > 1)
{
int length = len/2;
DrawHilbert(pDC, n-1, length, a[0][0], a[0][1], (1+iType)%4,unit_length);
DrawHilbert(pDC, n-1, length, a[1][0], a[1][1], iType,unit_length);
DrawHilbert(pDC, n-1, length, a[2][0], a[2][1], iType,unit_length);
DrawHilbert(pDC, n-1, length, a[3][0], a[3][1], (3+iType)%4,unit_length);
switch(iType)
{
case 0:
case 2:
pDC->MoveTo(x-length + 0.5*unit_length, y + 0.5*unit_length);
pDC->LineTo(x-length + 0.5*unit_length, y - 0.5*unit_length);
pDC->MoveTo(x-0.5*unit_length, y - (1-iType)*0.5*unit_length);
pDC->LineTo(x+0.5*unit_length, y - (1-iType)*0.5*unit_length);
pDC->MoveTo(x+length - 0.5*unit_length, y + 0.5*unit_length);
pDC->LineTo(x+length - 0.5*unit_length, y - 0.5*unit_length);
break;
case 1:
case 3:
pDC->MoveTo(x-0.5*unit_length, y -length + 0.5*unit_length);
pDC->LineTo(x+0.5*unit_length, y -length + 0.5*unit_length);
pDC->MoveTo(x+(2-iType)*0.5*unit_length, y - 0.5*unit_length);
pDC->LineTo(x+(2-iType)*0.5*unit_length, y + 0.5*unit_length);
pDC->MoveTo(x-0.5*unit_length, y +length - 0.5*unit_length);
pDC->LineTo(x+0.5*unit_length, y +length - 0.5*unit_length);
break;
}
}
else
{
pDC->MoveTo(a[0][0], a[0][1]);
pDC->LineTo(a[1][0], a[1][1]);
pDC->LineTo(a[2][0], a[2][1]);
pDC->LineTo(a[3][0], a[3][1]);
}
}
算法中還涉及到了，連接迭代產生的圖像的過程，由于算法不是很優雅，在這兒就不細說了，其次如果把二維映射到三維，將會得到更美妙的曲線，最近忙著找工作，有時間再想了，有興趣的朋友可以研究下三維的情況。
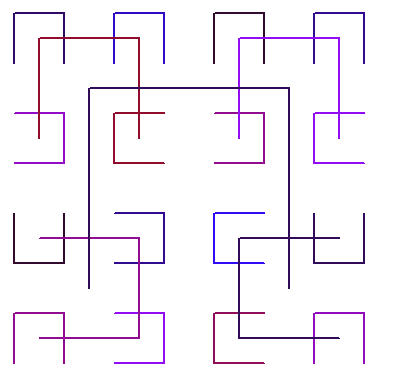
其次希望有朋友能有更好的算法，希望不吝賜教，先謝過了。最后我們來看一下迭代6次的一個運行結果圖：
調用的代碼段如下：
void CGraphicAppView::OnDraw(CDC* pDC)
{
CGraphicAppDoc* pDoc = GetDocument();
ASSERT_VALID(pDoc);
if (!pDoc)
return;
// TODO: add draw code for native data here
int n = 6;
long t = ::pow(2.0, n);
int length = 400;
int unit_length = length/t;
DrawHilbert(pDC, n, length, 200, 200, 0, unit_length);
}